
第3章解析函数的积分 By 付小宁
第3章 解析函数的积分 By 付小宁
第一节复变函数积分的概念 一、积分的定义 1.有向曲线: 设C为平面上给定的一条光滑(或按段光滑) 曲线,如果选定C的两个可能方向中的一个作 为正方向(或正向),那么我们就把C理解为带 有方向的曲线,称为有向曲线 如果A到B作为曲线C的正向, B 那么B到A就是曲线C的负向, 记为C. +x
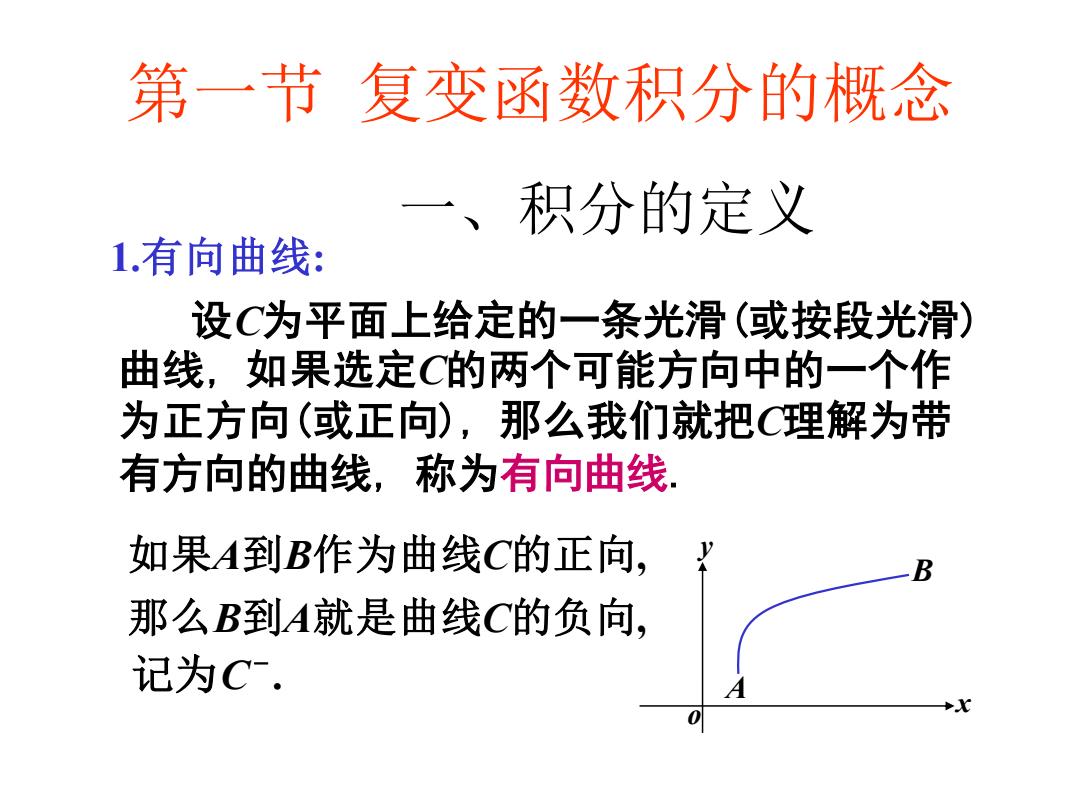
一、积分的定义 1.有向曲线: 设C为平面上给定的一条光滑(或按段光滑) 曲线, 如果选定C的两个可能方向中的一个作 为正方向(或正向), 那么我们就把C理解为带 有方向的曲线, 称为有向曲线. x y o A 如果A到B作为曲线C的正向 B , 那么B到A就是曲线C的负向, . − 记为C 第一节 复变函数积分的概念
关于曲线方向的说明: 在今后的讨论中,常把两个端点中的一个作 为起点,另一个作为终点,除特殊声明外,正方 向总是指从起点到终点的方向. 简单闭曲线正向的定义: 简单闭曲线C的正向 是指当曲线上的点P顺此方 P 向前进时,邻近P点的曲线 的内部始终位于P点的左方. 与之相反的方向就是曲线的负方向
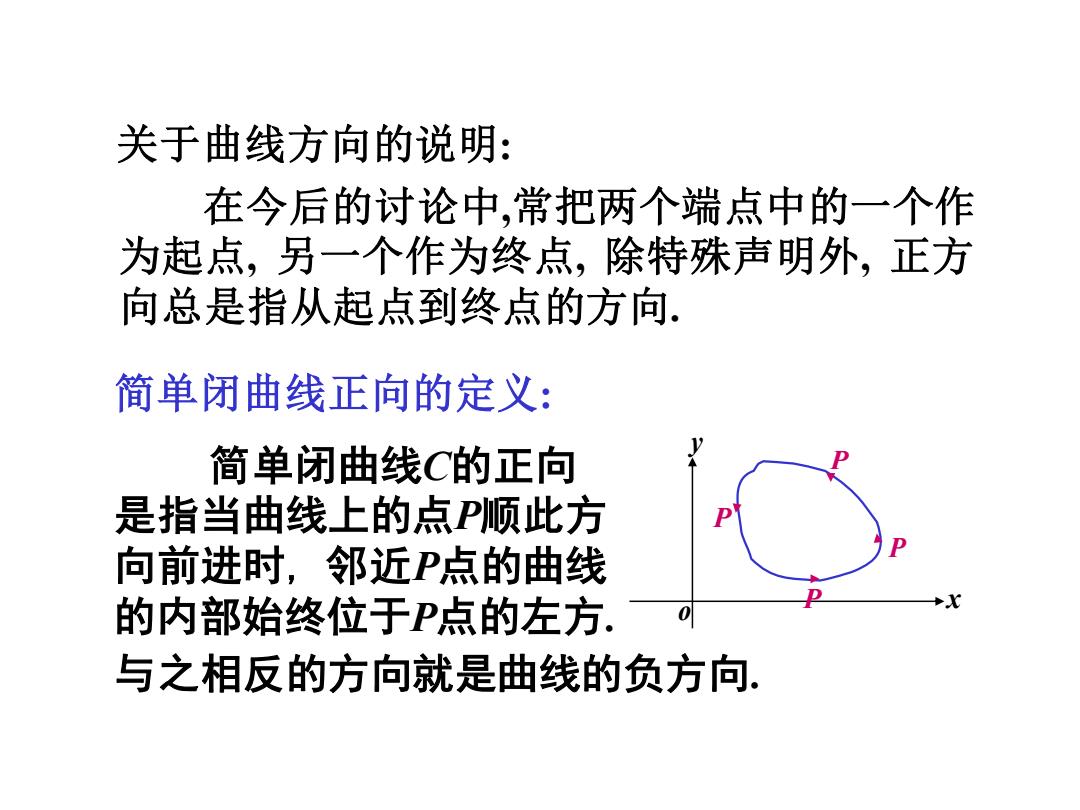
简单闭曲线正向的定义: 简单闭曲线C的正向 是指当曲线上的点P顺此方 向前进时, 邻近P点的曲线 的内部始终位于P点的左方. x y o P P P P 与之相反的方向就是曲线的负方向. 关于曲线方向的说明: 在今后的讨论中,常把两个端点中的一个作 为起点, 另一个作为终点, 除特殊声明外, 正方 向总是指从起点到终点的方向

2.积分的定义: 设在复平面C上有一条连接Z及Z两点的简 单曲线C。设z=u(x,y)十iv(x,y)是在C上的连续 函数。其中(x,y)及v(x,y)是z)的实部及虚部。 把曲线C用分点 Z0,21,22,2m-1,Zn=Z 分成n个更小的弧,在这里分点zk(k=0,1,2,,n) 是在曲线C上按从2o到Z的次序排列的。 如果马是k到k+1的弧上任意一点,那么考 虑和式 ∑f(5A21-2) k=0
设在复平面C上有一条连接 及Z两点的简 单曲线C。设f(z)=u(x,y)+iv(x,y)是在C上的连续 函数。其中u(x,y)及v(x,y)是f(z)的实部及虚部。 把曲线C用分点 分成n个更小的弧,在这里分点 是在曲线C上按从 到Z的次序排列的。 0 z 如果 是 到 的弧上任意一点,那么考 虑和式 z0 ,z1 ,z2 ...,zn−1 ,zn = Z z (k 0,1,2,...,n) k = 0 z k k+1 z k z ( )( ) 1 0 1 k n k k k f z − z − = + 2. 积分的定义:

复变函数的积分 Zn 三 Z 5 Zk C Zk-1 29 oZo
复变函数的积分 0 z 1 z k−1 z k k z zn = Z n−1 z C

复变函数的积分 分实部与虚部,有 u5,)+n5,m:JI1-,)+U-川 k=0 或 4(5,7)(xk+1-x)-∑(5,7)yk+1-yg) k=0 k=0 +∑r(5,:x1-)+另5,01-4 k=0 在这里xk、y%及5k、k分别表示的Zk与5 实部与虚部
复变函数的积分 分实部与虚部,有 或 [ ( , ) ( , )][( ) ( ) ] 1 1 0 1 k k n k k k k k k k u + iv x − x + i y − y + − = + 在这里 分别表示的 实部与虚部。 [ ( , ) ( ) ( , ) ( ), ( , ) ( ) ( , ) ( ) 1 0 1 1 0 1 1 0 1 1 0 1 − = + − = + − = + − = + + − + − − − − n k k k k k n k k k k k n k k k k k n k k k k k i v x x u y y u x x v y y k k k k x 、y 及 、 k k z 与

复变函数的积分 按照关于实变函数的线积分的结果,当曲线C 上的分点个数无穷增加,而且 max{2k+1-2k=V(xk+1-x)2+(yk+1-y)2 →0k=0,1,2,,n-1}>0 时,上面的四个式子分别有极限: [u(x.y)dx.[v(y)dy.[v(dx u()dv. 这时,我们说原和式有极限 Lu(x,y)dx-v(x,y)dy+iv(x,y)dx+u(x,y)dy
复变函数的积分 按照关于实变函数的线积分的结果,当曲线C 上的分点个数无穷增加,而且 时,上面的四个式子分别有极限: 0 | 0,1,2,..., 1} 0 max{| | ( ) ( ) 2 1 2 1 1 → = − → + − = + − + + − k n z z x x y y k k k k k k 这时,我们说原和式有极限 ( , )d , ( , )d , ( , )d , ( , )d , C C C C u x y x v x y y v x y x u x y y u(x, y)dx v(x, y)dy i v(x, y)dx u(x, y)dy, C C − + +

复变函数的积分 这个极限称为函数z)沿曲线C的积分,记为 f(z)dz. 因此,我们有 〔f(z)d正 =[u(x,y)dx-v(x.y)dy+i[v(x.y)dx+u(x.y)dy
复变函数的积分 这个极限称为函数f(z)沿曲线C的积分,记为 ( )d . C f z z 因此,我们有 ( , )d ( , )d ( , )d ( , )d , ( )d u x y x v x y y i v x y x u x y y f z z C C C = − + +

复变函数的积分 如果C是简单光滑曲线x=p(t),y=(t)t≤t≤T) ,并且t及T相应于z及Z,那么上式右边的 积分可以写成黎曼积分的形式,例如其中第一 个可以写成 p()dr 因此,我们有 f(e)d=[(o,)+i(a,o'(④)+i0'(0
复变函数的积分 如果C是简单光滑曲线: ,并且 ,那么上式右边的 积分可以写成黎曼积分的形式,例如其中第一 个可以写成 因此,我们有 ( ), ( )( ) x = t y = t t 0 t T t 0及T相应于z0及Z T t u t t 0 (,)'( )d f z z u iv t i t t T C t ( )d [ ( , ) ( , )][ '( ) '( )]d 0 = + +

复变函数的积分 我们可以看到,把dz形式地换成微分,就直接 得到上式,因此有 Lfe=fzz'灿 当是分段光滑简单曲线时,我们仍然可以得到 这些结论
复变函数的积分 我们可以看到,把dz形式地换成微分,就直接 得到上式,因此有 f z z f z t z t t T C t ( )d ( ( )) '( )d 0 = 当是分段光滑简单曲线时,我们仍然可以得到 这些结论