
上游充通大学 SHANGHAI JIAO TONG UNIVERSITY 第二章解析函数 漏 w SHANG 1日g日 ERSITY
第二章 解析函数

上游充通大学 第二章解析函数纲要 SHANGHAI JIAO TONG UNIVERSITY 1.极限和连续性 2.导数与解析函数 3.初等函数 4.解析函数和调和函数
第二章 解析函数纲要 1. 极限和连续性 2. 导数与解析函数 3. 初等函数 4. 解析函数和调和函数

上游充通大 SHANGHAI JIAO TONG UNIVERSITY §2.1极限和连续性 2.1.1极限 定义(函数的极限):设函数w=f()在00,3 δ>0(0<6≤p),使得 → 0<2-z01K6= If(2)-A|K8, 则称A为f(z)当z趋向于z时的极限,记作 lim f(z)=A 或记作当z→z时,f(2)→A
定义(函数的极限): 设函数 w = f (z) 在 0 0 (0 0, ∃ ⇒ § 2.1 极限和连续性

上游充通大 SHANGHAI JIAO TONG UNIVERSITY (E-δ)语言极限的定义 AUGUSTIN CAUCHY f(a) r789-r857 LA POSTE 1989 3,60

上游充通大学 SHANGHAI JIAO TONG UNIVERSITY §2.1极限和连续性 2.1.1极限 定义(函数的极限):设函数w=f(z)在00,目 δ>0(0<6≤p),使得 0<2-zK8 f(-4 则称A为f(z)当z趋向于z时的极限,记作 lim f(z)=4 z→20 或记作当z→z时,f(2)→A
定义(函数的极限): 设函数 w = f (z) 在 0 0 (0 0, ∃ ⇒ § 2.1 极限和连续性

上游充通大 SHANGHAI JIAO TONG UNIVERSITY 逻辑语言的例子: V国家,ヨ数值,使得:V司机:(司机酒精含量>h)→(司机在该国被判定为醉驾)。 V国家,3两个整数a1,a2,使得:V男人V女人:(男人年龄>a1)∧(女人年龄>a2) 男人和女人在该国可以合法结婚
逻辑语言的例子:

上游充通大学 SHANGHAI JIAO TONG UNIVERSITY §2.1极限和连续性 2.1.1极限 定义(函数的极限):设函数w=f(z)在00,目 δ>0(0<6≤p),使得 0<2-zK8 f(-4 则称A为f(z)当z趋向于z时的极限,记作 lim f(z)=4 z→20 或记作当z→z时,f(2)→A
定义(函数的极限): 设函数 w = f (z) 在 0 0 (0 0, ∃ ⇒ § 2.1 极限和连续性
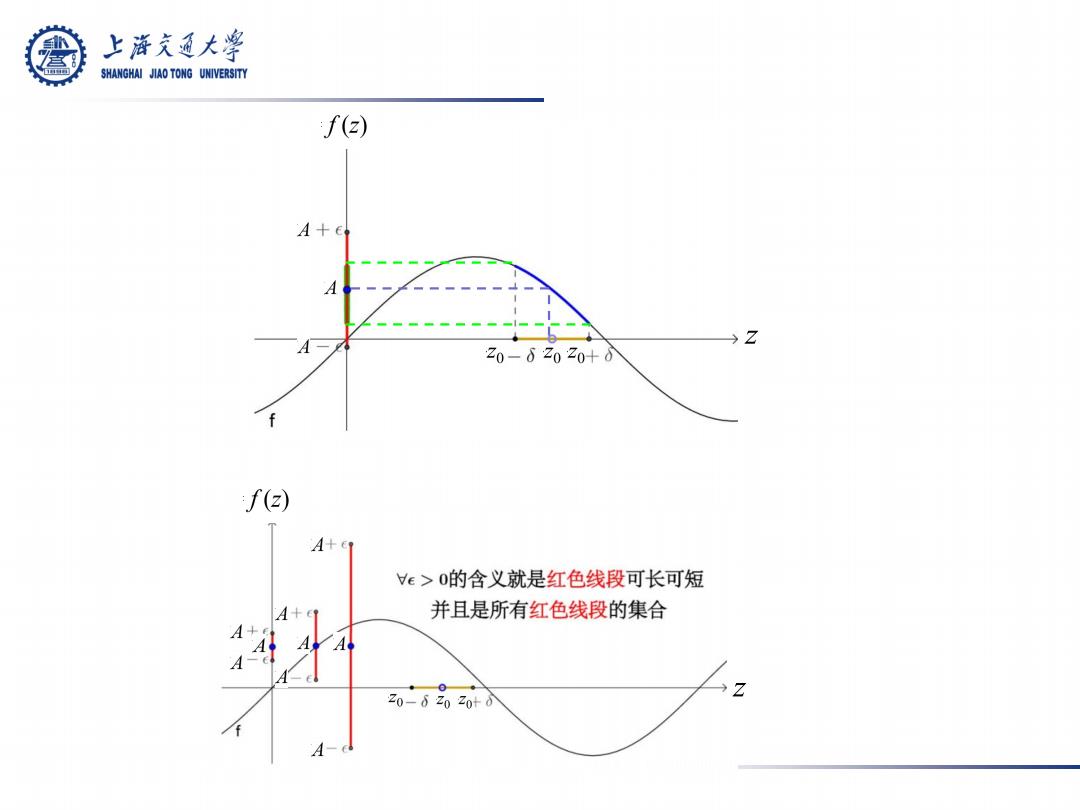
上游充通大学 SHANGHAI JIAO TONG UNIVERSITY /C) A+6 →Z 20-62020+0d A+ e>0的含义就是红色线段可长可短 A+1 并且是所有红色线段的集合 A+ A年A 20-62020+0 A
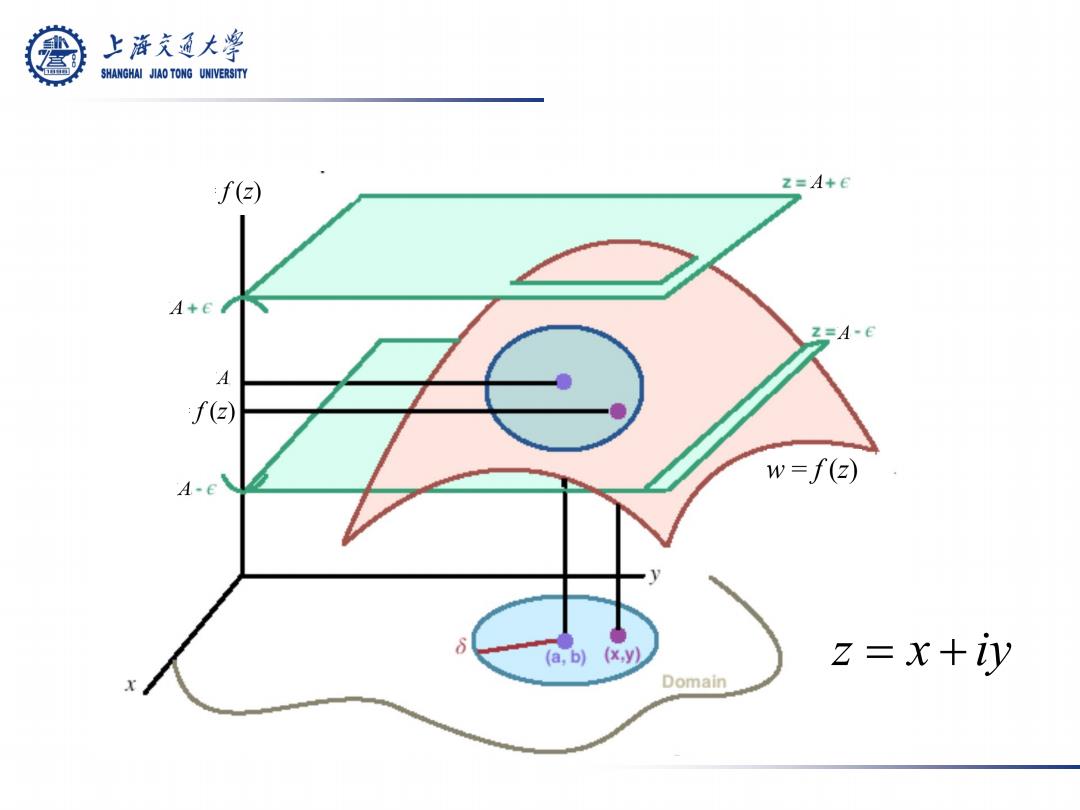
上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY /(C) z=A+E A+E 2=A-E A f(z)) w=f(2) A-e (a,b)(x,y) Z= x iy Domain
z = x + iy

上游充通大 SHANGHAI JIAO TONG UNIVERSITY 复变函数极限的基本定理 设函数f(z)=u(x,y)+iv(x,y), 4=uo+ivo,zo=xo+ivo,limf(z)=A 的充要条件是 lim u(x,y)=uo lim v(x,y)vo x→x0,y>y0 x->x0,y->yo
0 , 0 , 0 0 0 0 0 lim ( , ) lim ( , ) , , lim ( ) ( ) ( , ) ( , ), 0 0 0 0 0 u x y u v x y v A u iv z x iy f z A f z u x y iv x y x x y y x x y y z z = = = + = + = = + → → → → → 的充要条件是 则 设函数 复变函数极限的基本定理