
上浒充通大学 SHANGHAI JIAO TONG UNIVERSITY 数学物理方法 上海交通大学数学科学学院 李松挺 Email:songting@situ.edu.cn 阖 n 课件:唐异垒老师 ftp://public.sjtu.edu.cn/ user:mathtyl pw:public HANG 1日6
数学物理方法 上海交通大学数学科学学院 李松挺 Email: songting@sjtu.edu.cn 课件:唐异垒老师 ftp://public.sjtu.edu.cn/ user:mathtyl pw:public

上游充通大学 SHANGHAI JIAO TONG UNIVERSITY 课程介绍 考核 平时成绩30%,期末成绩70% 教科书 数学物理方法上海交大出版社上海交通大学数学系组编 数学物理方法高等教育出版社梁昆淼编(参考) 数学物理方法 数学物理方法 延O 第南明
课程介绍 考核 平时成绩 30%, 期末成绩70% 教科书 数学物理方法 上海交大出版社 上海交通大学数学系组编 数学物理方法 高等教育出版社 梁昆淼编 (参考)

上游充通大学 SHANGHAI JIAO TONG UNIVERSITY 第二章复数 1.1复数的表示及运算, 1.2复平面上的点集性质. 1.3复函数与复映射. 1.4复球面与无穷远点
第一章 复数 1.1 复数的表示及运算. 1.2 复平面上的点集性质. 1.3 复函数与复映射. 1.4 复球面与无穷远点

上游充通大 SHANGHAI JIAO TONG UNIVERSITY 复数的起源 W→Z→Q→R→C Tartaglia Cardano
复数的起源 N ZQRC →→→→ Tartaglia Cardano

上游充通大 SHANGHAI JIAO TONG UNIVERSITY §1.1复数 1.1.1复数的基本概念 复数的定义(代数式):每个复数具有z=x+y 的形状,其中x和y是实数,是虚数单位(-1的平 方根)。x和y分别称为的实部和虚部,分别记作: x=Rez,y=Imz. 注1:复数相等,即两复数实部与虚部分别相等 注2:两复数不可以比较大小
§ 1.1 复数 复数的定义(代数式):每个复数具有 z=x+iy 的形状,其中x和y是实数,i是虚数单位(-1的平 方根)。x和y分别称为z的实部和虚部,分别记作: x zy z = = Re , Im . 注1:复数相等, 即两复数实部与虚部分别相等. 注2:两复数不可以比较大小. 1.1.1 复数的基本概念

上游充通大兽 特殊复数 SHANGHAI JIAO TONG UNIVERSITY 如果mz=0,则z看成一个实数; 如果Imz不等于零,那么称z为一个虚数; 如果Imz不等于零,而Rez=0,则称z为一个纯虚数。 1.1.2复数的共轭运算与四则运算 2=x+y,2=x-y,x,y∈R (a1+ib,)±(a2+ib2)=(a1±a2)+(b±b2) (a1+ib,(a2+ib2)=(a,a2-b,b2)+i(a,b2+a2b) (a+ib) daz+bb.iabdbz (a2+b2)a+b a2+b2
特殊复数 如果 Imz=0,则z看成一个实数; 如果 Imz不等于零,那么称z为一个虚数; 如果 Imz不等于零,而Rez=0,则称z为一个纯虚数。 ( ) ( ) ( ) ( ) 1 1 2 2 1 2 1 2 a + ib ± a + ib = a ± a + i b ± b 1.1.2 复数的共轭运算与四则运算 ( )( ) ( ) ( ) 1 1 2 2 1 2 1 2 1 2 2 1 a + ib a + ib = a a − b b + i a b + a b 2 2 2 2 2 1 1 2 2 2 2 2 1 2 1 2 2 2 1 1 ( ) ( ) a b a b a b i a b a a b b a ib a ib + − + + + = + + z x iy z x iy x y R =+ =− ∈ ,

上游充通大学 SHANGHAI JIAO TONG UNIVERSITY 复数在四则运算这个代数结构下,构成一个数域 (对加、减、乘、除运算封闭,对加乘具有交换律、结合律 与分配律,加乘具有单位元与逆元),称为复数域, 记为C,复数域可以看成实数域的扩张
复数在四则运算这个代数结构下,构成一个数域 (对加、减、乘、除运算封闭,对加乘具有交换律、结合律 与分配律,加乘具有单位元与逆元),称为复数域, 记为C, 复数域可以看成实数域的扩张

上游充通大 1.1.3 复数的几何意义 SHANGHAI JIAO TONG UNIVERSITY 一个复数z=x+y本质上由一对有序实数对(x,y) 唯一确定。作映射: 1-1对应 C→R2:z=x+iyS(x,y) (双射) 复数域C也可以理解成平面RxR,我们称C为 复平面. 平面上横坐标轴称为实轴,纵坐标轴称为虚 轴. 注:C中“数”与复平面上“点”看作等同
1.1.3 复数的几何意义 复数域C 也可以理解成平面RxR,我们称C为 复平面. 平面上横坐标轴称为实轴,纵坐标轴称为虚 轴. : ( , ) 2 C → R z = x + iy x y 一个复数 z=x+iy 本质上由一对有序实数对(x, y) 唯一确定。作映射: 1-1对应 (双射) 注:C中“数”与复平面上“点”看作等同
上游充通大兽 SHANGHAI JIAO TONG UNIVERSITY 复数的向量表示 (x,y) C上向量与复数z=x+业也构成 一一 对应的关系,则复数可以等同于平面 中的向量等价类(在平移关系下)。向量 的长度称为复数的模,定义为 |z=√x2+y2= Z与正实轴之间的夹角称为复数的辐角,定义为: Argz=0+2kπcR,K为整数. 注1:z=0时辐角无意义。z卡0时Agz为无穷多值函数,辐角 的多值性是很多复变函数多值性的根源. 注2:两个复数相等的充要条件:它们模相等,辐角相差2kπ
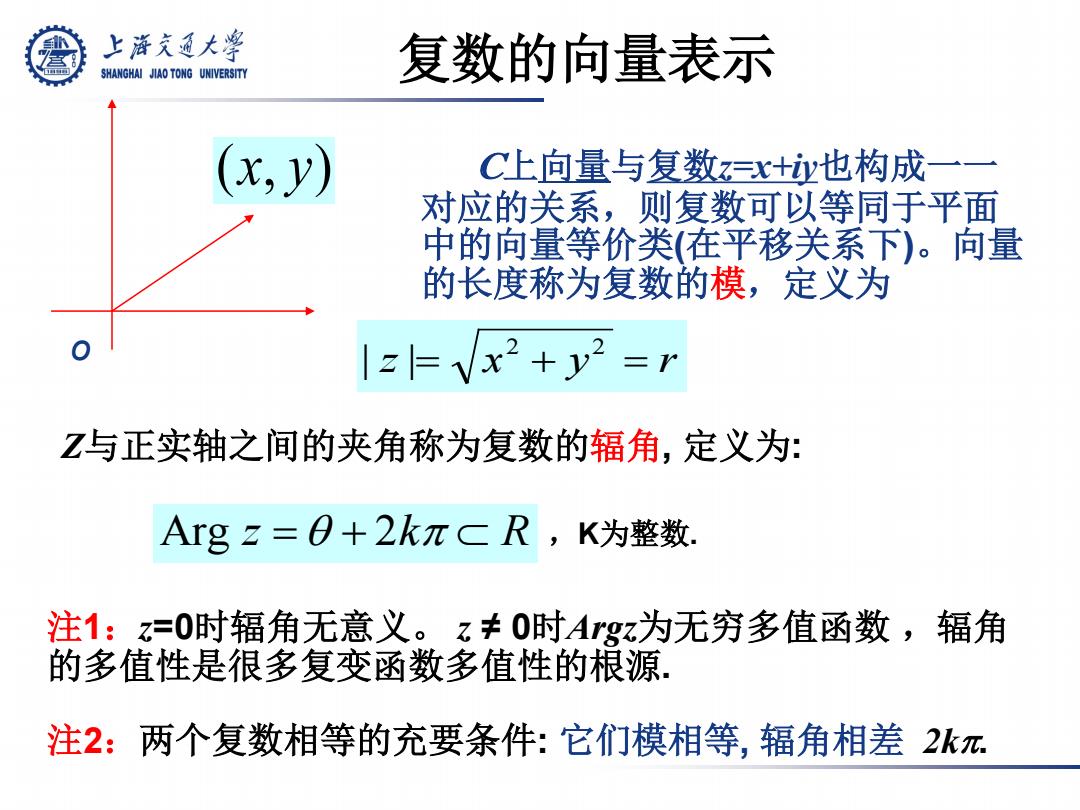
复数的向量表示 C上向量与复数z=x+iy也构成一一 对应的关系,则复数可以等同于平面 中的向量等价类(在平移关系下)。向量 的长度称为复数的模,定义为 z = x + y = r 2 2 | | Z与正实轴之间的夹角称为复数的辐角, 定义为: Arg 2 z kR =+ ⊂ θ π 注1:z=0时辐角无意义。 z ≠ 0时Argz为无穷多值函数 ,辐角 的多值性是很多复变函数多值性的根源. (x, y) ,K为整数. o 注2:两个复数相等的充要条件: 它们模相等, 辐角相差 2kπ

上游充通大粤 SHANGHAI JIAO TONG UNIVERSITY 辐角主值argz:取Argz的一个属于 (一π,π]之间的特殊值. arctan上 x>0, X π 21 x=0,y>0, arg z =arctan +, x<0,y≥0, x arctan y -π, x<0,y<0, X π x=0,y<0 2 Argz=argz+2kπ,k∈Z
辐角主值argz:取Argz的一个属于 ( ] −π ,π 之间的特殊值. − = > = , 0, 0. 2 arctan , 0, 0, arctan , 0, 0, , 0, 0, 2 arctan , 0, arg x y x y x y x y x y x y x x y z π π π π Arg arg 2 , z z kk =+ ∈ π Z