
第1章命题逻辑 第1章命题逻辑 1.1命题及联结词 1.2命题公式与翻译 1.3真值表和等价公式 1.4重言式 1.5范式 1.6全功能联结词集 1.7对偶式与蕴含式 1.8命题逻辑的推理理论 返回总目录
第1章 命题逻辑 第1章 命题逻辑 1.1 命题及联结词 1.2 命题公式与翻译 1.3 真值表和等价公式 1.4 重言式 1.5 范式 1.6 全功能联结词集 1.7 对偶式与蕴含式 1.8 命题逻辑的推理理论 返回总目录

第1章命题逻辑 第1章命题逻辑 1.1命题及联结词 1.1.1命题的基本概念 在数理逻辑中把能判断真假的陈述句称为命题。一般 用小写英文字母或小写英文字母带下标表示。 命题的概念包含了以下3个要素: (1)只有陈述句才有可能成为命题,而其它的语句,如: 感叹句、祈使句、疑问句等都不是命题 (2)一个语句虽是陈述句,但不能判断真假不是命题。 (3)虽然要求命题能判断真假,但不要求现在就能确定 真假,将来可以确定真假也可以。 一个命题表达的判断结果称为命题的真值。命题的真 值有“真”和“假”两种,分别用True、T、1(真)和False、 F、0(假)来表示。真值为真的命题称为真命题,真值为假 的命题称为假命题。任何命题的真值是惟一的
第1章 命题逻辑 第1章 命题逻辑 1.1命题及联结词 1.1.1 命题的基本概念 在数理逻辑中把能判断真假的陈述句称为命题。一般 用小写英文字母或小写英文字母带下标表示。 命题的概念包含了以下3个要素: ⑴只有陈述句才有可能成为命题,而其它的语句,如: 感叹句、祈使句、疑问句等都不是命题。 ⑵一个语句虽是陈述句,但不能判断真假不是命题。 ⑶虽然要求命题能判断真假,但不要求现在就能确定 真假,将来可以确定真假也可以。 一个命题表达的判断结果称为命题的真值。命题的真 值有“真”和“假”两种,分别用True、T、1(真)和False、 F、0(假)来表示。真值为真的命题称为真命题,真值为假 的命题称为假命题。任何命题的真值是惟一的

第1章命题逻精 在命题逻辑中对命题不再细分,因而命题是数理逻辑中 最基本的也是最小的研究单位 。 【例11】判断以下语句是否为命题。若是命题,确定 其真值。 (1)上海是个小村庄。 (2)存在外星人。 (3)禁止吸烟! (4)北京是中国的首都。 (⑤)4是素数或6是素数。 (6)今天你吃了吗? (7)11+1=100 (8)我正在说谎。 解:(1)命题(),(2)命题(待定),(3)不是命题(祈使句) (4)命题(T),(⑤)命题(F),(6)不是命题(疑问句),(7)命题(由 上下文确定),(8)不是命题(悖论)
第1章 命题逻辑 在命题逻辑中对命题不再细分,因而命题是数理逻辑中 最基本的也是最小的研究单位。 【例1.1】判断以下语句是否为命题。若是命题,确定 其真值。 ⑴上海是个小村庄。 ⑵存在外星人。 ⑶禁止吸烟! ⑷北京是中国的首都。 ⑸4是素数或6是素数。 ⑹今天你吃了吗? ⑺11+1=100 ⑻我正在说谎。 解:⑴命题(F),⑵命题(待定),⑶不是命题(祈使句), ⑷命题(T),⑸命题(F),⑹不是命题(疑问句), ⑺命题(由 上下文确定),⑻ 不是命题(悖论)

第1章命题逻辑 表示命题的小写英文字母或带下标的小写英文字母常称 为命题标识符。如果命题标识符表示一个具体、确定的命题, 称为命题常元。如果命题标识符表示任意一个命题,称为命 题变元。命题变元无确定的真值。 命题是能判断真假的陈述句。而命题变元代表任意的命 题,其真值是不确定的。因而不是命题。 如果一个命题不能再分解成更简单的命题,则称该命题 为原子命题。如果一个命题不是原子命题,称该命题为复合 命题。 如果命题变元表示原子命题时,该命题变元称为原子变 元。 在自然语言中,可以通过“如果…,那么…” ,”不 但…,而且…”这样的连词将简单的陈述句联结成复合语句 同样在命题逻辑当中,也可以通过命题联结词将原子变元联 结起来表示复合命题
第1章 命题逻辑 表示命题的小写英文字母或带下标的小写英文字母常称 为命题标识符。如果命题标识符表示一个具体、确定的命题, 称为命题常元。如果命题标识符表示任意一个命题,称为命 题变元。命题变元无确定的真值。 命题是能判断真假的陈述句。而命题变元代表任意的命 题,其真值是不确定的。因而不是命题。 如果一个命题不能再分解成更简单的命题,则称该命题 为原子命题。如果一个命题不是原子命题,称该命题为复合 命题。 如果命题变元表示原子命题时,该命题变元称为原子变 元。 在自然语言中,可以通过“如果…,那么…” , “不 但…,而且…”这样的连词将简单的陈述句联结成复合语句, 同样在命题逻辑当中,也可以通过命题联结词将原子变元联 结起来表示复合命题

第1章命题逻辑 1.1.2命题联结词 常用的逻辑联结词有五种:否定联结 词、合取联结词、析取联结词、条件联结 表1.1 词和双条件联结词。 1.否定联结词 p Tp 定义1.1.1设p为命题,则p的否定是一 0 1 个复合命题,记作:p,读作“非p”或 “p的否定”。定义为:若P为T,则p为F; 1 0 若p为F,则p的真值为T。 p和一p的关系如表1.1所示,表1.1叫做否定联结词“” 的真值表(下同)。 联结词””也可以看作逻辑运算,它是一元运算。 【例1.2】否定下列命题。 p:王强是一名大学生。 p:王强不是一名大学生
第1章 命题逻辑 1.1.2 命题联结词 常用的逻辑联结词有五种:否定联结 词、合取联结词、析取联结词、条件联结 词和双条件联结词。 1. 否定联结词 定义1.1.1 设p为命题,则p的否定是一 个复合命题,记作:¬p,读作“非p ”或 “ p的否定” 。定义为:若P为T,则¬p为F; 若p为F,则¬p的真值为T。 表1.1 p ¬p 0 1 1 0 p和¬p的关系如表1.1所示,表1.1叫做否定联结词“¬” 的真值表(下同)。 联结词“ ¬ ”也可以看作逻辑运算,它是一元运算。 【例1.2】否定下列命题。 p:王强是一名大学生。 ¬p:王强不是一名大学生
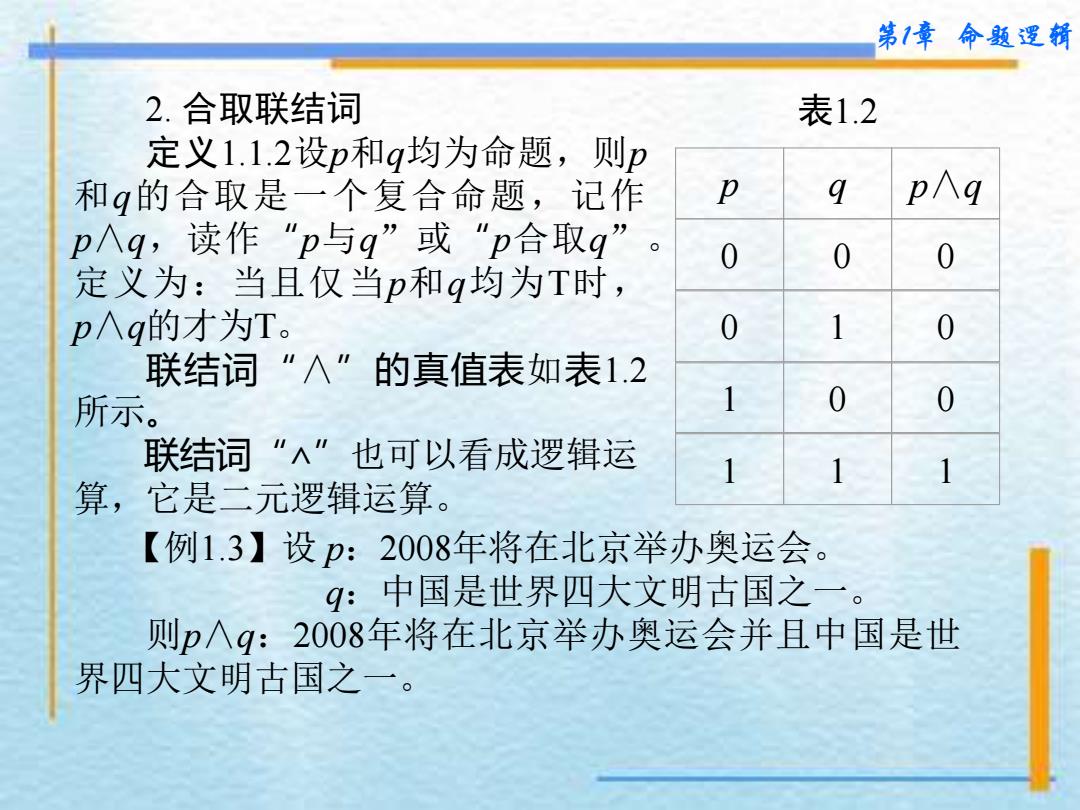
第1章命题逻精 2.合取联结词 表1.2 定义1.1.2设p和g均为命题,则p 和g的合取是一个复合命题,记作 p 9 p∧q p∧q,读作"p与g”或“p合取q 0 0 0 定义为:当且仅当p和g均为T时 p∧g的才为T。 0 1 0 联结词“个”的真值表如表1.2 所示。 1 0 0 联结词“∧”也可以看成逻辑运 1 1 1 算,它是二元逻辑运算。 【例1.3】设p:2008年将在北京举办奥运会。 9:中国是世界四大文明古国之一。 则p个g:2008年将在北京举办奥运会并且中国是世 界四大文明古国之一
第1章 命题逻辑 2. 合取联结词 定义1.1.2设p和q均为命题,则p 和q的合取是一个复合命题,记作 p∧q,读作“ p与q ”或“ p合取q ” 。 定义为:当且仅当p和q均为T时, p∧q的才为T。 联结词“∧”的真值表如表1.2 所示。 联结词“∧”也可以看成逻辑运 算,它是二元逻辑运算。 表1.2 p q p∧q 0 0 0 0 1 0 1 0 0 1 1 1 【例1.3】设 p:2008年将在北京举办奥运会。 q:中国是世界四大文明古国之一。 则p∧q:2008年将在北京举办奥运会并且中国是世 界四大文明古国之一
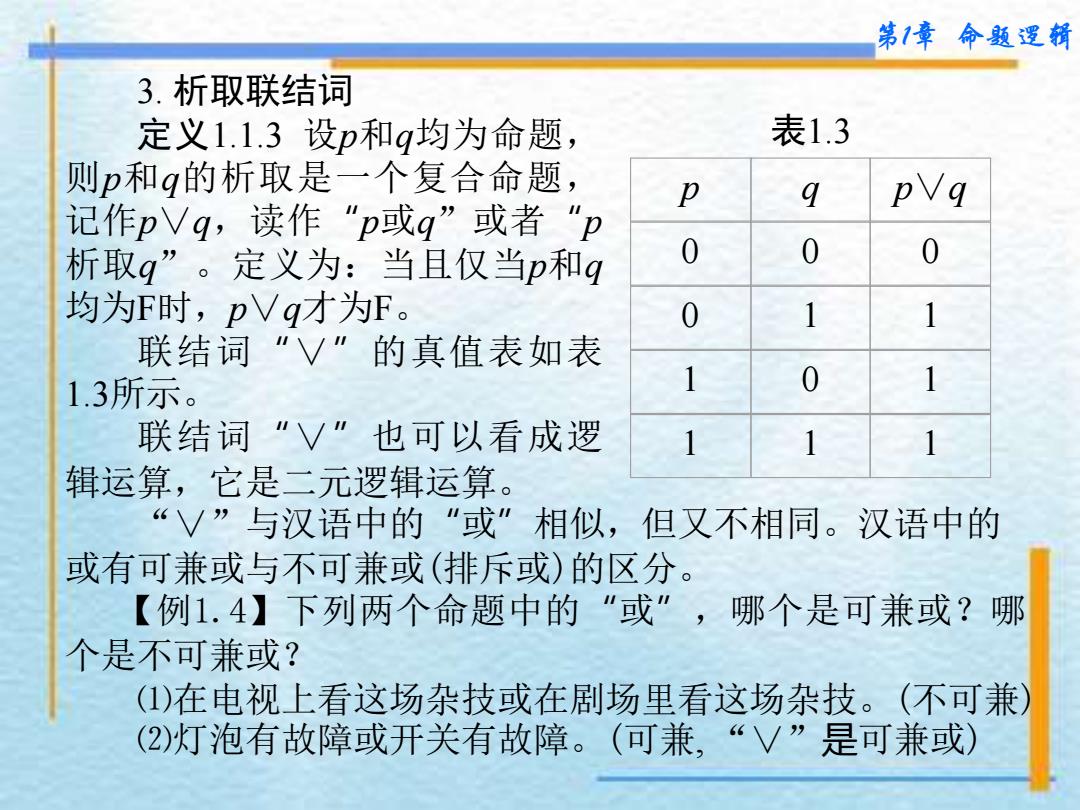
第1章命题逻辑 3.析取联结词 定义1.1.3设p和q均为命题 表1.3 则p和g的析取是一个复合命题 p q pVq 记作pVq,读作"p或q”或者"p 析取g”。定义为:当且仅当p和q 0 0 0 均为F时,pVq才为F。 0 1 1 联结词”V”的真值表如表 1.3所示。 1 0 1 联结词“V”也可以看成逻 1 1 1 辑运算,它是二元逻辑运算。 “V”与汉语中的“或”相似,但又不相同。汉语中的 或有可兼或与不可兼或(排斥或)的区分。 【例1.4】下列两个命题中的“或”,哪个是可兼或?哪 个是不可兼或? (1)在电视上看这场杂技或在剧场里看这场杂技。(不可兼) (2)灯泡有故障或开关有故障。(可兼,“V”是可兼或)
第1章 命题逻辑 3. 析取联结词 定义1.1.3 设p和q均为命题, 则p和q的析取是一个复合命题, 记作p∨q,读作“ p或q ”或者“ p 析取q ” 。定义为:当且仅当p和q 均为F时,p∨q才为F。 联结词“∨”的真值表如表 1.3所示。 联结词“∨”也可以看成逻 辑运算,它是二元逻辑运算。 表1.3 p q p∨q 0 0 0 0 1 1 1 0 1 1 1 1 “∨”与汉语中的“或”相似,但又不相同。汉语中的 或有可兼或与不可兼或(排斥或)的区分。 【例1.4】下列两个命题中的“或” ,哪个是可兼或?哪 个是不可兼或? ⑴在电视上看这场杂技或在剧场里看这场杂技。(不可兼) ⑵灯泡有故障或开关有故障。(可兼, “∨”是可兼或)
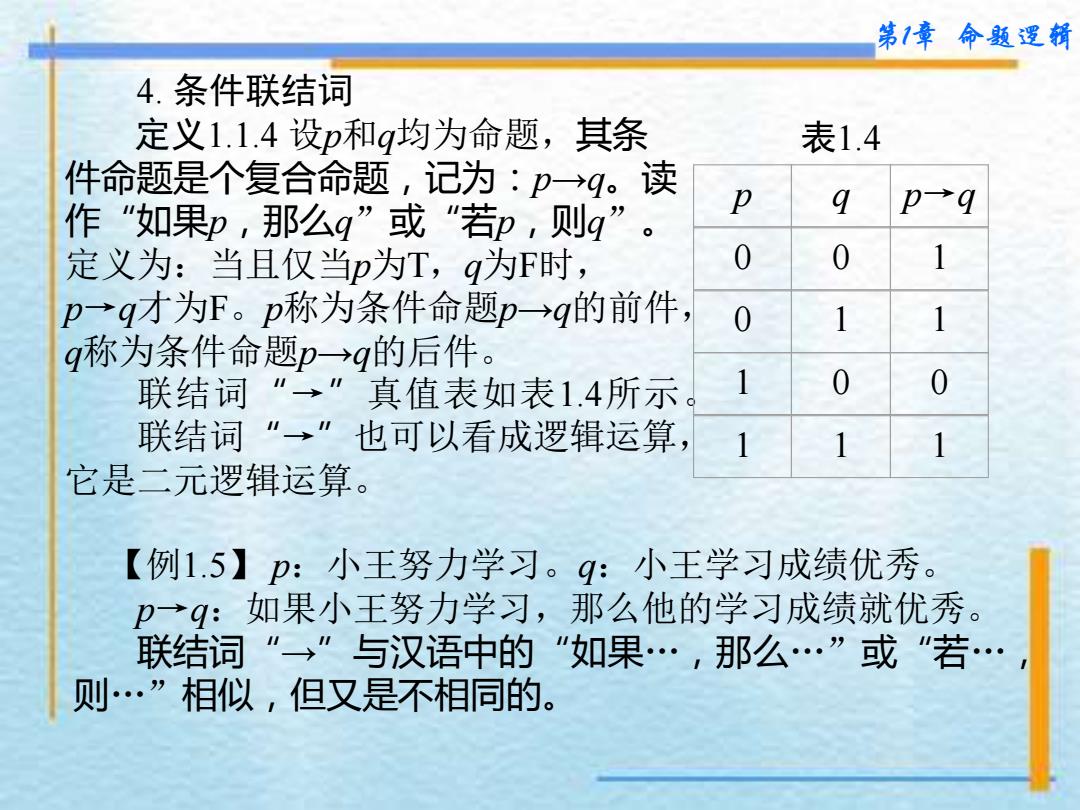
第1章命题逻辑 4.条件联结词 定义1.1.4设p和g均为命题,其条 表1.4 件命题是个复合命题,记为:p→q。读 作”如果p,那么g”或"若,则g”。 q p→q 定义为:当且仅当p为T,q为F时, 0 0 1 p→q才为F。p称为条件命题p→q的前件 0 1 1 q称为条件命题p→9的后件。 联结词 真值表如表1.4所示 1 0 0 联结词”→” 也可以看成逻辑运算, 1 1 1 它是二元逻辑运算。 【例1.5】p:小王努力学习。q:小王学习成绩优秀。 p→9:如果小王努力学习,那么他的学习成绩就优秀。 联结词”→”与汉语中的“如果…,那么…”或“若 则…”相似,但又是不相同的
第1章 命题逻辑 4. 条件联结词 定义1.1.4 设p和q均为命题,其条 件命题是个复合命题,记为:p→q。读 作“如果p,那么q ”或“若p,则q ” 。 定义为:当且仅当p为T,q为F时, p→q才为F。p称为条件命题p→q的前件, q称为条件命题p→q的后件。 联结词“ → ”真值表如表1.4所示。 联结词“ → ”也可以看成逻辑运算, 它是二元逻辑运算。 表1.4 p q p→q 0 0 1 0 1 1 1 0 0 1 1 1 【例1.5】 p:小王努力学习。q:小王学习成绩优秀。 p→q:如果小王努力学习,那么他的学习成绩就优秀。 联结词“ → ”与汉语中的“如果…,那么…”或“若…, 则…”相似,但又是不相同的
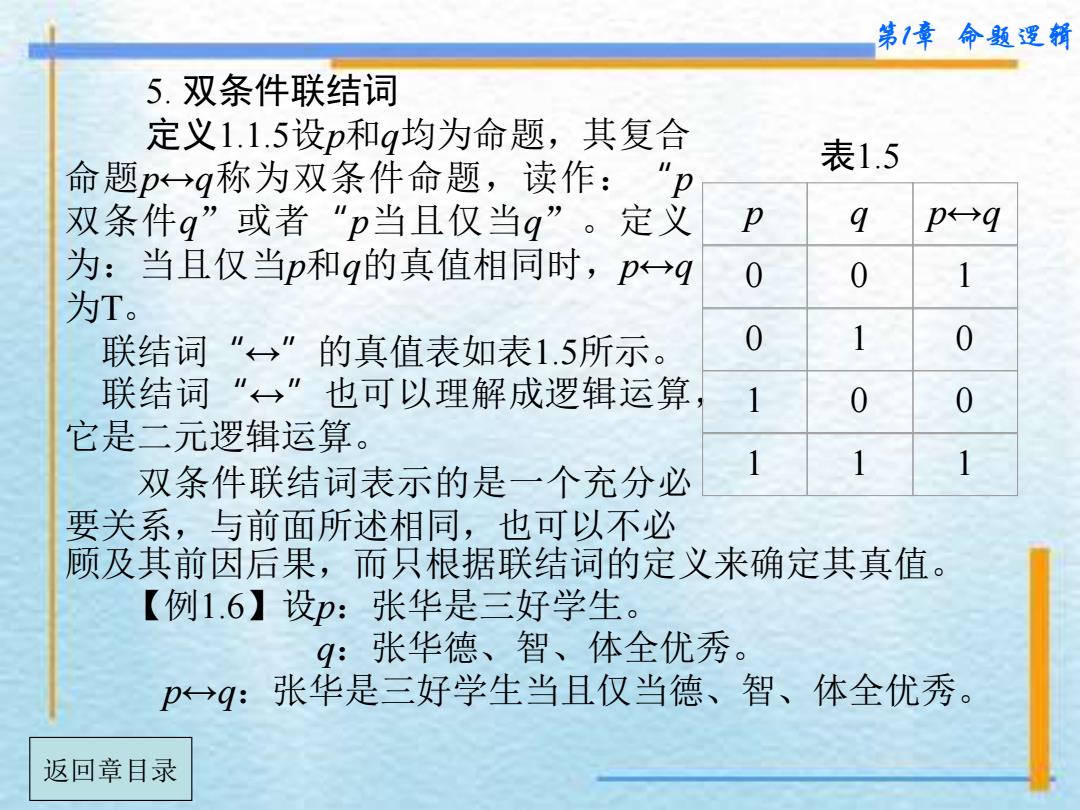
第1章命数逻辑 5.双条件联结词 定义1.1.5设p和g均为命题,其复合 命题p>q称为双条件命题,读作:”p 表1.5 双条件g”或者“p当且仅当g”。定义 卫 9 p→9 为:当且仅当p和q的真值相同时,p→q 0 0 1 为T。 联结词“←→” 的真值表如表1.5所示。 0 1 0 联结词“←→”也可以理解成逻辑运算 1 0 0 它是二元逻辑运算。 双条件联结词表示的是一个充分必 1 1 1 要关系,与前面所述相同,也可以不必 顾及其前因后果,而只根据联结词的定义来确定其真值。 【例1.6】设p:张华是三好学生。 9:张华德、智、体全优秀。 pq:张华是三好学生当且仅当德、智、体全优秀。 返回章目录
第1章 命题逻辑 5. 双条件联结词 定义1.1.5设p和q均为命题,其复合 命题p↔q称为双条件命题,读作:“ p 双条件q ”或者“ p当且仅当q ” 。定义 为:当且仅当p和q的真值相同时,p↔q 为T。 联结词“ ↔ ”的真值表如表1.5所示。 联结词“ ↔ ”也可以理解成逻辑运算, 它是二元逻辑运算。 双条件联结词表示的是一个充分必 要关系,与前面所述相同,也可以不必 表1.5 p q p↔q 0 0 1 0 1 0 1 0 0 1 1 1 顾及其前因后果,而只根据联结词的定义来确定其真值。 【例1.6】设p:张华是三好学生。 q:张华德、智、体全优秀。 p↔q:张华是三好学生当且仅当德、智、体全优秀。 返回章目录

第1章命题逻新 1.2命题公式与翻译 把命题常量,命题变量按照一定的逻辑顺序用命题联结 词连接起来就构成了命题演算的合式公式,也叫命题公式。 当使用联结词集,∧,V,,→时,合式公式定义如下: 定义1.2.1按下列规则构成的符号串称为命题演算的合式 公式,也称为命题公式,简称公式。 (1)单个命题变元和常元是合式公式。 (2)如果A是合式公式,那么A是合式公式。 (3)如果A和B是合式公式,那么(A∧B)、(AVB)、(A→B) 和(A→B)是合式公式。 (4)当且仅当有限次地应用了(1)、(2)、(3)所得到的符号串 是合式公式。 命题公式一般的用大写的英文字母A,B,C,…表示。 依照这个定义,下列符号串是合式公式:
第1章 命题逻辑 1.2 命题公式与翻译 把命题常量,命题变量按照一定的逻辑顺序用命题联结 词连接起来就构成了命题演算的合式公式,也叫命题公式。 当使用联结词集¬,∧,∨,→,↔时,合式公式定义如下: 定义1.2.1按下列规则构成的符号串称为命题演算的合式 公式,也称为命题公式,简称公式。 ⑴单个命题变元和常元是合式公式。 ⑵如果A是合式公式,那么¬A是合式公式。 ⑶如果A和B是合式公式,那么(A∧B)、(A∨B)、(A→B) 和(A↔B)是合式公式。 ⑷当且仅当有限次地应用了⑴、⑵、⑶所得到的符号串 是合式公式。 命题公式一般的用大写的英文字母A,B,C,…表示。 依照这个定义,下列符号串是合式公式: