
第6章 共形映射 By 付小宁
1 第6章 共形映射 By 付小宁

§1共形映射的概念 z平面内的任一条有向曲线C可用=z(),≤长B 表示,它的正向取为增大时点z移动的方向,()为一 条连续函数 如果z'(o)≠0,心<邛,则表示z'()的向量(把起点 放取在z0.以下不一一说明)与C相切于点20z(o) z'( z(to) z(0
2 z 平面内的任一条有向曲线C可用 z=z(t), atb 表示, 它的正向取为t增大时点z移动的方向, z(t)为一 条连续函数. 如果z '(t0 )0,a<t0<b, 则表示z '(t)的向量(把起点 放取在z0 . 以下不一一说明)与C相切于点z0 =z(t0 ). z(t0 ) z(a) z(b) z '(t0 ) §1 共形映射的概念
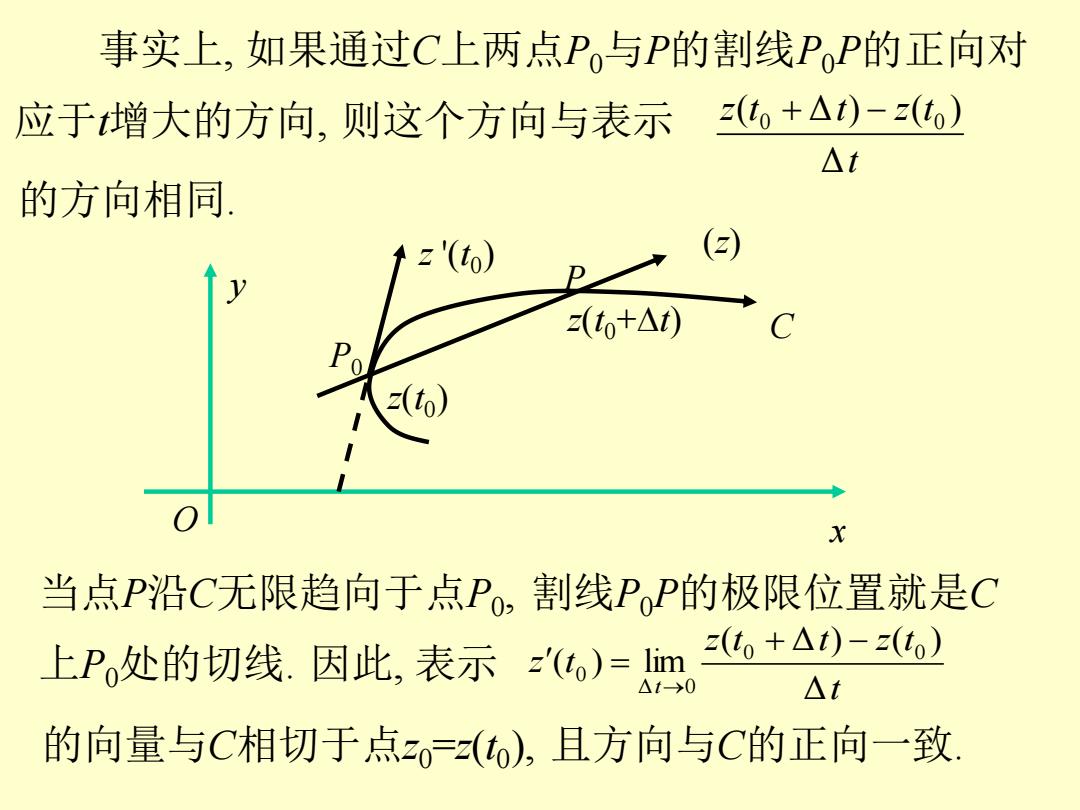
事实上,如果通过C上两点P与P的割线PP的正向对 应于增大的方向,则这个方向与表示 z(t+△t)-z(to) △t 的方向相同, 12'() () z(t,+△t) 2(o) x 当点P沿C无限趋向于点P,割线PP的极限位置就是C 上Po处的切线.因此,表示(o)=m z(t。+△t)-z(to) t-→0 △t 的向量与C相切于点z0=z(0),且方向与C的正向一致
3 事实上, 如果通过C上两点P0与P的割线P0P的正向对 应于t增大的方向, 则这个方向与表示 t z t t z t Δ ( Δ ) ( ) 0 + − 0 的方向相同. O x y z(t0 ) P0 P z(t0+Dt) C (z) 当点P沿C无限趋向于点P0 , 割线P0P的极限位置就是C 上P0处的切线. 因此, 表示 t z t t z t z t t Δ ( Δ ) ( ) ( ) lim 0 0 Δ 0 0 + − = → 的向量与C相切于点z0=z(t0 ), 且方向与C的正向一致. z '(t0 )

我们有 1)Argz'(to)就是zo处C的切线正向与x轴正向间的夹角; 2) 相交于一点的两条曲线C,与C2正向之间的夹角就是它 们交点处切线正向间夹角 (2) ◆ O X
4 我们有 1) Arg z '(t0 )就是z0处C的切线正向与x轴正向间的夹角; 2) 相交于一点的两条曲线C1与C2正向之间的夹角就是它 们交点处切线正向间夹角 O x (z) z0 C1 C2

设函数w=孔z)将点z,z+△z分别影射为w, w+△w,向量(z,z+△z)与实轴的夹角为0、 向量(w,w+△w)与实轴的夹角为p,则称 p-0为影射w=z)产生的角度转动,即 中-B=Ar8[f(z+△2)-f(z]-Ag[(z+△)-2] Arg f(=+A)-f()=Arg f(z+△)-f(z) (z+△2)-2 △正 f(z+△)-f(2) 点z处转动角 m(0-)=,4g △2→0 △z 当w=z)解析时,点z处转动角=Ag'(z)
5 设函数w=f(z)将点z,z+∆z分别影射为w, w+∆w,向量(z,z+∆z)与实轴的夹角为θ、 向量(w,w+∆w)与实轴的夹角为φ,则称 φ- θ 为影射w=f(z) 产生的角度转动,即 点z处转动角 当w=f(z)解析时,点z处转动角= z f z z f z Arg z z z f z z f z Arg Arg f z z f z Arg z z z D + D − = + D − + D − = − = + D − − + D − ( ) ( ) ( ) ( ) ( ) [ ( ) ( ) ] [ ( ) ] Argf (z) z f z z f z Arg z z D + D − − = D → D → ( ) ( ) lim ( ) lim 0 0

类似地,可定义函数w=孔z)在z处的伸 缩率 lim Lf(+A)-f()l=lim f(+A)-f(=) △z→0 |(2+△2)-z Λ0 当w=z)解析时,点z处伸缩率f'(z)川 Note:若f(z)=Z,f'(z)不存在,而伸缩率 lim 1z+A- lim 0|z+△z-z|0|△z
6 类似地,可定义函数w=f(z)在z处的伸 缩率 当w=f(z)解析时,点z处伸缩率 Note: 若 不存在,而伸缩率 | ( ) ( ) lim | | ( ) | | ( ) ( )| lim 0 0 z f z z f z z z z f z z f z z z D + D − = + D − + D − D → D → =| f (z)| 1 | | | | lim | | | | lim 0 0 D D = + D − + D − D → D → z z z z z z z z z z f (z) = Z, f (z)

1.解析函数的导数的几何意义设函数w=f()在区域D内 解析,为D内的一点,且f'(zo)≠0.又设C为z平面内通过点 zo的一条有向光滑曲线:2=z(t),0≤乃,且z0=z(to),z'(to)≠0, toco () gf(,)=@-)=8-8 (a) (w) u
7 1.解析函数的导数的几何意义 设函数w=f (z)在区域D内 解析, z0为D内的一点, 且f '(z0 )0. 又设C为z平面内通过点 z0的一条有向光滑曲线: z=z(t), atb,且z0=z(t0 ), z '(t0 )0, a<t0<b. 映射w=f (z)将C映射成w平面内通过点z0的对应点 w0=f (z0 )的一条有向光滑曲线G : w=f [z(t)], atb . ( ) 0 0 ( ) 0 0 0 0 e lim lim lim lim e e i i i z z z x z w w w w w f z z z z z z − → D → D→ D → − D D D = = = = − D D D O x y O u v z0 P0 r z Dz P C (z) (w) G w0 Q0 Q w r Dw 0 0 ( 0 0 0 0 ) ( ) ( ) 0 0 lim , lim z z w f z Arg f z z D → D → D = = − = − D

w 20 u 根据复合函数求导法,有w'(t)=∫'o)z'(to)≠0. 因此,在上点w处也有切线存在,且切线正向与轴正向 的夹角是Argw'(t)=Argf'(zo)+Agz'(to) Argf"(zo)=Arg w'(to)-Arg='(to)=o-0. 若原来的切线的正向与映射过后的切线的正向之间的夹 角理解为曲线C经过w=f(z)映射后在z处的转动角,则 1)导数f'(zo)≠0的辐角Argf'(zo)是曲线C经过w=f(z)映射 后在zo处的转动角;
8 根据复合函数求导法, 有w '(t0 )=f '(z0 )z '(t0 )0. 因此, 在G上点w0处也有切线存在, 且切线正向与u轴正向 的夹角是Arg w '(t0 )=Arg f '(z0 )+Arg z '(t0 ). 若原来的切线的正向与映射过后的切线的正向之间的夹 角理解为曲线C经过w=f (z)映射后在z0处的转动角, 则 1)导数f '(z0 )0的辐角Arg f '(z0 )是曲线C经过w=f (z)映射 后在z0处的转动角; O x y O u v z0 P0 r z Dz P C (z) (w) G w0 Q0 Q w r Dw 0 0 0 0 即Arg f '(z = − . 0 )= Arg w '(t0 )−Arg z '(t0 )
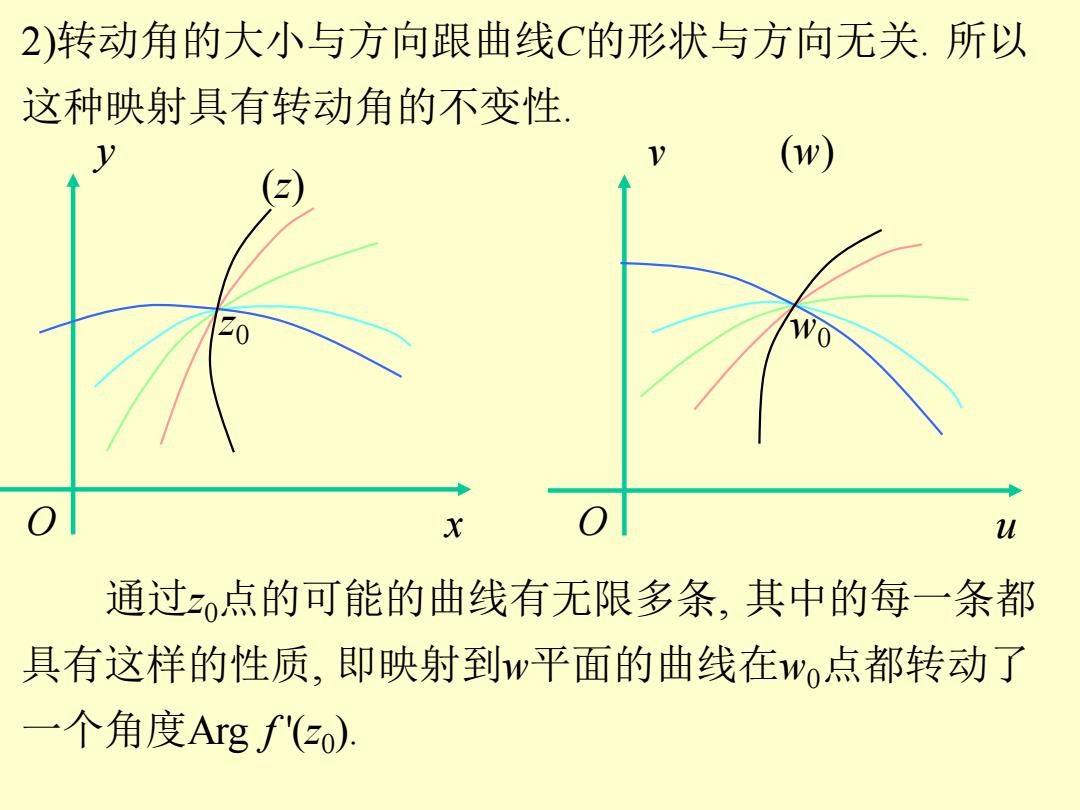
2)转动角的大小与方向跟曲线C的形状与方向无关.所以 这种映射具有转动角的不变性 (w) X u 通过z点的可能的曲线有无限多条,其中的每一条都 具有这样的性质,即映射到w平面的曲线在wo点都转动了 一个角度Argf'(zo)
9 2)转动角的大小与方向跟曲线C的形状与方向无关. 所以 这种映射具有转动角的不变性. 通过z0点的可能的曲线有无限多条, 其中的每一条都 具有这样的性质, 即映射到w平面的曲线在w0点都转动了 一个角度Arg f '(z0 ). O x y O u v (z) (w) z0 w0
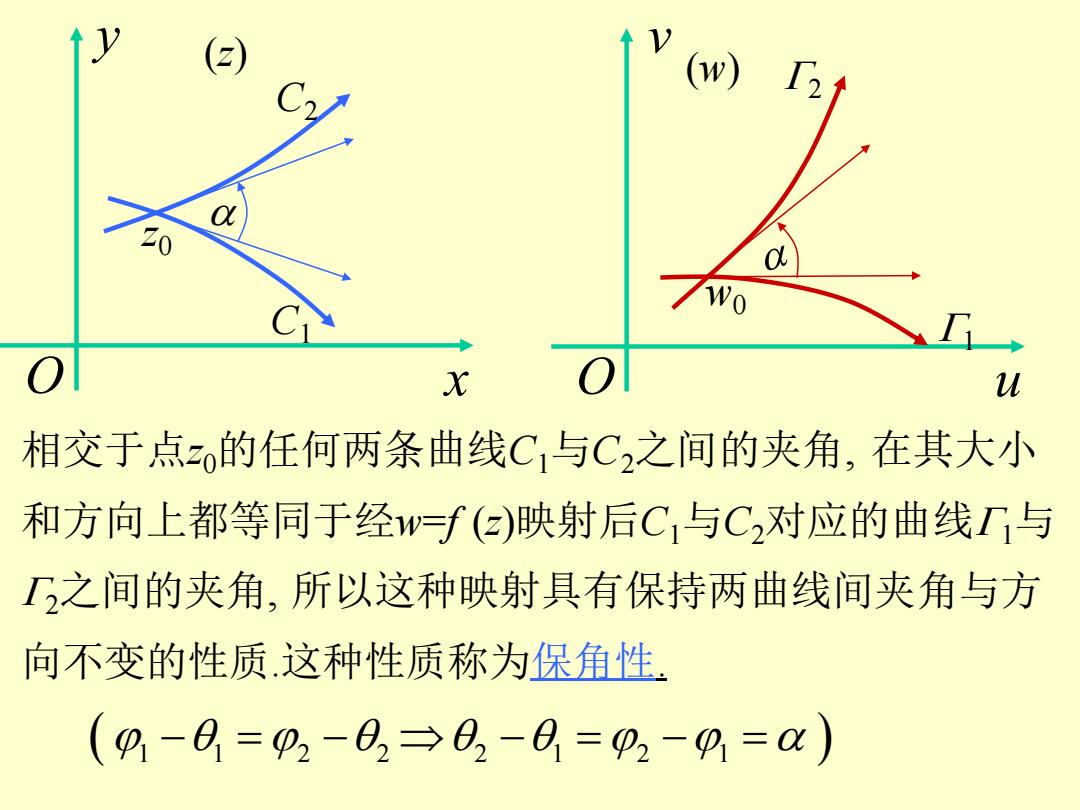
↑y () 7W0 X u 相交于点z0的任何两条曲线C,与C2之间的夹角,在其大小 和方向上都等同于经w=f()映射后C与C2对应的曲线T与 之间的夹角,所以这种映射具有保持两曲线间夹角与方 向不变的性质.这种性质称为保角性 (9-8=p2-82→82-8=p2-0=a)
10 相交于点z0的任何两条曲线C1与C2之间的夹角, 在其大小 和方向上都等同于经w=f (z)映射后C1与C2对应的曲线G1与 G2之间的夹角, 所以这种映射具有保持两曲线间夹角与方 向不变的性质.这种性质称为保角性. y a O x O u v (z) (w) z0 w0 C1 C2 G1 G2 ( a 1 1 2 2 2 1 2 1 − = − − = − = )