
第十三讲Penrose广义逆矩阵(I)
第十三讲 Penrose 广义逆矩阵(I) 1

一、Penrose广义逆矩阵的定义及存在性 所谓广义,即推广了原有概念或结果。我们知道,逆矩阵概念是 针对非奇异的(或称为满秩的)方阵。故这一概念可推广到:(1)奇 异方阵;(2)非方矩阵。事实上,Penrose广义逆矩阵涵盖了两种情况。 对于满秩方阵A,A存在,且AA1=AA=I故,当然有 AAA=A AAA=A (AA)=44 (44)=44 这四个对满秩方阵显然成立的等式构成了Penrose广义逆的启示。 2
一、Penrose 广义逆矩阵的定义及存在性 所谓广义,即推广了原有概念或结果。我们知道,逆矩阵概念是 针对非奇异的(或称为满秩的)方阵。故这一概念可推广到:(1)奇 异方阵;(2)非方矩阵。事实上, Penrose 广义逆矩阵涵盖了两种情况。 对于满秩方阵 A, A−1 存在,且 AA−1 =A−1 A=I 故,当然有 -1 -1 -1 -1 -1 -1 -1 () () H H AA A A A AA A AA AA AA AA = = = = 这四个对满秩方阵显然成立的等式构成了 Penrose 广义逆的启示。 2

1.Penrose定义:设A∈Cmx",若Z∈Cmxm且使如下四个等式成立, AZA=A,ZAZ=Z,(AZ)=AZ,(ZA)=ZA 则称Z为A的Moore-Penrose(广义)逆,记为,A。 而上述四个等式又依次称为Penrose方程(i),(i),(ii,(iv)。 2.Moore-Penrose逆的存在性和唯一性 定理:任给A∈Cmx”,AT均存在且唯一。 证明:存在性.廿A∈C,”,均存在西矩阵U∈Cmm,V∈C”使 3
1. Penrose 定义:设 A∈C m n× ,若 Z∈Cn m× 且使如下四个等式成立, AZA = A, ZAZ = Z, (AZ) H = AZ , (ZA) H = ZA 则称 Z 为 A 的 Moore-Penrose(广义)逆,记为,A† 。 而上述四个等式又依次称为 Penrose 方程(i),(ii) ,(iii) ,(iv)。 2. Moore-Penrose 逆的存在性和唯一性 定理:任给 A∈C m n× ,A† 均存在且唯一。 证明:存在性. ∀ A∈C m n r × ,均存在酉矩阵 U∈C m m m × ,V∈Cn n n × 使 3

62 : 0 UHAV=D = 即A=UDVH Or 0 0 mxn 其中,O,o,,o?是A“A的全部非零特征值。 此时,令Z=VDUH∈Cm 则 4
U H AV = D = 1 2 0 0 0 r m n σ σ σ × 即 A = UDV H 其中, 22 2 1 2 , ,, σσ σ r 是 A H A 的全部非零特征值。 此时,令 Z=V ~ DUH ∈Cn m r × 则 4
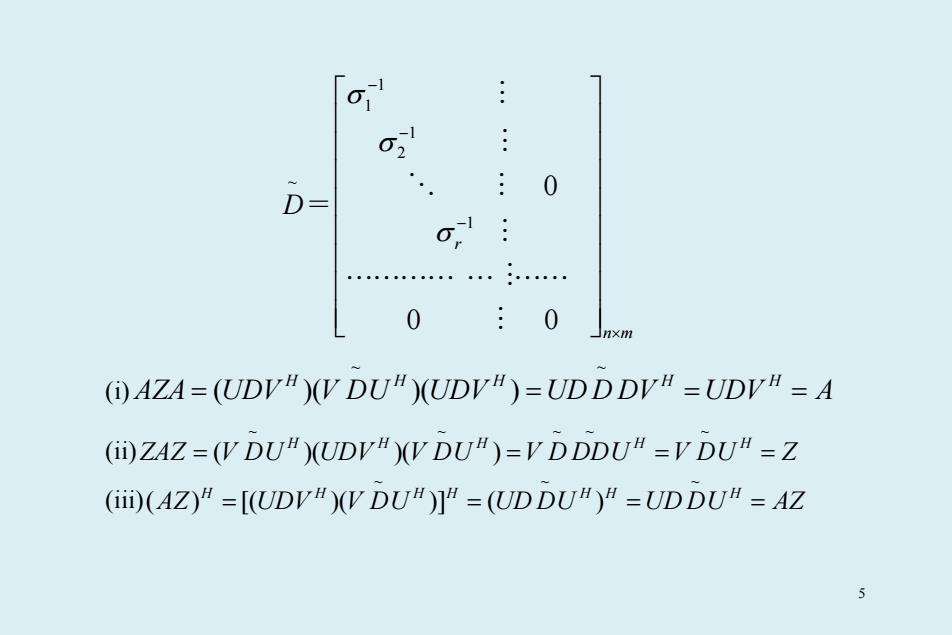
0 D ☐nxm (i)AZA=(UDVH)(V DUR)(UDVA)=UDDDVH =UDVH=A (ii)ZAZ=(V DUH)(UDVH)(V DUH)=V DDDU#=V DU=Z (iii)(AZ)H=[(UDV)(V DUR)]H=(UD DUR)H=UD DUH=AZ 5
~ D= 1 1 1 2 1 0 0 0 r n m σ σ σ − − − × (i) ~ ~ ( )( )( ) H HH H H AZA UDV V DU UDV UD D DV UDV A = = = = (ii) ~ ~ ~ ~ ~ ( )( )( ) HH H H H ZAZ V DU UDV V DU V D DDU V DU Z = = = = (iii) ~ ~~ ( ) [( )( )] ( ) H H H H H H H AZ UDV V DU UD DU UD DU AZ = = = = 5

(iv)(ZA)=(VDDVH)H=V DDVH=ZA 即,Z=A t中o0-[68.00-68 AZ=UDDU, mxm ZA=V DDVH 唯一性:设Z,Y均满足四个Penrose方程,则 6
(iv) ~ ~ () ( ) H H H H ZA V D DV V D DV ZA = = = 即, † Z A = 其 中 ~ 0 0 0 r m m I D D × = ~ 0 0 0 r n n I D D × = ~ H AZ UD DU = , ~ H ZA V D DV = 唯一性:设 Z ,Y 均满足四个 Penrose 方程,则 6

Z=ZAZ=Z(AZ)"=ZZ"A"=ZZ"(AYA)"=Z(AZ)"(AY)" Z(AZ(AY)=ZAY =(ZA)"Y=A"Z"Y A"Z"(YAY) APZ(YA)"Y=A"Z A"YY=(AZA)Y"Y =A"YY =(YA)"Y=YAY=Y 即,满足四个Penrose方程的Z是唯一的」 该证明实际上给出了Moore-Penrose逆的一种构造方法。由A的 唯一性可知:(1)当A为满秩方阵时,A=A;(2)A实际上还是一 个限制相当严格,可考虑更加放宽。 3.{i,j,…,l}-逆的定义:A∈Cmx",若Z∈Cmxm且满足Penrose方程 中的第(i),(),…,()个方程,则称Z为A的{i,j,…,}-逆,记为 7
( ) ( ) ( )( ) ( )( ) ( ) ( ) ( ) ( ) ( ) H HH H H H H H HH H H HH H HHHH H H HH H Z ZAZ Z AZ ZZ A ZZ AYA Z AZ AY Z AZ AY ZAY ZA Y A Z Y A Z YAY A Z YA Y A Z A Y Y AZA Y Y A Y Y YA Y YAY Y = = = = = = = = = = = = = = = = = 即,满足四个 Penrose 方程的 Z 是唯一的. 该证明实际上给出了 Moore-Penrose 逆的一种构造方法。由 † A 的 唯一性可知:(1)当 A 为满秩方阵时, † 1 A A− = ; (2) † A 实际上还是一 个限制相当严格,可考虑更加放宽。 3. {ij l ,, , }-逆的定义: m n A C × ∀ ∈ ,若 n m Z C × ∈ 且满足 Penrose 方程 中的第( ),( ), ,( ) ij l 个方程,则称 Z 为 A 的{, , ,} ij l -逆,记为 7

A),其全体记为A{i,j,…,I。{i,j,…,1}-逆共有 C4+C?+C+C4=15类,但实际上常用的为如下5类: A{1,A{1,2,A{1,3},A{1,4},A{1,2,3,4}=A 二、{1}-逆的性质 引理:rank(AB)≤min(rankA,rank B) 证明:矩阵的秩=行秩=列秩 将A、B写成(A∈Cmx",B∈CmxP) 41 A= d21 02n =[a1a2…an] : am2 amn 8
(, , ,) ij l A ,其全体记为 Ai j l {, , ,} 。 {, , ,} ij l - 逆共有 1234 44 44 CCCC +++=15类,但实际上常用的为如下 5 类: A{1}, A{1,2}, A{1,3}, A{1,4}, A{1,2,3,4}= † A 二、{1}-逆的性质 引理: rank AB rankA rank B ( ) min ( , ) ≤ 证明:矩阵的秩=行秩=列秩. 将 ( , ) mn n p AB AC BC × × 、 写成 ∈ ∈ 11 12 1 21 22 2 1 2 1 2 [ ] n n n m m mn aa a aa a A aa a aa a = = 8

b b2 bip b b ba b2p b2 B= 三 bn2 bn. (1)设rank()=r,则必存在 4,a,…,4(,l2,…,,两两不同) 成为线性无关的向量组。所以,其它列向量α可表示为: a=∑Paa4=12,,)) 9
11 12 1 1 21 22 2 2 1 2 p p n n np n bb b b bb b b B bb b b = = (1)设rank A r ( ) = ,则必存在 1 2 1 2 , , , (, , , r ll l r a a a ll l 两两不同) 成为线性无关的向量组。所以,其它列向量 i a 可表示为: 1 ( 1,2, , ) k r i ik l k a pa i n = = ∑ = 9

bi AB=a a, …an] =[∑ba∑b,a…∑b,a] 可见AB 的各列向量均为41,4,…,4,的线性组合。亦即 rank(AB)≤r=rank(A (2) 同理。设rank(B)=s,则必存在b,b…,bn 成为线性无 关的向量组。所以,其它列向量b可表示为: 10
11 12 1 21 22 2 1 2 1 2 1 2 11 1 [ ] [ ] p p n n n np nn n i i i i ip i ii i bb b bb b AB a a a bb b ba ba ba = = = = = ∑∑ ∑ 可见 AB 的各列向量均为 1 2 ,,, r ll l aa a 的线性组合。亦即 rank AB r rank A ( ) () ≤ = (2) 同理。设rank B s ( ) = ,则必存在 1 2 , ,, mm ms bb b 成为线性无 关的向量组。所以,其它列向量 i b 可表示为: 10