
第十九讲 范数理论及其应用
第十九讲 范数理论及其应用 1

一、向量范数 范数可以看作长度概念的推广,主要用于逼近的程度。 1.向量范数定义:设V为数域K上的向量空间,若对于V的任一向量 x,对应一个实值函数,并满足以下三个条件: (1)非负性x20,等号当且仅当x=0时成立; (2)齐次性 lax=lalk,a∈k,x∈V; (3)三角不等式x+ysx+y,x,y∈V。 测称x为V中向量x的范数,简称为向量范数。 例1.X∈C",它可表示成x=[552…5],5:∈C, 2
一、向量范数 范数可以看作长度概念的推广,主要用于逼近的程度。 1. 向量范数定义:设 V 为数域 K 上的向量空间,若对于 V 的任一向量 x,对应一个实值函数 x ,并满足以下三个条件: (1)非负性 x 0 ≥ ,等号当且仅当 x=0 时成立; (2)齐次性 α = α α∈ ∈ x x , k, x V; (3)三角不等式 x y x y ,x,y V +≤ + ∈ 。 则称 x 为 V 中向量 x 的范数,简称为向量范数。 例 1. n x C∈ ,它可表示成 [ ] T 12 n x =ξ ξ ξ ,ξ ∈i C, 2

(2 就是一种范数 证明:D准数隆L-(②0, 当且仅当5=0(1=1,2,…,)时,即x=0时,x2=0 (ii)齐次性 ✉-(②-%(空r-al (i)y=[nn2…n]',n∈C x+y=[5+n52+n2…5n+n] k+y5=∑5+n 3
1 n 2 2 2 i i 1 x ∆ = = ξ ∑ 就是一种范数 证明:(i)非负性 1 n 2 2 2 i i 1 x 0 = =ξ ≥ ∑ , 当且仅当ξ= = i 0 i 1, 2, , n ( )时,即 x=0 时, 2 x =0 (ii)齐次性 1 1 n n 2 2 2 2 2 2 i i i 1 i 1 x x = = α = αξ = α ξ = α ∑ ∑ (iii) [ ] T 12 n y =η η η ,η ∈i C [ ] T 112 2 n n x y + = ξ +η ξ +η ξ +η n 2 2 2 i i i 1 x y = + = ξ +η ∑ 3
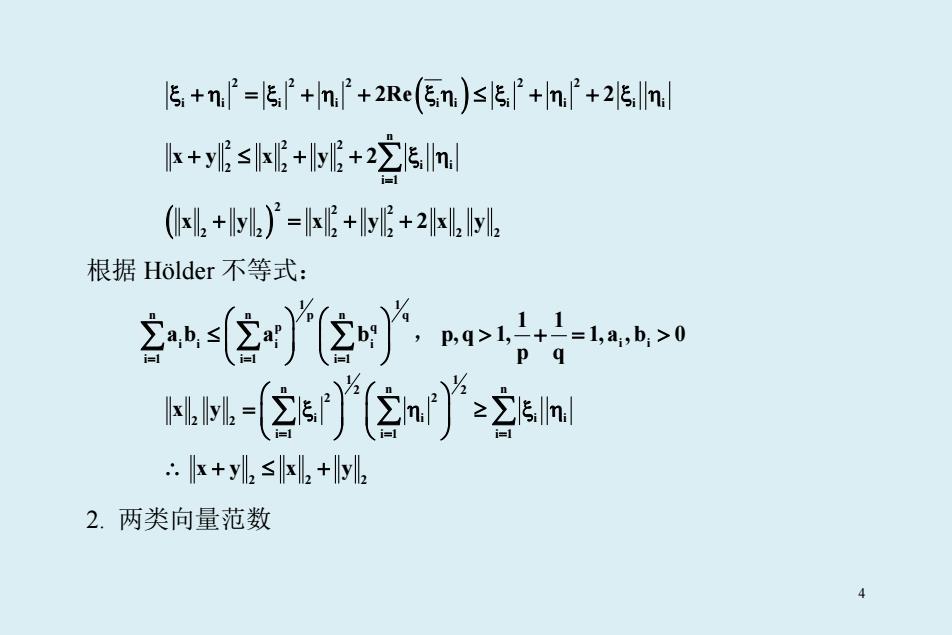
5+n=l5'+m+2Re(n)s5+n+25ml k+y6≤s+5+22lnl x,+y)=6+y6+2✉,ly 根据Holder不等式: 2空[2时:91片1a>0 p q M-(②s(②n≥2sml 小k+yL≤x+lyg 2.两类向量范数 4
( ) 222 2 2 i i i i ii i i i i ξ +η = ξ + η + ξη ≤ ξ + η + ξ η 2Re 2 n 222 222 i i i 1 xy x y 2 = + ≤ + + ξη ∑ ( ) 2 2 2 2 2 2 2 22 x y x y 2x y + =++ 根据 Hölder 不等式: 1 1 n nn p q p q ii i i i 1 i 1 i 1 ab a b = = = ≤ ∑∑∑ , i i 1 1 p,q 1, 1,a , b 0 p q > += > 1 1 nn n 2 2 2 2 2 2 i i i i i 1 i 1 i 1 x y = = = = ξ η ≥ ξη ∑∑ ∑ ∴ 222 xy x y +≤ + 2. 两类向量范数 4

(1),=(" 推广到小L=(Ax,A为厄米正定矩阵(椭圆范数) 当A=W=diag[w1w2…wn],w,>0 m.=它 加权范数 2)-(② (p≥1),称为向量的p-范数或1n范数。 证明:,显然满足非负性和齐次性 y=[nn,…n] N-(②rl-[②nryk+以-(②+n 5
(1) ( ) 1 H 2 2 x xx = 推广到 ( ) 1 H 2 A x x Ax = ,A 为厄米正定矩阵(椭圆范数) 当A W diag w w w = = [ 12 n ],w 0 i > 1 n 2 2 w i i i 1 x w= = ξ ∑ 加权范数 (2) 1 n p p p i i 1 x = = ξ ∑ (p≥1),称为向量的 p-范数或 pl 范数。 证明: p x 显然满足非负性和齐次性 [ ] T 12 n y =η η η 1 n p p p i i 1 x = = ξ ∑ , 1 n p p p i i 1 y = = η ∑ , 1 n p p p i i i 1 x y = + = ξ +η ∑ 5

(+y,”=2+nP=2+n+nl ≤2+n广+2+nnl 应用Holder不等式 25+n产2+n][② 2s+nn[2+n][空]形 (-q-P 6
( ) p n n p p 1 p ii ii ii i 1 i 1 n n p 1 p 1 ii i ii i i 1 i 1 x y − = = − − = = + = ξ +η = ξ +η ξ +η ≤ ξ +η ξ + ξ +η η ∑ ∑ ∑ ∑ 应用 Hölder 不等式 ( ) 1 1 nn n q p p 1 p 1q p ii i ii i i 1 i 1 i 1 − − = = = ξ +η ξ ≤ ξ +η ξ ∑∑∑ ( ) 1 1 nn n q p p 1 p 1q p ii i ii i i 1 i 1 i 1 − − = = = ξ +η η ≤ ξ +η η ∑∑∑ ( ) 1 1 1 p 1q p p q + =⇒ − = 6

东nr②[区-②n (②s+nr产s②sr必+{②nr 即k+y,≤,+yp 3.向量范数的等价性 定理1.设a、‖。为C的两种向量范数,则必定存在正数m、M,使 得ml。≤kp≤M小La,(m、M与x无关),它就称为向量范数的等价 性。 同时有,s.≤。 7
∴ 11 1 n n nn qp p p pp p ii ii i i i 1= i 1= i 1= i 1= ξ +η ≤ ξ +η ξ + η ∑ ∑ ∑∑ 111 n nn ppp ppp i i i i i 1= i 1= i 1= ξ +η ≤ ξ + η ∑ ∑∑ 即 ppp xy x y +≤ + 3. 向量范数的等价性 定理 1. 设 α、 β为 n C 的两种向量范数,则必定存在正数 m、M,使 得 mx x Mx αβ α ≤ ≤ ,(m、M 与 x 无关),它就称为向量范数的等价 性。 同时有 1 1 xx x M m βα β ≤ ≤ 7

二、矩阵范数 1.矩阵范数定义:设kmm(k=c或R)表示数域k上全体m×n阶矩阵的集 合。若对于km如中任一矩阵A,均对应一个实值函数,并满足以下四个 条件: (1)非负性:A≥0,等号当且仅当A=0时成立: (2)齐次性:IaA=A,a∈k; (3)三角不等式:A+B≤A+B,A,B∈k 则称A为广义矩阵范数; (4)相容性:AB≤AIB 则称A为矩阵范数。 8
二、矩阵范数 1. 矩阵范数定义:设 m n k (k c R) × = 或 表示数域 k 上全体m n × 阶矩阵的集 合。若对于 m n k × 中任一矩阵 A,均对应一个实值函数,并满足以下四个 条件: (1)非负性: A 0 ≥ ,等号当且仅当 A=0 时成立; (2)齐次性: α = α α∈ A A , k; (3)三角不等式: m n A B A B , A,B k × +≤ + ∈ 则称 A 为广义矩阵范数; (4)相容性: AB A B ≤ 则称 A 为矩阵范数。 8

2.常用的矩阵范数 )P范数:N,=na, A=(a)x为所有可能的向量,x=[5,5…5], al,=lal,Ad,=aA(ar儿(a≠o) ÷A,=A AlAxl 4-21,14-22a 9
2. 常用的矩阵范数 (1)p-范数: p p p Ax A max x = , ( ij )m n A a × = ,x 为所有可能的向量, [ ] T 12 n x =ξ ξ ξ , p p α =α x x , ( ) p p 1 Ax A x = α α (α ≠ 0) ∴ p p p x 1 A max Ax = = 1 1 1 x 1 A max Ax = = n 1 i i 1 x 1 = = ξ= ∑ , m n 1 ij j i1 j1 Ax a = = = ξ ∑ ∑ 9

可以证明:A,=∑A, 列(和)范数 1sism A2=V,(A"A) 谱范数 l≤i≤n AL=盟2a 行(和)范数 L-② =25 ISisn 4-② (2)Frobenius范数(F-范数)和导出性范数 10
可以证明: n 1 ij 1im i 1 A max a ≤ ≤ = = ∑ 列(和)范数 H 2 i 1in A max (A A) ≤ ≤ = λ 谱范数 n ij 1im j 1 A max a ∞ ≤ ≤ = = ∑ 行(和)范数 x ∞ = 1 n p p i i 1in i 1 p max ≤ ≤ = →∞ ξ =ξ ∑ 2 x = 1 n 2 2 i i 1= ξ ∑ (2)Frobenius 范数(F-范数)和导出性范数 10