
第7 第五章 定积分的物理在用 一、 变力沿直线所做的功 二、水压力 三、引力 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页 返回结束
目录 上页 下页 返回 结束 第7节 一、 变力沿直线所做的功 二、 水压力 三、 引力 定积分的物理应用 第五章

一、变力沿直线所做的功 1.变力做功 设物体在连续变力F(x)作用下沿x轴从x=α移动到 x=b,力的方向与运动方向平行,求变力所做的功 在[a,b]上任取子区间[x,x+dx],在其上所作的功元 素为 dw=F(x)dx a xx+dx乃 因此变力Fx)在区间[a,b]上所作的功为 w-["F(x)dx BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上 返回结束
目录 上页 下页 返回 结束 一、 变力沿直线所做的功 设物体在连续变力 F(x) 作用下沿 x 轴从 x a 移动到 力的方向与运动方向平行, 求变力所做的功 . a x x d x b x 在其上所作的功元 素为 dW F(x)dx 因此变力F(x) 在区间 上所作的功为 b a W F(x)dx 1.变力做功

例5.7.2在底面积为S的圆柱形容器中盛有一定量的气 体,由于气体的膨胀,把容器中的一个面积为S的活塞从 点α处移动到点b处(如图),求移动过程中气体压力所 做的功 解:建立坐标系如图.由波义耳一马略特定律知压强 p与体积V成反比,即p= v- 故作用在活塞上的 力为 F=p.S= X 功元素为 dW Fdx axx+dxh x X 所求功为 g-a=。-k如 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 返回 结束
目录 上页 下页 返回 结束 S 例5.7.2 体, 求移动过程中气体压力所 O x 解: 由于气体的膨胀, 把容器中的一个面积为S 的活塞从 点 a 处移动到点 b 处 (如图), 做的功. a b 建立坐标系如图. x x dx 由波义耳—马略特定律知压强 p 与体积 V 成反比 , 即 功元素为 故作用在活塞上的 所求功为 力为 在底面积为 S 的圆柱形容器中盛有一定量的气

2.抽水做功 例5.7.3有一半径为3m,高为5m的圆柱形蓄水桶,桶内 装满了水,求把桶内水全部抽出所做的功 解:建立坐标系如图.在任一小区间 [x,x+dx]上的一薄层水的重力为 5m 9.8π-32dxKN x+dx 这薄层水吸出桶外所作的功(功元素)为 dW=88.2元x-dx (kJ) 3 故所求功为 W=882元xdr= x 882z 设水的密 2 度为p ≈3461.85(KJ) BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 页 返回 结束
目录 上页 下页 返回 结束 3m 5m 例5.7.3 装满了水,求把桶内水全部抽出所做的功. 解: 建立坐标系如图. O x x x d x 在任一小区间 [x, x dx] 上的一薄层水的重力为 9.8π 3 dx 2 这薄层水吸出桶外所作的功(功元素)为 dW 88.2 π xdx (kJ) 故所求功为 5 0 W 88.2 π xdx 5 0 2 2 88.2 x 3461.85 ( KJ ) 设水的密 度为 (KN) 有一半径为3m,高为5m的圆柱形蓄水桶,桶内 2.抽水做功

二、水压力 设一薄板abAB铅直的放置在水中,求此薄板一侧所 受的水压力P 0 取水的深度x为积分变量, 它的变化区间为a,b],在区间 x+dx y=f(x) [a,b]上任取一小区间[x,x十dx], b 设水作用在此小区间上的相应的 小曲边梯形的压力为△P dP=压强×面积=gx·dx=gxf(x)dx. 水压力P为P=gxxd BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 页 返回 结束
目录 上页 下页 返回 结束 二、水压力 设一薄板abAB铅直的放置在水中,求此薄板一侧所 受的水压力P. dP 压强面积 gx ydx gxf(x)dx. 取水的深度x为积分变量, 它的变化区间为[a,b],在区间 [a,b]上任取一小区间[x,x+dx], 设水作用在此小区间上的相应的 小曲边梯形的压力为ΔP. : ( ) . b a 水压力P为 P g x f x dx
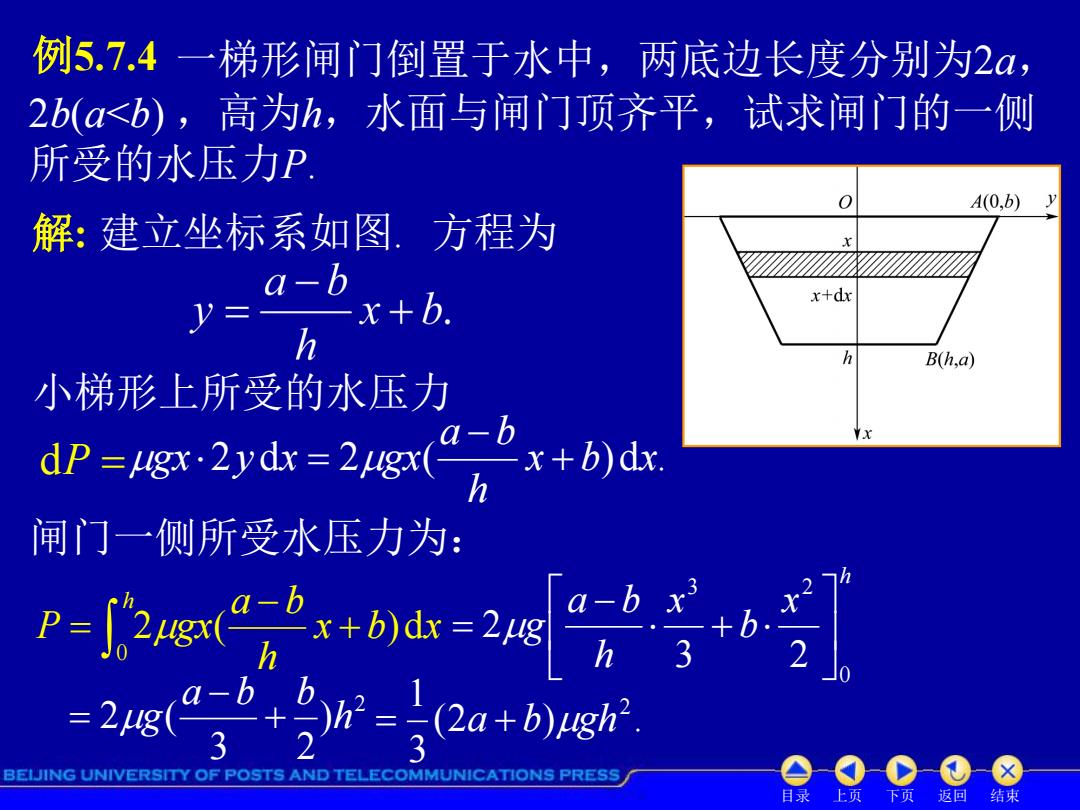
例5.7.4一梯形闸门倒置于水中,两底边长度分别为2a, 2b(a<b),高为h,水面与闸门顶齐平,试求闸门的一侧 所受的水压力P A(0,b) 解:建立坐标系如图.方程为 y a-b x+b. x+dx Bh,a) 小梯形上所受的水压力 dP-2yd=2x x+b)dx. 闸门一侧所受水压力为: P-P21gx(bx+bdx-2m 02 -2g+-2a+6 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页 下页返回 结束
目录 上页 下页 返回 结束 h x b x h a b g 0 3 2 3 2 2 例5.7.4 2b(a<b) ,高为h,水面与闸门顶齐平,试求闸门的一侧 所受的水压力P. 解: 建立坐标系如图. 小梯形上所受的水压力 h x b x h a b P gx 0 2 ( )d 2 d 2 ( x b)dx. h a b gx y x gx dP 闸门一侧所受水压力为: 方程为 一梯形闸门倒置于水中,两底边长度分别为2a, 2 ) 3 2 2 ( h a b b g (2 ) . 3 1 2 a b gh
三、引力 质量分别为m,M的质点,相距r, 二者间的引力: 大小:F=GmM 方向:沿两质点的连线 若考虑物体对质点的引力,则需用积分解决 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页 返回结束
目录 上页 下页 返回 结束 三、 引力 质量分别为 的质点 , 相距 r , m M r 二者间的引力 : 大小: 方向: 沿两质点的连线 若考虑物体对质点的引力, 则需用积分解决

例5.7.5设有一长度为1,线密度为p的均匀细直棒,在 其中垂线上距α单位处有一质量为m的质点M,试计算 该棒对质点的引力 解:建立坐标系如图.细棒上小段 M d F [x,x+dx]对质点的引力大小为 AF≈Gmedx d F a2+x2 故铅直分力元素为 x+dx x dFy=-dF.cosa =-G mpdx coSQ=-G- mpa 2+x2 dx, (a2+x2)月 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页 返回 结束
目录 上页 下页 返回 结束 例5.7.5 设有一长度为 l, 线密度为ρ 的均匀细直棒, 其中垂线上距 a 单位处有一质量为 m 的质点 M, M 该棒对质点的引力. 解: 建立坐标系如图. y 2 l 2 l [x, x d x] 细棒上小段 对质点的引力大小为 . d 2 2 a x m x F G 故铅直分力元素为 dFy dF cos a cos d 2 2 a x m x G d , ( ) 2 3 2 2 x a x m a G O x x 在 试计算 d F d Fx Fy d x d x

棒对质点的引力的铅直分力为 mpa dx dFy dF 2Gmpl a/4a2+72 x+dx x lx 棒对质点引力的水平分力F、=0 利用对称性 故棒对质点的引力大小为F=一 2Gmpl v4a2+P 方向与细棒垂直且由指向细棒中心. BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页 下页 返回结束
目录 上页 下页 返回 结束 利用对称性 x a x m a F G l y l d ( ) 2 2 2 3 2 2 - . 4 2 2 2 a a l Gm l 棒对质点引力的水平分力 0 . Fx . 4 2 2 2 a a l Gm l F 故棒对质点的引力大小为 棒对质点的引力的铅直分力为 M y 2 l 2 l a a O x x d F d Fx Fy d x d x 方向与细棒垂直且由M指向细棒中心

说明: 1)当细棒很长时,可视1为无穷大, b 此时引力大小为 2Gmp a 方向与细棒垂直且指向细棒 2)若考虑质点克服引力沿y轴从a处 移到b(a≤b)处时克服引力作的功 则有 x+dx X dw=-3 Gmpl dy 14)241 2G mpl F dy a 4a2+12 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页 返回 结束
目录 上页 下页 返回 结束 2 l O y 2 l a x x d x x 说明: a 2Gm 2) 若考虑质点克服引力沿 y 轴从 a 处 1) 当细棒很长时,可视 l 为无穷大 , 此时引力大小为 方向与细棒垂直且指向细棒 . 移到 b (a < b) 处时克服引力作的功, b y b a y y l y W Gm l 2 2 4 d 2 2 2 4 2 1 l G m l y y 则有 2 2 4 2 1 l G m l F a a