
第6为 第六章 空间曲线及其方程 空间曲线的方程 二、空间曲线在坐标面上的投影 三、空间立体图形的投影 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页 返回结束
目录 上页 下页 返回 结束 第六章 一、空间曲线的方程 二、空间曲线在坐标面上的投影 三、空间立体图形的投影 第6节 空间曲线及其方程

一、空间曲线的方程 1.空间曲线的一般式方程 空间曲线可视为两曲面的交线,其一般方程为方程组 F(x,y,z)=0 δ1 G(x,y,z)=0 Cj-0LFGy.5-0 例如,方程组 x2+y2=1 2x+3z=6 表示圆柱面与平面的交线C, BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 一、空间曲线的方程 空间曲线可视为两曲面的交线, 其一般方程为方程组 S2 G(x, y,z) 0 L F(x, y,z) 0 S1 例如,方程组 表示圆柱面与平面的交线 C. x z O 1 y C 2 1.空间曲线的一般式方程
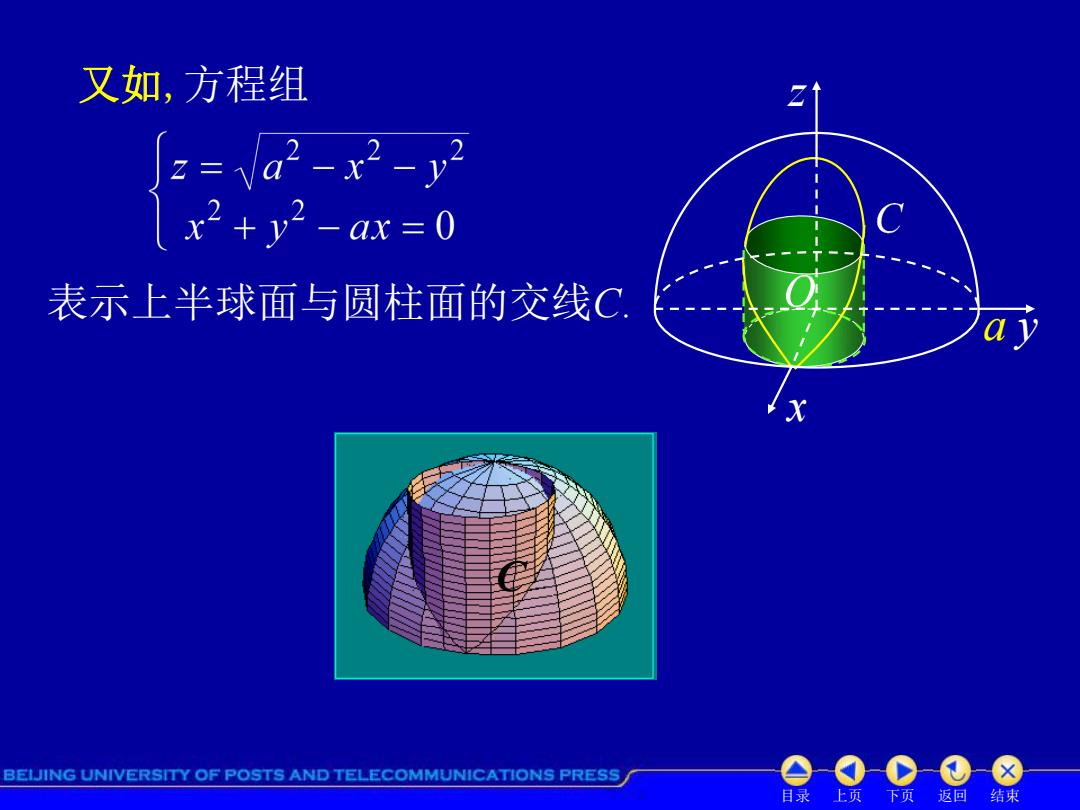
又如,方程组 Jz=Va2-x2-y2 x2+v2-ax=0 表示上半球面与圆柱面的交线C BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页 返回结束
目录 上页 下页 返回 结束 又如,方程组 表示上半球面与圆柱面的交线C. z y x a C

例6.6.1下面方程组表示怎样的曲线? x2+y2=1 3x+2z=6 解:方程组中第一个方程表示母线平行于z轴的圆柱 面,其准线是xOy面上的x2+y2=1;第二个方程表示 一个平行于轴的平面.因此方程组表示平面与圆柱面 的交线 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页 返回结束
目录 上页 下页 返回 结束 例6.6.1 下面方程组表示怎样的曲线? 解: 方程组中第一个方程表示母线平行于z轴的圆柱 面,其准线是xOy面上的 x 2+y 2=1;第二个方程表示 一个平行于y轴的平面.因此方程组表示平面与圆柱面 的交线

2.空间曲线的参数方程 将曲线C上的动点坐标x,y,表示成参数t的函数: x=x(t) y=y(t) 称它为空间曲线的 2=z(t) 参数方程 例如,圆柱螺旋线的参数方程为 x=acosot V y=asin0t令0=ot,b= acoso z =vt y asinO =b0 当0=2π时,上升高度h=2πb,称为螺距 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 上页 下页 返回 结束
目录 上页 下页 返回 结束 z y x O 将曲线C上的动点坐标 x, y, z表示成参数 t 的函数: 称它为空间曲线的 参数方程. 例如,圆柱螺旋线 v 令 t , b h 2πb 的参数方程为 上升高度 , 称为螺距 . M 2.空间曲线的参数方程

二、空间曲线在坐标面上的投影 设空间曲线C的一般方程为 F(x,y,2)=0 G(x,y,z)=0 消去z得投影柱面H(x,y)=0, 则C在xOy面上的投影曲线C'为 H(x,y)=0 2=0 消去x得C在yOz面上的投影曲线方程 R(y,2)=0 X x=0 T(x,z)=0 消去y得C在zOx面上的投影曲线方程 Y= BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 上页 返回 结束
目录 上页 下页 返回 结束 二、空间曲线在坐标面上的投影 设空间曲线C的一般方程为 消去 z 得投影柱面 则C在xOy 面上的投影曲线 C´为 消去 x 得C 在yOz 面上的投影曲线方程 消去y 得C在zOx 面上的投影曲线方程 0 ( , ) 0 z H x y 0 ( , ) 0 x R y z 0 ( , ) 0 y T x z z y x C C O

例如, c护21 在xOy面上的投影曲线方程为 22:30 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页 返回结束
目录 上页 下页 返回 结束 z y x 1 O C 例如, 在xOy 面上的投影曲线方程为 0 2 2 0 2 2 z x y y ( 1) ( 1) 1 1 : 2 2 2 2 2 2 x y z x y z C

又如, 上半球面 z=4-x2-y2和锥面z=3(x2+y2 所围的立体在xOy面上的投影区域为:二者交线在 xOy面上的投影曲线所围之域 二者交线 C:2=4-x2-y2 z=V3(x2+y2) 在xOy面上的投影曲线 x2+y2=1 1z=0 所围圆域:x2+y2≤1,z=0. BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页 下页 返回 结束
目录 上页 下页 返回 结束 z x 1 y 又如, 所围的立体在 xOy 面上的投影区域为: 上半球面 和锥面 在 xOy 面上的投影曲线 二者交线 1, 0. 2 2 所围圆域: x y z 二者交线在 xOy 面上的投影曲线所围之域 . C O

三、空间立体图形的投影 例6.6.5求由抛物面z=4(x2+y2)与平面z2所围成的 立体在xOy面上的投影 解将两个曲面方程联立, 得到交线C关于xOy面 的投影柱面方程为x2+y2 交线C在xOy面上的投影曲线为 z=0 这是xOy面上的一个圆,于是立体在xOy面上的投 影区域就是该圆在xO面上所围成的区域: x2+y2≤1/2 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 自录 返回 结束
目录 上页 下页 返回 结束 三、空间立体图形的投影 例6.6.5 求由抛物面z=4(x 2+y 2)与平面z=2所围成的 立体在xOy面上的投影. 解 将两个曲面方程联立,得到交线C关于xOy面 的投影柱面方程为 交线C在xOy面上的投影曲线为 这是xOy面上的一个圆,于是立体在xOy面上的投 影区域就是该圆在xOy面上所围成的区域: x 2+y 2≤1/2

内容小结 空间曲线的方程一三元方程组 或参数方程(如,圆柱螺线) ·空间曲线在坐标面上的投影 ·空间立体图形的投影 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页 返回结束
目录 上页 下页 返回 结束 内容小结 • 空间曲线的方程 三元方程组 或参数方程 • 空间曲线在坐标面上的投影 (如, 圆柱螺线) • 空间立体图形的投影