
第十五讲投影矩阵与Moore-Penrose逆
第十五讲 投影矩阵与 Moore-Penrose 逆 1

一、投影算子与投影矩阵 设L,M为C"的子空间并构成直和L+M=L⊕M=C".即 x∈C",唯一的y∈L,Z∈M使X=y+z 称y为x沿着M到L的投影。 1.定义:将任意x∈Cm变为其沿着M到L的投影的变换称为沿着M到 L的投影算子,记为P.M即P.MX=y∈L,投影算子是线性变换,其矩 阵称为投影矩阵,仍记为P.M。 2.充要条件 引理:设n阶方阵E为幂等矩阵,则N(E)=R(I-E) 证明: 2
一、投影算子与投影矩阵 设 L,M 为 n C 的子空间并构成直和 n LML MC + =⊕ = .即 n ∀ ∈x C ,∃唯一的y L,z M ∈ ∈ 使 x=y+z 称 y 为 x 沿着 M 到 L 的投影。 1. 定义:将任意 n x C∈ 变为其沿着 M 到 L 的投影的变换称为沿着 M 到 L 的投影算子,记为PL,M即P xyL L,M = ∈ ,投影算子是线性变换,其矩 阵称为投影矩阵,仍记为PL,M。 2. 充要条件 引理:设 n 阶方阵 E 为幂等矩阵,则N(E) R(I E) = − 证明: 2

:E2=E→E(I-E)=0→x∈C",E(I-E)x=0 →ER(I-E)]=0→R(I-E)sN(E) 另一方面x∈N(E),即Ex=0,则 x=Ix-0=Ix-Ex=(I-E)xER (I-E) →N(E)sR(I-E) ∴.N(E)=R(I-E) 定理:n阶方阵P成为投影矩阵的充要条件是P为幂等矩阵。 证明:充分性 P2=P,x∈C",令y=Px∈R(P),z=(I-P)x∈R(I-P)=N(P)。 若R(P)∩N(P)={0},则P=PRP,NP,确为投影矩阵,下面证之 Vx∈R(P)∩N(P), 3
2 n E E E(I E) O x C ,E[(I E)x] 0 E[R(I E)] 0 R(I E) N(E) = → − = →∀ ∈ − = → − =⇒ − ⊆ 另一方面∀ ∈x N(E),即Ex 0 = ,则 x Ix O Ix Ex (I E)x R I E NE RIE NE RIE = −= − =− ∈ − ⇒ ⊆− ∴ = − ( ) ( ) ( ) ( ) ( ) 定理:n 阶方阵 P 成为投影矩阵的充要条件是 P 为幂等矩阵。 证明:充分性 2 n P P, x C , y Px R(P),z (I P)x R I P N P = ∀∈ = ∈ = − ∈ − = 令 ( ) ( )。 若 R P N P 0, P P ( ) ( )= = { } 则 RP NP ( ), ( )确为投影矩阵,下面证之 ∀ ∈x R(P) N(P), 3

一方面,因x∈R(P),存在u∈C使x=Pu 另一方面x∈N(P),即Px=0.但Px=Pu=Pu=x→x=0 →R(P)∩N(P)={O}。 (P=I和P不等于I) 必要性P=PM故x∈C",唯一分解y∈L,z∈M使 x=y+z且Px=y →Px=Py=y=Px在意→P2=P y=y+0 3.投影矩阵的构造 设已知C"的子空间L、M构成直和L⊕M=C",下面构造P,M
一方面,因 n x R(P), u C x Pu ∈ ∈= 存在 使 { } 2 x N(P), Px 0. Px P u Pu x R(P) N(P) 0 P=I P I ∈ = = = =→ x 0 ⇒ = = 另一方面 即 但 。 ( 和 不等于 ) n 必要性 P P x C = ∀∈ ∃ ∈ ∈ L,M 故 , 唯一分解 y L,z M 使 x y z Px y =+ = 且 2 2 x P x Py y Px P P yy0 ↑ → = = = → = = + 任意 3. 投影矩阵的构造 设已知 n C 的子空间 L、M 构成直和 n L MC ⊕ = ,下面构造PL,M。 4

取L的一个基{各2x}(设L为r维子空间),M的一个基 2yn-r}(则M的维数为nr)。由直和关系知 {22yn-}即构成C的一个基。故,如令 X=[x,x2…x,],Y=[y1y2…yr] 则[XY]为可逆方阵。另一方面 X∈L→PLX,=Xiy,∈M-→P.My1=0 即B.M[XY]=[XO]→PM=[XO][XY]T 可见,PM的秩为r(rank(P.)=dimR(P)=dimL) 5
取 L 的一个基{x ,x x 12 r } (设 L 为 r 维子空间),M 的一个基 {y ,y y 12 nr − } ( 则 M 的维数为 n-r )。 由 直 和 关 系 知 {x ,x x y ,y y 12 r 12 nr ; − }即构成 n C 的一个基。故,如令 X x ,x x = 12 r ,Y y ,y y = 1 2 nr − 则[X Y]为可逆方阵。另一方面 i L,M i i i L,M i x L P x x ;y M P y 0 ∈→ = ∈ → = 即 [ ] [ ] [ ][ ] 1 P X Y X O P X O X Y L,M L,M − = →= 可见,PL,M的秩为 r(rank P dimR P dimL ( L,M)= ( L,M)= ) 5

二、正交投影算子与正交投影矩阵 L为C的子空间,其正交补空间={x(x,y)=0,x∈C",y∈L}(无 特别声明取x“y) 1.定义:设L是C的子空间,则称沿着到L的投影算子P为正 交投影算子,简记为P。正交投影算子的矩阵称为正交投影矩阵, 仍记为P。 2.充要条件:n阶方阵P为正交投影矩阵的充要条件是P为幂等的厄 米矩阵。 证明:首先证明两个引理: (1)对n阶方阵A,x∈C"均有xAx=0则A=0, 6
二、正交投影算子与正交投影矩阵 L 为 n C 的子空间,其正交补空间 { } n L x x y 0,x C ,y L ⊥ = =∈ ∈ ( , ) (无 特别声明取 Hx y ) 1. 定义:设 L 是 n C 的子空间,则称沿着L⊥ 到 L 的投影算子 L,L P ⊥ 为正 交投影算子,简记为PL 。正交投影算子的矩阵称为正交投影矩阵, 仍记为PL 。 2. 充要条件:n 阶方阵 P 为正交投影矩阵的充要条件是 P 为幂等的厄 米矩阵。 证明:首先证明两个引理: (1)对 n 阶方阵 A, n ∀ ∈x C 均有 Hx Ax 0 = 则 A=0, 6

(2)N(PH)=R(P) (1)证明:设A=(a)x取x=[00…l第个)…0]则x"Ax=ai=0 再取x=[00,50…0,5p00](i≠j),注意到a=0, 则xAX=5a5,+5a5, ,5=5,=1,则a+am=0 5,=1,5=V-1,则a与-a=0 →a)=ai=0统一考虑即A=0 (2)证明:x∈N(PH),即PHx=0→xP=0→ y∈C",x(Py)=0 由y的任意性,知x⊥R(P)→N(P)∈R(P) 另一方面,设X∈R+(P)即y∈C",均有xH(Py)=0→xP=0 7
(2)N( H P )=R P (⊥ ) (1)证明:设 A= [ ] T ij n n (a ) x 0 0 1 0 (i) × 取 = 第 个 则 H ii x Ax a 0 = = T i j ii H i ij j j ji i i j ij ji ij ji i j ij ji x 00 00 00 ij a 0 x Ax a a 1, a a 0 a a 0 A0 1, 1, a a 0 = ξξ ≠ = =ξ ξ +ξ ξ ξ =ξ = + = → →== = ξ= ξ= − − = 再取 , , , , ( ),注意到 , 则 则 统一考虑即 则 HH H n H H 2 x N(P ), P x 0 x P 0 y C x Py 0 y x RP NP RP ⊥ ∀ ∈ = → = → ∀∈ = ⊥⇒ ⊆ ( )证明: 即 , ( ) 由 的任意性,知 ( ) ( ) ( ) 另一方面,设 nH H x R (P) y C , x (Py) 0 x P 0 ⊥ ∈ ∀∈ 即 均有 = → = 7

→Px=0→x∈N(PH)→N(PH)2R(P) 所以N(PH)=R(P) 现在证明该充要条件。 充分性: P2=P,PH=P→P=PRp,Np)=PRp,N吗=PRp,R4p)=p) 必要性: P=PL xeC,可唯一地分解成y=Px∈L,z=(I-P)x∈L使x=y+z 又y∈L,z∈→y"z=0-→xpH(I-P)x=0年意→P(I-P)=0 PH=PP=(PP)H=(PH)H=P,P为厄米矩阵。 8
H H H P x 0 x N(P ) N(P ) R (P) → =→∈ ⇒ ⊇ ⊥ 所以 N( H P )=R P (⊥ ) 现在证明该充要条件。 充分性: H 2 H P PP P PP P P P Rp Np Rp Np Rp Rp ⊥ R p = =→= , ( ), ( )= ( ), ( )= = ( ), ( ) ( ) 必要性: L n P P x C, y Px L,z (I - P)x L x y z ⊥ = ∀ ∈ = ∈ = ∈ = + 可唯一地分解成 使 H H H x H y L,z L y z 0 x P (I P)x 0 P (I P) 0 ⊥ ∈ ∈ → = → − = → − = 又 任意 H H H H HH P P P (P P) (P ) P = = = = , P为厄米矩阵。 8

幂等已由上一定理得知。 3.正交投影矩阵的构造 设L的一个基为{1,2x},的一个基为{y,y2y}。则 xy1=0 令X=[x,x2…x]Y=[y1y2…y]则XY=0 (A-=(AA)A) 9
幂等已由上一定理得知。 3. 正交投影矩阵的构造 设 L 的一个基为{x ,x x 12 r } , L⊥ 的一个基为{y ,y y 1 2 nr − } 。则 H i j xy 0 = 令X x ,x x = 12 r ,Y y ,y y = 1 2 nr − 则 H XY 0 = 1 H 1H (A (A A) A ) − − = 9
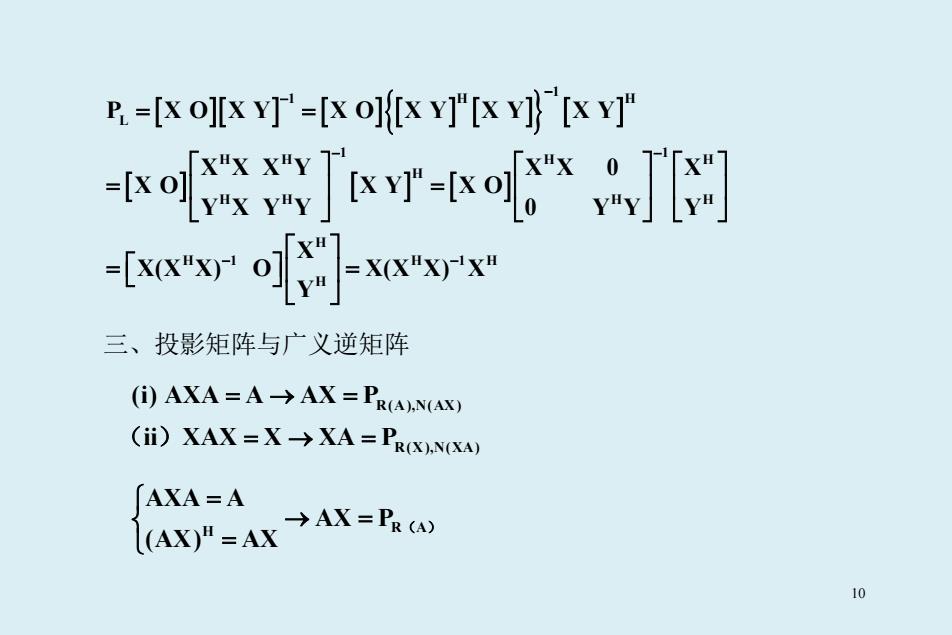
F.=[X O][X Y]=[X O][X Y]"[X Y][X Y]" -o [ro]wvrx 三、投影矩阵与广义逆矩阵 (①)AXA=A→AX=PR(A.NX (ii)XAX=X>XA PROX).NOXA) AXA=A 线(AX)P=AX→AX=Rw 10
[ ][ ] [ ]{[ ] [ ]} [ ] [ ] [ ] [ ] 1 1 HH L 1 1 H H H H H H H H H H H 1 H 1H H P X O X Y X O X Y X Y X Y X X X Y X X 0 X X O X Y X O Y X Y Y 0 Y Y Y X X(X X) O X(X X) X Y − − − − − − = = = = = = 三、投影矩阵与广义逆矩阵 R(A),N(AX) R(X),N(XA) (i) AXA A AX P ii XAX X XA P =→ = ( ) =→ = H R A AXA A AX P (AX) AX = → = = ( ) 10