
第四讲矩阵的对角化
第四讲 矩阵的对角化 1
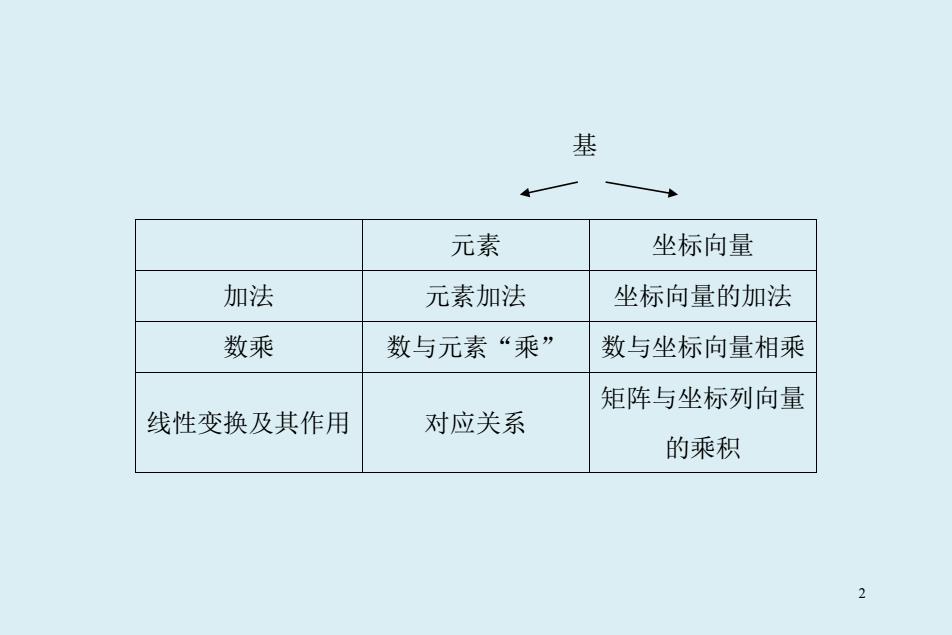
基 元素 坐标向量 加法 元素加法 坐标向量的加法 数乘 数与元素“乘” 数与坐标向量相乘 矩阵与坐标列向量 线性变换及其作用 对应关系 的乘积 2
基 元素 坐标向量 加法 元素加法 坐标向量的加法 数乘 数与元素“乘” 数与坐标向量相乘 线性变换及其作用 对应关系 矩阵与坐标列向量 的乘积 2

对任何线性空间,给定基后,我们对元素进行线性变换或线性运 算时,只需用元素的坐标向量以及线性变换的矩阵即可,因此,在后 面的内容中着重研究矩阵和向量。 3
对任何线性空间,给定基后,我们对元素进行线性变换或线性运 算时,只需用元素的坐标向量以及线性变换的矩阵即可,因此,在后 面的内容中着重研究矩阵和向量。 3

对角矩阵的形式比较简单,处理起来较方便,比如求解矩阵方程 Ax=b时,将矩阵A对角化后很容易得到方程的解。对角化的过程实 际上是一个去耦的过程。以前我们学习过相似变化对角化。那么,一 个方阵是否总可以通过相似变化将其对角化呢?或者对角化需要什么 样的条件呢?如果不能对角化,我们还可以做哪些处理使问题变得简 单呢?
对角矩阵的形式比较简单,处理起来较方便,比如求解矩阵方程 Ax b = 时,将矩阵 A对角化后很容易得到方程的解。对角化的过程实 际上是一个去耦的过程。以前我们学习过相似变化对角化。那么,一 个方阵是否总可以通过相似变化将其对角化呢?或者对角化需要什么 样的条件呢?如果不能对角化,我们还可以做哪些处理使问题变得简 单呢? 4

一、特征值与特征向量 1.定义:对m阶方阵A,若存在数入,及非零向量(列向量)x,使 得Ax=入x,则称入为A的特征值,x为A的属于特征值2的特 征向量。 ·特征向量不唯一 。特征向量非零 (λI-A)x=0有非零解,则det(2I-A)=0,称det(λI-A) 为A的特征多项式
一、 特征值与特征向量 1. 定义:对m阶方阵 A,若存在数λ ,及非零向量(列向量) x ,使 得 Ax x = λ ,则称λ 为 A的特征值,x为 A的属于特征值λ 的特 征向量。 • 特征向量不唯一 • 特征向量非零 • ( )0 λI Ax − = 有非零解,则det( ) 0 λI A − = ,称det( ) λI A − 为 A的特征多项式。 5

「122 [例1]A= 212,求其特征值和特征向量。 221 λ-1 -2 -2 [解] det(AI-4)=-2 2-1 -2 =0 -2 -2 2-1 (2+1)2(2-5)=0 九=九2=-1 儿3=5 属于特征值2=-1的特征向量 (-I-A)x=0 6
[例 1] 122 212 221 A = ,求其特征值和特征向量。 [解] 12 2 det( ) 2 1 2 0 22 1 I A −− − − =− − − = −− − λ λ λ λ 2 ( 1) ( 5) 0 λ λ + −= 1 2 λ λ = = −1 3 λ = 5 属于特征值λ = −1的特征向量 ( )0 −− = I Ax 6

「2 2 2 5=5 2 2 =0 5+52+53=0 5=52 2 2 25 53=-51-52 可取基础解系为 X1= H 属于入=5的特征向量 (5I-A)x=0 4 -2 -2 -2 4 -2 5 =0 51=52=5 -2 -2 45」 7
1 2 3 222 222 0 222 = ξ ξ ξ 123 ξξξ ++= 0 1 1 2 2 3 12 = = =− − ξ ξ ξ ξ ξ ξξ 可取基础解系为 1 1 0 1 x = − 2 0 1 1 x = − 属于λ = 5的特征向量 (5 ) 0 I Ax − = 1 2 3 4 22 24 2 0 2 24 − − − −= − − ξ ξ ξ ξξξ 123 = = 7

可取基础解系为 X3= 1 1 2.矩阵的迹与行列式 rA=∑a. 所有对角元素之和 i=1 detA=Π AA=∑ i=l 3.两个定理 (1)设A、B分别为m×n和n×m阶矩阵,则 8
可取基础解系为 3 1 1 1 x = 2. 矩阵的迹与行列式 1 tr n ii i A a = = ∑ 所有对角元素之和 1 det n i i A = =∏λ 1 tr n i i A = = ∑λ 3. 两个定理 (1)设 A、B分别为m n × 和n m× 阶矩阵,则 8

tr(AB)=tr(BA) (2)sylvster定理:设A、B分别为m×n和nxm阶矩阵,则 det(A-AB)=A"-"det(A-BA) 即:AB与BA的特征值只差零特征值的个数,非零特征值相同。 二、矩阵对角化的充要条件 定理:n阶方阵A可通过相似变换对角化的充要条件是它具有n个线性 无关的特征向量。 [证明]充分性:己知A具有n个线性无关的特征向量x,x2,…,xn,则 Ax =Ax i i=1,2,…,n 9
tr( ) tr( ) AB BA = (2)sylvster 定理:设 A、B分别为m n × 和n m× 阶矩阵,则 det( ) det( ) m n m n I AB I BA − λ λλ −= − 即:AB 与 BA 的特征值只差零特征值的个数,非零特征值相同。 二、 矩阵对角化的充要条件 定理:n阶方阵 A可通过相似变换对角化的充要条件是它具有n个线性 无关的特征向量。 [证明] 充分性:已知 A具有n个线性无关的特征向量 1 2 ,,, n xx x ,则 Ax x i ii = λ i n =1,2, , 9

A[x3…x]=[2xx2…x] 0 =[xx2…x] 2 0 元n x,x2,…,xn线性无关,故P=[x2…X]为满秩矩阵, [2 0 令Λ= M ,则有 An AP=PA 10
Ax x x x x x [ 1 2 n ] = [λλ λ 11 2 2 n n ] [ ] 1 2 1 2 0 0 n n xx x λ λ λ = 1 2 ,,, n xx x 线性无关,故P xx x = [ 1 2 n ]为满秩矩阵, 令 1 2 0 0 n λ λ λ Λ = ,则有 AP P = Λ 10