
第3章集合论 集合论是现代数学各分支的基础.是计算机科学许多理论不可或缺的工具.它起源于16 世纪末期,最初,人们为了追求微积分的坚实的基础,仅进行了数集的研究,直到1876一1883 年,德国数学家康托(Georg Cantor)发表了一系列有关集合论的文章,对任意元素的集合进 行了深入的探讨,提出了关于基数、序数和良序集等理论,奠定了集合论的深厚基础.19世 纪90年代后,集合论逐渐为数学家们采用,成为分析数学、代数和几何的有力工具.经过一 百多年的发展,集合论成为数学中发展最为迅速的分支之一 本章主要介绍集合论的初步知识,如集合的基本概念、运算、性质以及笛卡儿积等内容, 3.1 基本概念 1.集合的概念 集合是集合论中最基本的概念,很难给出精确的定义,只能给出说明性的描述.一般地, 把一些确定的,可以区分的事物放在一起构成的整体称为集合,简称集.构成集合的每个 事物称为集合的元素(或成员).构成集合的元素可以是具体的事物,也可以是抽象的事物, 例如: 方程x2-1=0的实数解集合 程序设计语言C的全部基本字符的集合 某高校全体学生的集合 坐标平面上所有点的集合 通常用大写的英文字母A,B,C,表示集合,用小写的英文字母a,b,c,表示元素.如 果元素a属于集合A,记作a∈A,读作“a属于A”.如果a不属于A,记作aEA或a年A, 读作“a不属于A”. 下面是几种特殊集合的表示符号: N—自然数集合(包括0). Z—整数集合,Z+—正整数集合,Z一负整数集合 Q—有理整数集合,Q+—正有理数集合,Q一负有理数集合 R—实数集合,R+—正实数集合,R一负实数集合 C—复数集合,等等 2.集合的表示方法 集合有多种表示方法,这里介绍几种常用的表示方法
第3章 集 合 论 集合论是现代数学各分支的基础, 是计算机科学许多理论不可或缺的工具. 它起源于 16 世纪末期, 最初, 人们为了追求微积分的坚实的基础, 仅进行了数集的研究, 直到 1876—1883 年, 德国数学家康托 (Georg Cantor) 发表了一系列有关集合论的文章, 对任意元素的集合进 行了深入的探讨, 提出了关于基数、序数和良序集等理论, 奠定了集合论的深厚基础. 19 世 纪 90 年代后, 集合论逐渐为数学家们采用, 成为分析数学、代数和几何的有力工具. 经过一 百多年的发展, 集合论成为数学中发展最为迅速的分支之一. 本章主要介绍集合论的初步知识, 如集合的基本概念、运算、性质以及笛卡儿积等内容. 3.1 基 本 概 念 1. 集合的概念 集合是集合论中最基本的概念, 很难给出精确的定义, 只能给出说明性的描述. 一般地, 把一些确定的, 可以区分的事物放在一起构成的整体称为集合, 简称集. 构成集合的每个 事物称为集合的元素 (或成员). 构成集合的元素可以是具体的事物, 也可以是抽象的事物. 例如: 方程 x 2 − 1 = 0 的实数解集合. 程序设计语言 C 的全部基本字符的集合. 某高校全体学生的集合. 坐标平面上所有点的集合. …… 通常用大写的英文字母 A, B, C, …表示集合, 用小写的英文字母 a, b, c, …表示元素. 如 果元素 a 属于集合 A, 记作 a ∈ A, 读作“a 属于 A”. 如果 a 不属于 A, 记作 a∈A 或 a 6∈ A, 读作“a 不属于 A”. 下面是几种特殊集合的表示符号: N——自然数集合 (包括 0). Z——整数集合, Z +——正整数集合, Z −——负整数集合. Q——有理整数集合, Q+——正有理数集合, Q−——负有理数集合. R——实数集合, R+——正实数集合, R−——负实数集合. C——复数集合, 等等. 2. 集合的表示方法 集合有多种表示方法, 这里介绍几种常用的表示方法

·44 第3章集合论 列元素法一把集合中的全部元素一一列举出来,元素之间用逗号“,”隔开,并把它们 用花括号“)”括起来.例如: A={1,2,3,4,5} 列元素法一般适合表示元素个数较少的集合.当集合中元素个数较多时,如果组成该集 合的元素有一定的规律,也可采用此方法,此时,列出部分元素,当看出组成该集合的其他元 素的规律时,其余元素用“”来表示.例如: B={1,2,3,,99} 此方法也可以表示含有无穷多个元素且元素有一定的规律的集合.例如: N={0,1,2,3,} 谓词表示法一一用谓词来概括集合中元素的属性.设x为某类对象的一般表示,P(x) 为关于x的一个命题,用{xP(z)}表示“使P(x)为真的全体x组成的集合”.例如,方程 x2-1=0的实数解集合可表示为C={xx∈RAx2-1=0}. 许多集合可以用两种方法来表示,如集合C也可以写成C={1,-1}.但是有些集合不 可以用列元素法表示,如实数集合R 文氏图表示法一一集合与集合的关系以及一些运算结果可以用文氏图形象地表示。在 给定的问题中,我们所考虑的所有事物的集合称为全集,记为E或U.在文氏图中,用矩形 表示全集;在矩形内部,用圆或其他形状的闭曲线表示全集的子集.不同的圆代表不同的集 合,并将运算结果得到的集合用阴影或斜线区域表示 需要注意的是,文氏图只是对某些集合间的关系及运算结果给出一种直观而形象的说 明,而不能用来证明。 全集中包含着我们讨论的所有事物.规定了全集后,我们讨论的任一集合中的所有元素 都属于全集.但全集是一个相对的概念,研究的问题不同,所取的全集也不同.例如,在研究 平面解析几何问题时,可以把整个平面取作全集:在初等数论中,可以把整数集Z作为全集 即使是同一个问题,也可以取不同的集合.例如,有关整数的问题,既可取Z为全集,也可取 Q或R为全集,但取Z为全集比取Q或R为全集显然要简便一些 3.元素与集合 对于元素与集合的理解,要注意以下几点: (1)组成一个集合的各个元素之间是彼此不同的,如果同一个元素在集合中多次出现,应 该认为是一个元素.例如: {1,1,2,4,2}={1,2,4} (2)集合的元素是无序的.例如: {1,2,3}={2,3,1 (3)任一元素(事物)是否属于一个集合,回答是确定的.也就是说,对于任意的元素α 和集合A,a∈A或a¢A必有一个成立. (4)集合的元素可以是任何事物,既可以是具体的事物,也可以是抽象的事物,还可以是 另外的集合.例如: {a,{1,2},p,{g}
· 44 · 第 3 章 集 合 论 列元素法——把集合中的全部元素一一列举出来, 元素之间用逗号“, ”隔开, 并把它们 用花括号“{}”括起来. 例如: A = {1, 2, 3, 4, 5} 列元素法一般适合表示元素个数较少的集合. 当集合中元素个数较多时, 如果组成该集 合的元素有一定的规律, 也可采用此方法, 此时, 列出部分元素, 当看出组成该集合的其他元 素的规律时, 其余元素用“…”来表示. 例如: B = {1, 2, 3, , 99} 此方法也可以表示含有无穷多个元素且元素有一定的规律的集合. 例如: N = {0, 1, 2, 3, }. 谓词表示法——用谓词来概括集合中元素的属性. 设 x 为某类对象的一般表示, P(x) 为关于 x 的一个命题, 用 {x| P(x)} 表示“使 P(x) 为真的全体 x 组成的集合”. 例如, 方程 x 2 − 1 = 0 的实数解集合可表示为 C = {x|x ∈ R ∧ x 2 − 1 = 0}. 许多集合可以用两种方法来表示, 如集合 C 也可以写成 C = {1, −1}. 但是有些集合不 可以用列元素法表示, 如实数集合 R. 文氏图表示法——集合与集合的关系以及一些运算结果可以用文氏图形象地表示。在 给定的问题中, 我们所考虑的所有事物的集合称为全集, 记为 E 或 U. 在文氏图中, 用矩形 表示全集; 在矩形内部, 用圆或其他形状的闭曲线表示全集的子集. 不同的圆代表不同的集 合, 并将运算结果得到的集合用阴影或斜线区域表示. 需要注意的是, 文氏图只是对某些集合间的关系及运算结果给出一种直观而形象的说 明, 而不能用来证明. 全集中包含着我们讨论的所有事物. 规定了全集后, 我们讨论的任一集合中的所有元素 都属于全集. 但全集是一个相对的概念, 研究的问题不同, 所取的全集也不同. 例如, 在研究 平面解析几何问题时, 可以把整个平面取作全集; 在初等数论中, 可以把整数集 Z 作为全集. 即使是同一个问题, 也可以取不同的集合. 例如, 有关整数的问题, 既可取 Z 为全集, 也可取 Q 或 R 为全集, 但取 Z 为全集比取 Q 或 R 为全集显然要简便一些. 3. 元素与集合 对于元素与集合的理解, 要注意以下几点: (1) 组成一个集合的各个元素之间是彼此不同的, 如果同一个元素在集合中多次出现, 应 该认为是一个元素. 例如: {1, 1, 2, 4, 2}={1, 2, 4} (2) 集合的元素是无序的. 例如: {1, 2, 3}={2, 3, 1} (3) 任一元素 (事物) 是否属于一个集合, 回答是确定的. 也就是说, 对于任意的元素 a 和集合 A, a ∈ A 或 a 6∈ A 必有一个成立. (4) 集合的元素可以是任何事物, 既可以是具体的事物, 也可以是抽象的事物, 还可以是 另外的集合. 例如: {a, {1, 2}, p, {q}}

3.2集合间的关系 .45· (⑤)元素和集合之间的关系是隶属关系,即属于或不属于,可以用一种树形图来表示这 种隶属关系,该图分层构成,每个层上的结点都表示一个集合,它的儿子就是它的元素.集合 S={a,{1,2},p,{g}的树形图如图3.1所示. {1,2 图3.1元素和集合间隶属关系的树形图 3.2 集合间的关系 在3.1节中,给出了“集合”“元素”以及元素与集合间的“属于”关系3个概念的直观 描述,以说明它们各自的含义.下面利用这3个概念定义集合间的关系 定义3.1设A、B是任意两个集合,如果A中的每一个元素都是B中的元素,则称 A是B的子集合,简称子集.也称A被B包含,或B包含A.记作A二B或B2A.符号 化表示为 A≤B台x(x∈A→x∈B) 如果A不被B包含,则记作A生B.符号化表示为 A4B÷3x(x∈AAx年B) 例如,A={a,b},B={a,b,c以,C={b,c,d,则有A二B,但A车C. 注意符号∈和二的区别,∈表示元素与集合间的“属于”关系,二表示集合间的“包含” 关系. 定义3.2设A,B是两个集合,如果ACB且BCA,则称A与B相等,记作A=B. 符号化表示为 A=B÷ACB且BCA 如果A与B不相等,则记作A≠B. 该定义给出了一个重要原则:要证明两个集合相等,唯一的方法就是证明每一个集合中 的任一元素均是另一个集合的元素. 定义3.3设A、B是两个集合,如果A是B的子集,而B中至少有一个元素不属于 A,则称A为B的真子集,记作ACB.符号化表示为 ACB台Hx(x∈A→x∈B)A3x(x∈BAx使A)】 或
3.2 集合间的关系 · 45 · (5) 元素和集合之间的关系是隶属关系, 即属于或不属于, 可以用一种树形图来表示这 种隶属关系, 该图分层构成, 每个层上的结点都表示一个集合, 它的儿子就是它的元素. 集合 S = {a, {1, 2}, p, {q}} 的树形图如图 3.1 所示. 图 3.1 元素和集合间隶属关系的树形图 3.2 集合间的关系 在 3.1 节中, 给出了“集合”“元素”以及元素与集合间的“属于”关系 3 个概念的直观 描述, 以说明它们各自的含义. 下面利用这 3 个概念定义集合间的关系. 定义 3.1 设 A、B 是任意两个集合, 如果 A 中的每一个元素都是 B 中的元素, 则称 A 是 B 的子集合, 简称子集. 也称 A 被 B 包含, 或 B 包含 A. 记作 A ⊆ B 或 B ⊇ A. 符号 化表示为 A ⊆ B ⇔ ∀x ( x ∈ A → x ∈ B) 如果 A 不被 B 包含, 则记作 A * B. 符号化表示为 A * B ⇔ ∃x ( x ∈ A ∧ x /∈ B) 例如, A = {a, b}, B = {a, b, c}, C = {b, c, d}, 则有 A ⊆ B, 但 A * C. 注意符号 ∈ 和 ⊆ 的区别, ∈ 表示元素与集合间的“属于”关系, ⊆ 表示集合间的“包含” 关系. 定义 3.2 设 A, B 是两个集合, 如果 A ⊆ B 且 B ⊆ A, 则称 A 与 B相等, 记作 A = B. 符号化表示为 A = B ⇔ A ⊆ B且B ⊆ A 如果 A 与 B 不相等, 则记作 A 6= B. 该定义给出了一个重要原则: 要证明两个集合相等, 唯一的方法就是证明每一个集合中 的任一元素均是另一个集合的元素. 定义 3.3 设 A、B 是两个集合, 如果 A 是 B 的子集, 而 B 中至少有一个元素不属于 A, 则称 A 为 B 的真子集, 记作 A ⊂ B. 符号化表示为 A ⊂ B ⇔ ∀x ( x ∈ A → x ∈ B) ∧ ∃x ( x ∈ B ∧ x /∈ A) 或

·46 第3章集合论 ACB台ACB∧A≠B 如果A不是B的真子集,则记作A¢B. 例如,集合{a,b}是{a,b,c的真子集,但{a,b,c和{b,c,d}都不是{a,b,c}的真子集。 集合与集合的关系可以用文氏图形象地表示,集合A和B的3种不同关系的文氏图如 图3.2所示 (a)ACB (b)AB (c)A=B 图3.2集合A和B的3种关系的文氏图 定义3.4不含任何元素的集合叫做空集,记作⑦.空集的符号化表示为 0={xx≠x} 例如,A={xz∈RAx2+2=0}是方程x2+2=0的实数解集,因为该方程无实数解, 所以A=②. 注意:0卡{0}. 定理3.1对于任意集合A,有 (1)aCA,且空集是唯一的:(2)ASA 证明:(1)假设⑦二A为假,则至少存在一个元素x,使x∈⑦且xA,因为空集⑦不 包含任何元素,所以这是不可能的. 设⑦1与⑦2都是空集,由上述结论可知,⑦1二⑦2且⑦2二⑦1,根据集合相等的定义得 01=⑦2,所以,空集是唯一的. (2)根据子集的定义可得,对于任意集合A,有A二A. 定义3.5含有n个元素的集合简称n元集,它的含有m(m≤n)个元素的子集叫做 它的m元子集. 任给一个n元集,如何求出它的全部子集呢?举例说明如下. 例3.1A={1,2,3},将A的子集分类 0元子集,也就是空集,只有一个:⑦ 1元子集,即单元集:{1},{2},{3}. 2元子集:{1,2},{1,3},{2,3}. 3元子集:{1,2,3. 一般地,对于n元集,它的m元子集有C个,所以不同的子集总数是 Co+CI+C2++Cn=2m
· 46 · 第 3 章 集 合 论 A ⊂ B ⇔ A ⊆ B ∧ A 6= B 如果 A 不是 B 的真子集, 则记作 A 6⊂ B. 例如, 集合 {a, b} 是 {a, b, c} 的真子集, 但 {a, b, c} 和 {b, c, d} 都不是 {a, b, c} 的真子集. 集合与集合的关系可以用文氏图形象地表示, 集合 A 和 B 的 3 种不同关系的文氏图如 图 3.2 所示. 图 3.2 集合 A 和 B 的 3 种关系的文氏图 定义 3.4 不含任何元素的集合叫做空集, 记作 ∅. 空集的符号化表示为 ∅ = {x| x 6= x} 例如, A = {x|x ∈ R ∧ x 2 + 2 = 0} 是方程 x 2 + 2 = 0 的实数解集, 因为该方程无实数解, 所以 A = ∅. 注意: ∅ 6= {∅}. 定理 3.1 对于任意集合 A, 有 (1)∅ ⊆ A, 且空集是唯一的; (2)A ⊆ A. 证明:(1) 假设 ∅ ⊆ A 为假, 则至少存在一个元素 x, 使 x ∈ ∅ 且 x 6∈ A, 因为空集 ∅ 不 包含任何元素, 所以这是不可能的. 设 ∅1 与 ∅2 都是空集, 由上述结论可知, ∅1 ⊆ ∅2 且 ∅2 ⊆ ∅1, 根据集合相等的定义得 ∅1 = ∅2, 所以, 空集是唯一的. (2) 根据子集的定义可得, 对于任意集合 A, 有 A ⊆ A. 定义 3.5 含有 n 个元素的集合简称 n 元集, 它的含有 m (m 6 n) 个元素的子集叫做 它的 m 元子集. 任给一个 n 元集, 如何求出它的全部子集呢? 举例说明如下. 例 3.1 A = {1, 2, 3}, 将 A 的子集分类: 0 元子集, 也就是空集, 只有一个: ∅. 1 元子集, 即单元集: {1},{2},{3}. 2 元子集: {1, 2},{1, 3},{2, 3}. 3 元子集: {1, 2, 3}. 一般地, 对于 n 元集, 它的 m 元子集有 C m n 个, 所以不同的子集总数是 C 0 n + C 1 n + C 2 n + + C n n = 2n

3.3集合的运算 .47. 3.3 集合的运算 3.3.1集合的基本运算 集合的运算,就是以集合为对象,按照确定的规则得到另外一些新集合的过程.集合的 基本运算有并、交、相对补、绝对补和对称差等 定义3.6设A、B是任意两个集合,由A或B中的元素构成的集合称为集合A与B 的并集,记作AUB. AUB={xx∈AVx∈B} 例如,A={1,2,4},B={2,4,5,则AUB={1,2,4,5. 集合的运算结果可以用文氏图形象地表示,集合A与B的并运算的文氏图表示如图3.3 所示 图3.3并运算的文氏图表示 两个集合的并运算可以推广到n个集合的并。 设A1,A2,,An是任意n个集合,则这n个集合的并可简记为UA,即 0A=ArUAU U4={r∈A1Vx∈AVVr∈An 并运算还可以推广到无穷多个集合的情况: UA:=A:UA2U UAU 定义3.7设A、B是任意两个集合,由既在A中又在B中的元素构成的集合称为集 合A与B的交集,记作A∩B. A∩B={xlx∈AAx∈B} 如果两个集合A、B的交集为空集,则称A、B不相交 例如,A={1,2,4,B={2,4,5},C={1,3},则A∩B={2,4,B∩C=⑦,所以B和 C是不相交的. 集合A与B的交运算的文氏图表示如图3.4所示 两个集合的交运算可以推广到n个集合的交
3.3 集合的运算 · 47 · 3.3 集合的运算 3.3.1 集合的基本运算 集合的运算, 就是以集合为对象, 按照确定的规则得到另外一些新集合的过程. 集合的 基本运算有并、交、相对补、绝对补和对称差等. 定义 3.6 设 A、B 是任意两个集合, 由 A 或 B 中的元素构成的集合称为集合 A 与 B 的并集, 记作 A S B. A S B = {x| x ∈ A ∨ x ∈ B} 例如, A = {1, 2, 4}, B = {2, 4, 5}, 则 A S B = {1, 2, 4, 5}. 集合的运算结果可以用文氏图形象地表示, 集合 A 与 B 的并运算的文氏图表示如图 3.3 所示. 图 3.3 并运算的文氏图表示 两个集合的并运算可以推广到 n 个集合的并. 设 A1, A2, , An 是任意 n 个集合, 则这 n 个集合的并可简记为 Sn i=1 Ai , 即 Sn i=1 Ai = A1 S A2 S S An = {x| x ∈ A1 ∨ x ∈ A2 ∨ ∨ x ∈ An} 并运算还可以推广到无穷多个集合的情况: S∞ i=1 Ai = A1 S A2 S S An S 定义 3.7 设 A、B 是任意两个集合, 由既在 A 中又在 B 中的元素构成的集合称为集 合 A 与 B 的交集, 记作 A T B. A T B = {x| x ∈ A ∧ x ∈ B} 如果两个集合 A、B 的交集为空集, 则称 A、B 不相交. 例如, A = {1, 2, 4}, B = {2, 4, 5}, C = {1, 3}, 则 A T B = {2, 4}, B T C = ∅, 所以 B 和 C 是不相交的. 集合 A 与 B 的交运算的文氏图表示如图 3.4 所示. 两个集合的交运算可以推广到 n 个集合的交
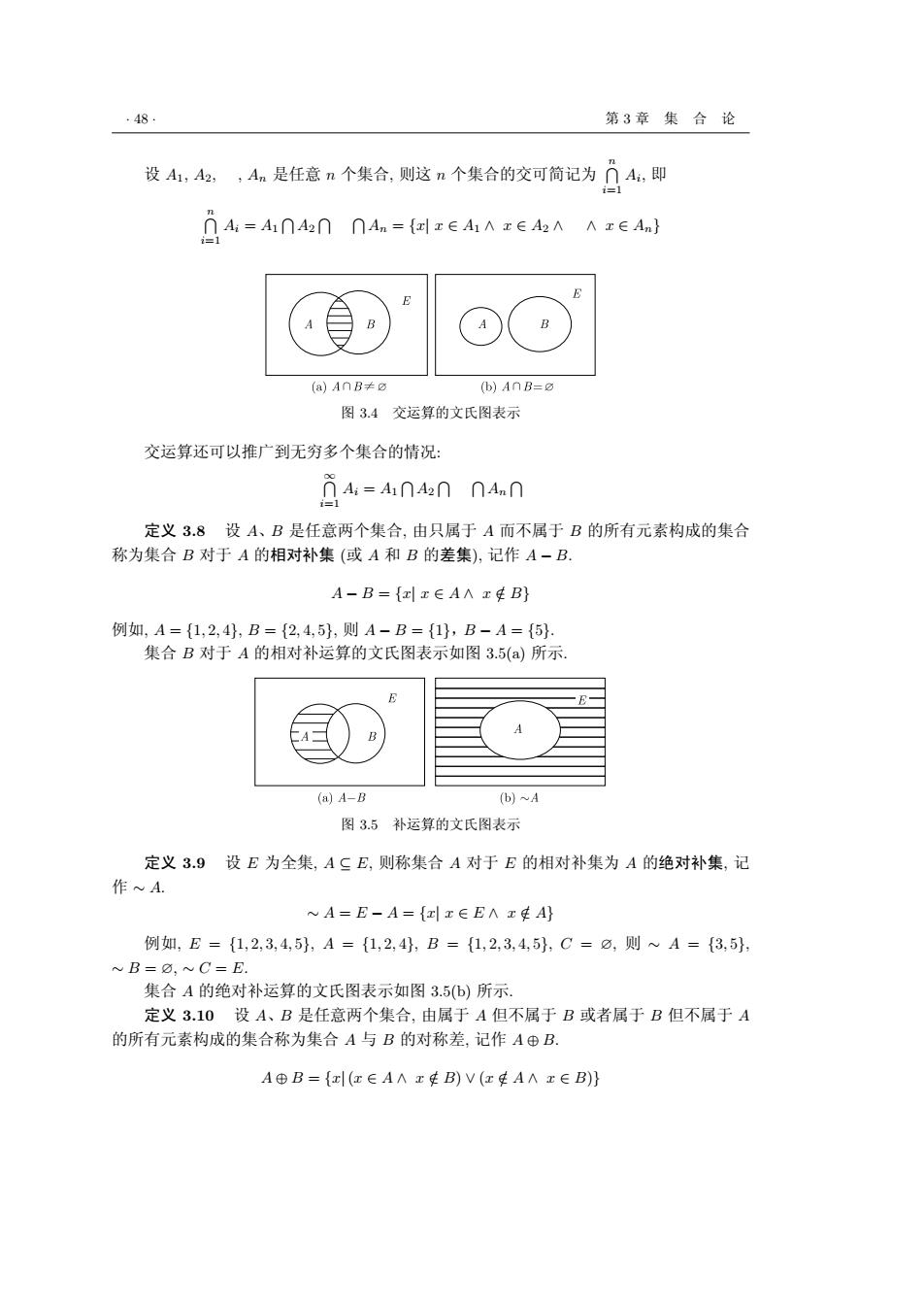
·48 第3章集合论 设A,4,,A是任意n个集合,则这n个集合的交可简记为凸A,即 I4=An4n∩An={z∈AZEAA A FEAn} E B (a)AnB≠a (b)AnB= 图3.4交运算的文氏图表示 交运算还可以推广到无穷多个集合的情况: A=A1∩42n∩4nn i=1 定义3.8设A、B是任意两个集合,由只属于A而不属于B的所有元素构成的集合 称为集合B对于A的相对补集(或A和B的差集),记作A-B. A-B={xx∈AAx年B} 例如,A={1,2,4,B={2,4,5},则A-B={1,B-A={5}. 集合B对于A的相对补运算的文氏图表示如图3.5(a)所示. (a)A-B (b)~A 图3.5补运算的文氏图表示 定义3.9设E为全集,A二E,则称集合A对于E的相对补集为A的绝对补集,记 作A. NA=E-A={xx∈EAx年A 例如,E={1,2,3,4,5},A={1,2,4,B={1,2,3,4,5},C=⑦,则~A={3,5} B=0~C=E. 集合A的绝对补运算的文氏图表示如图3.5(b)所示. 定义3.10设A、B是任意两个集合,由属于A但不属于B或者属于B但不属于A 的所有元素构成的集合称为集合A与B的对称差,记作A⊕B. A⊕B={x|(x∈AAx年B)V(x年AAx∈B)}
· 48 · 第 3 章 集 合 论 设 A1, A2, , An 是任意 n 个集合, 则这 n 个集合的交可简记为 Tn i=1 Ai , 即 Tn i=1 Ai = A1 T A2 T T An = {x| x ∈ A1 ∧ x ∈ A2 ∧ ∧ x ∈ An} 图 3.4 交运算的文氏图表示 交运算还可以推广到无穷多个集合的情况: T∞ i=1 Ai = A1 T A2 T T An T 定义 3.8 设 A、B 是任意两个集合, 由只属于 A 而不属于 B 的所有元素构成的集合 称为集合 B 对于 A 的相对补集 (或 A 和 B 的差集), 记作 A − B. A − B = {x| x ∈ A ∧ x /∈ B} 例如, A = {1, 2, 4}, B = {2, 4, 5}, 则 A − B = {1},B − A = {5}. 集合 B 对于 A 的相对补运算的文氏图表示如图 3.5(a) 所示. 图 3.5 补运算的文氏图表示 定义 3.9 设 E 为全集, A ⊆ E, 则称集合 A 对于 E 的相对补集为 A 的绝对补集, 记 作 ∼ A. ∼ A = E − A = {x| x ∈ E ∧ x /∈ A} 例如, E = {1, 2, 3, 4, 5}, A = {1, 2, 4}, B = {1, 2, 3, 4, 5}, C = ∅, 则 ∼ A = {3, 5}, ∼ B = ∅, ∼ C = E. 集合 A 的绝对补运算的文氏图表示如图 3.5(b) 所示. 定义 3.10 设 A、B 是任意两个集合, 由属于 A 但不属于 B 或者属于 B 但不属于 A 的所有元素构成的集合称为集合 A 与 B 的对称差, 记作 A ⊕ B. A ⊕ B = {x|(x ∈ A ∧ x /∈ B) ∨ (x /∈ A ∧ x ∈ B)}

3.3集合的运算 .49. 或 A⊕B=(A-B)八U(B-A) 集合A与B的对称差运算的文氏图表示如图3.6所示. 图3.6A⊕B的文氏图表示 例如,A={a,b,c,B={b,d,则A⊕B={a,c,d 从对称差的定义或文氏图容易看出 A⊕B=(AUB)-(A∩B) 该公式可作为A与B的对称差的一个等价定义. 设A、B、C为任意3个集合,对称差运算有以下性质: (1)A⊕B=B⊕A. (2)A⊕0=A. (3)A⊕A=0. (4)A⊕B=(A∩~B)U(~A∩B): (5)(A⊕B)⊕C=A⊕(B⊕C) (6)A∩(B⊕C)=(A∩B)⊕(A∩C) 3.3.2集合的运算律 集合运算同其他代数运算一样,都遵循一定的运算律.下面列出的是集合运算的主要运 算律,其中,E为全集,A、B、C为E的任意的3个子集 (1)幂等律 AUA=A,A∩A=A. (2)交换律 AUB=BUA,A∩B=B∩A (3)结合律 (AUB)UC=AU(BUC), (A∩B)∩C=A∩(B∩C) (4)分配律 AU(B∩C)=(AUB)∩(AUC), A∩(BUC)=(A∩B)U(A∩C). (⑤)吸收律 AU(A∩B)=A,A∩(AUB)=A (6)同一律 AU0=A,A∩E=A. (7)零律 AUE=E,A∩0=a. (8)排中律 AU~A=E. (⑨)矛盾律 A∩NA=0. (10)余补律 w⑦=E,E=⑦
3.3 集合的运算 · 49 · 或 A ⊕ B = (A − B) [ (B − A) 集合 A 与 B 的对称差运算的文氏图表示如图 3.6 所示. 图 3.6 A ⊕ B 的文氏图表示 例如, A = {a, b, c}, B = {b, d}, 则 A ⊕ B = {a, c, d}. 从对称差的定义或文氏图容易看出 A ⊕ B = (A S B) − (A T B) 该公式可作为 A 与 B 的对称差的一个等价定义. 设 A、B、C 为任意 3 个集合, 对称差运算有以下性质: (1) A ⊕ B = B ⊕ A. (2) A ⊕ ∅ = A. (3) A ⊕ A = ∅. (4) A ⊕ B = (A T ∼ B) S (∼ A T B). (5) (A ⊕ B) ⊕ C = A ⊕ (B ⊕ C). (6) A T (B ⊕ C) = (A T B) ⊕ (A T C). 3.3.2 集合的运算律 集合运算同其他代数运算一样, 都遵循一定的运算律. 下面列出的是集合运算的主要运 算律, 其中, E 为全集, A、B、C 为 E 的任意的 3 个子集. (1) 幂等律 A S A = A, A T A = A. (2) 交换律 A S B = B S A, A T B = B T A. (3) 结合律 (A S B) S C = A S (B S C), (A T B) T C = A T (B T C). (4) 分配律 A S (B T C) = (A S B) T (A S C), A T (B S C) = (A T B) S (A T C). (5) 吸收律 A S (A T B) = A, A T (A S B) = A. (6) 同一律 A S ∅ = A, A T E = A. (7) 零律 A S E = E, A T ∅ = ∅. (8) 排中律 A S ∼ A = E. (9) 矛盾律 A T ∼ A = ∅. (10) 余补律 ∼ ∅ = E, ∼ E = ∅

.50 第3章集合论 (11)双重否定律 (A)=A. (12)补交转换律 A-B=A∩B. (13)德·摩根律 ~(AUB)=~A∩~B, ~(A∩B)=~AUNB: A-(BUC)=(A-B)∩(A-C) A-(B∩C)=(A-B)U(A-C) 常称以上13组集合等式为集合恒等式, 证明集合等式常用的方法有两种: (1)逻辑公式等值演算法.证明的关键是要灵活运用逻辑基本等值式和集合运算的性质, 该方法证明的基本思想是:设P、Q为集合公式,根据集合相等的定义,要证P=Q,只 需证P二QAQCP为真.也就是要证对于任意的x有 x∈P台x∈Q (2)恒等代换法.该方法的实质就是利用集合运算的性质和己知的集合恒等式,把一个 集合用与之相等的集合代换,从而完成证明。 例3.2利用等值演算的方法证明下列恒等式: (1)分配律:AU(B∩C)=(AUB)∩(AUC). (2)排中律:AU~A=E. (3)德·摩根律:~(AUB)=~A∩~B. 证明:(1)对于任意的x,有 x∈AU(B∩C) ÷x∈AVx∈(B∩C) 台x∈AV(x∈BAx∈C) ÷(x∈AVx∈B)A(x∈AVx∈C) 台x∈(AUB)Ax∈(AUC) ÷x∈(AUB)∩(AUC) 所以,AU(B∩C)=(AUB)∩(AUC). (2)对于任意的x,有 x∈AUNA 台x∈AVx∈A 台x∈AVx年A 台x∈AVx∈A ÷1 台x∈E 所以,AU~A=E. (3)对于任意的x,有 x∈~(AUB) 台x(AUB)
· 50 · 第 3 章 集 合 论 (11) 双重否定律 ∼ (∼ A) = A. (12) 补交转换律 A − B = A T ∼ B. (13) 德 · 摩根律 ∼ (A S B) =∼ A T ∼ B, ∼ (A T B) =∼ A S ∼ B; A − (B S C) = (A − B) T (A − C), A − (B T C) = (A − B) S (A − C). 常称以上 13 组集合等式为集合恒等式. 证明集合等式常用的方法有两种: (1) 逻辑公式等值演算法. 证明的关键是要灵活运用逻辑基本等值式和集合运算的性质. 该方法证明的基本思想是: 设 P、Q 为集合公式, 根据集合相等的定义, 要证 P = Q, 只 需证 P ⊆ Q ∧ Q ⊆ P 为真. 也就是要证对于任意的 x 有 x ∈ P ⇔ x ∈ Q (2) 恒等代换法. 该方法的实质就是利用集合运算的性质和已知的集合恒等式, 把一个 集合用与之相等的集合代换, 从而完成证明. 例 3.2 利用等值演算的方法证明下列恒等式: (1) 分配律: A S (B T C) = (A S B) T (A S C). (2) 排中律: A S ∼ A = E. (3) 德 · 摩根律: ∼ (A S B) =∼ A T ∼ B. 证明:(1) 对于任意的 x, 有 x ∈ A S (B T C) ⇔ x ∈ A ∨ x ∈ (B T C) ⇔ x ∈ A ∨ (x ∈ B ∧ x ∈ C) ⇔ (x ∈ A ∨ x ∈ B) ∧ (x ∈ A ∨ x ∈ C) ⇔ x ∈ (A S B) ∧ x ∈ (A S C) ⇔ x ∈ (A S B) T (A S C) 所以, A S (B T C) = (A S B) T (A S C). (2) 对于任意的 x, 有 x ∈ A S ∼ A ⇔ x ∈ A ∨ x ∈∼ A ⇔ x ∈ A ∨ x /∈ A ⇔ x ∈ A ∨ ¬x ∈ A ⇔ 1 ⇔ x ∈ E 所以, A S ∼ A = E. (3) 对于任意的 x, 有 x ∈∼ (A S B) ⇔ x /∈ (A S B)

3.3集合的运算 51· 台(x走A)∧(x在B) ÷(x∈~A)A(x∈~B) 台x∈(~A∩NB) 所以,~(AUB)=~A∩~B 例3.3利用恒等代换的方法证明吸收律。 证明:AU(A∩B) =(A∩E)U(A∩B) =A∩(EUB) =A∩E =A 由同一律、分配律、零律等恒等式证明了吸收律第一式.用同样的方法可证吸收律第二 式,即A∩(AUB)=A. 除了以上集合等式以外,还有一些关于集合运算性质的重要结果 (14)A∩B≤A,A∩B≤B. (15)A∈AUB,B≤AUB (16)A-B≤A. (17)AB÷A∩B=A÷AUB=B÷A-B=0. 3.3.3例题 例3.4证明A-(B-C)=(A-B)U(A∩C) 证明:方法一.对于任意的x,有 x∈A-(B-C) ÷x∈A∧x生(B∩C) 台x∈AAx∈~(B∩~C) 台x∈A∧x∈(~BUC) 台x∈A∧(x∈BVx∈C) ÷x∈A∧(x生BVx∈C) 台(x∈AAx年B)V(x∈AAx∈C) 台x∈(A-B)U(A∩C) 所以,A-(B-C)=(A-B)U(A∩C) 方法二 A-(B-C) =A∩~(B∩~C) =A∩(~BUC) =(A∩~B)U(A∩C) =(A-B)U(A∩C) 例3.5设集合A、B满足条件A∩B=a,AUB=E,证明A=~B
3.3 集合的运算 · 51 · ⇔ (x /∈ A) ∧ (x /∈ B) ⇔ (x ∈∼ A) ∧ (x ∈∼ B) ⇔ x ∈ (∼ A T ∼ B) 所以, ∼ (A S B) =∼ A T ∼ B. 例 3.3 利用恒等代换的方法证明吸收律. 证明:A S (A T B) = (A T E) S (A T B) = A T (E S B) = A T E = A 由同一律、分配律、零律等恒等式证明了吸收律第一式. 用同样的方法可证吸收律第二 式, 即 A T (A S B) = A. 除了以上集合等式以外, 还有一些关于集合运算性质的重要结果. (14) A T B ⊆ A, A T B ⊆ B. (15) A ⊆ A S B, B ⊆ A S B. (16) A − B ⊆ A. (17) A ⊆ B ⇔ A T B = A ⇔ A S B = B ⇔ A − B = ∅. 3.3.3 例题 例 3.4 证明 A − (B − C) = (A − B) S (A T C). 证明:方法一. 对于任意的 x, 有 x ∈ A − (B − C) ⇔ x ∈ A ∧ x /∈ (B T ∼ C) ⇔ x ∈ A ∧ x ∈∼ (B T ∼ C) ⇔ x ∈ A ∧ x ∈ (∼ B S C) ⇔ x ∈ A ∧ (x ∈∼ B ∨ x ∈ C) ⇔ x ∈ A ∧ (x /∈ B ∨ x ∈ C) ⇔ (x ∈ A ∧ x /∈ B) ∨ (x ∈ A ∧ x ∈ C) ⇔ x ∈ (A − B) S (A T C) 所以, A − (B − C) = (A − B) S (A T C). 方法二. A − (B − C) = A T ∼ (B T ∼ C) = A T (∼ B S C) = (A T ∼ B) S (A T C) = (A − B) S (A T C) 例 3.5 设集合 A、B 满足条件 A T B = ∅, A S B = E, 证明 A =∼ B

·52 第3章集合论 证明:A=A∩E =A∩(BU~B) =(A∩B)U(A∩~B) =gU(A∩~B) =(B∩~B)U(A∩~B) =(BUA)∩~B =E∩~B =B 利用恒等代换不仅可以证明集合等式,还可以化简集合表达式. 例3.6化简下列集合表达式. (1)(B-(A∩C)U(A∩B∩C). (2)(AUBUC)∩(AUB)-(AUB-C)∩A). 解:(1)(B-(A∩C)U(A∩B∩C) =(B∩(A∩C)U(B∩(A∩C) =B∩(~(A∩C)UA∩C) =B∩E =B (2)因为AUB≤AUBUC,A≤AU(B-C),则有 (AUBUC)∩(AUB)-(AU(B-C)∩A) =(AUB)-A =(4UB)∩~A =(A∩~A)U(B∩~A) =gUB∩~A) =B-A 3.4 包含排斥原理 定义3.11设集合A={a1,a2,,an},它有n个不同元素,则称集合A的基数是n, 记作CardA=n或|Al=n. 基数是表示集合中所含元素多少的量.如果集合A的基数是n,这时称A为有限集.显 然,空集的基数是0,即|@=0.如果A不是有限集,则称A为无限集 现实生活中,经常会遇到对集合中的元素进行计数的问题,下面讨论的包含排斥原理是 个广泛使用的计数原理,可用来处理集合间含有公共元素的情况. 定理3.2(包含排斥原理)设A、B为有限集合,则 I4UB=|4+IB-A∩B 包含与排斥原理也称为容斥原理
· 52 · 第 3 章 集 合 论 证明:A = A T E = A T (B S ∼ B) = (A T B) S (A T ∼ B) = ∅ S (A T ∼ B) = (B T ∼ B) S (A T ∼ B) = (B S A) T ∼ B = E T ∼ B =∼ B 利用恒等代换不仅可以证明集合等式, 还可以化简集合表达式. 例 3.6 化简下列集合表达式. (1) (B − (A T C)) S (A T B T C). (2) ((A S B S C) T (A S B)) − ((A S (B − C) T A). 解:(1) (B − (A T C)) S (A T B T C) = (B T ∼ (A T C)) S (B T (A T C)) = B T (∼ (A T C) S (A T C)) = B T E = B (2) 因为 A S B ⊆ A S B S C, A ⊆ A S (B − C), 则有 ((A S B S C) T (A S B)) − (A S (B − C) T A) = (A S B) − A = (A S B) T ∼ A = (A T ∼ A) S (B T ∼ A) = ∅ S (B T ∼ A) = B − A 3.4 包含排斥原理 定义 3.11 设集合 A = {a1, a2, , an}, 它有 n 个不同元素, 则称集合 A 的基数是 n, 记作 CardA = n 或 |A| = n. 基数是表示集合中所含元素多少的量. 如果集合 A 的基数是 n, 这时称 A 为有限集. 显 然, 空集的基数是 0, 即 |∅| = 0. 如果 A 不是有限集, 则称 A 为无限集. 现实生活中, 经常会遇到对集合中的元素进行计数的问题, 下面讨论的包含排斥原理是 一个广泛使用的计数原理, 可用来处理集合间含有公共元素的情况. 定理 3.2 (包含排斥原理) 设 A、B 为有限集合, 则 |A S B| = |A| + |B| − |A T B| 包含与排斥原理也称为容斥原理