
第十八讲 全面最小二乘法
第十八讲 全面最小二乘法 1

一、法向回归 一组测量数据(,S),欲拟和直线 S=Ct+C2 2 最小二乘法采取目标函数:E(G,c2)=∑s,-ct,-c=min 它隐含了在测量中,,是精确测量的,只有S才测得不准确,而在 实际测量中,t,S都是无法准确测量的,因此,采用法向回归更有可 能。 2
一、 法向回归 一组测量数据( , ) i i t s ,欲拟和直线 1 2 s ct c = + 最小二乘法采取目标函数: ( ) 2 1 2 1 2 1 , min n i i i E c c s ct c = = −− = ∑ 它隐含了在测量中, i t 是精确测量的,只有 i s 才测得不准确,而在 实际测量中, i t , i s 都是无法准确测量的,因此,采用法向回归更有可 能。 2
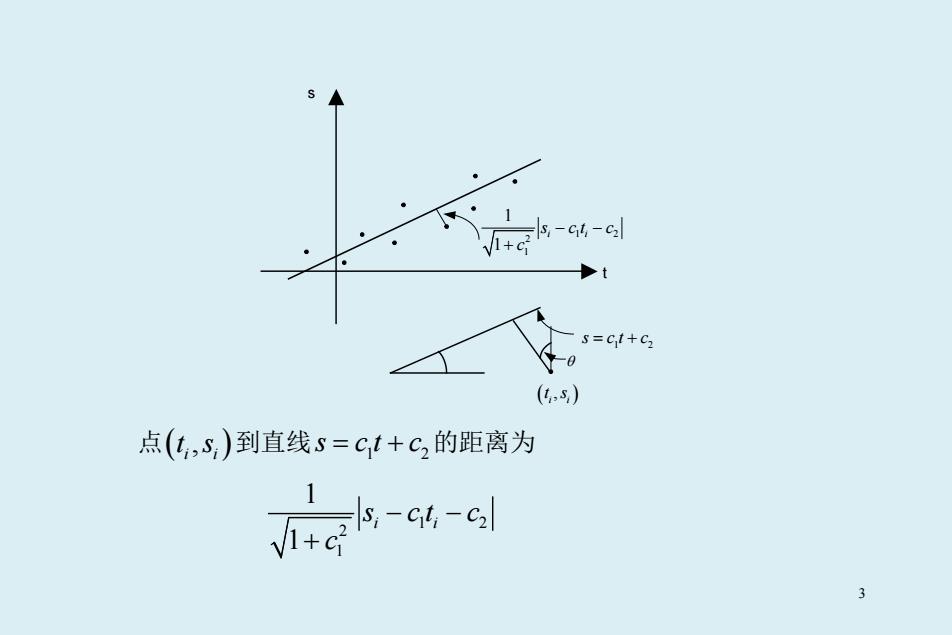
s,-ct,-cz t s=ct+C2 (4,) 点(,S)到直线s=ct+C,的距离为 以-d 3
1 2 2 1 1 1 i i s ct c c − − + t s θ 1 2 s ct c = + ( , ) i i t s 点( , ) i i t s 到直线 1 2 s ct c = + 的距离为 1 2 2 1 1 1 i i s ct c c − − + 3

故法向回归的目标函数为 aeeijg -c4,-c -min 1-2-26-6)=0之-4 OE OE 可立64280e-5-6l =22(e6s6c以-6) 4
故法向回归的目标函数为 ( ) 2 2 1 2 1 2 2 1 1 1 , min 1 n i i i E c c s ct c c = = −− = + ∑ ( )( ) 2 12 2 1 2 1 1 1 1 1 2 0 1 n n i i i i i i E s ct c c s ct c c = n = ∂ = − − − =→ = − ∂ + ∑ ∑ ( ) ( ) ( )( ) ( )( ) 2 1 2 1 2 2 1 2 2 1 1 1 1 1 2 12 1 1 2 1 1 2 2 1 1 2 1 n n i i ii i i i n ii i i i E c s ct c t s ct c c c c cc cs t s ct c c = = = ∂ = −− + − −− ∂ + + = − − −− + ∑ ∑ ∑ - 4
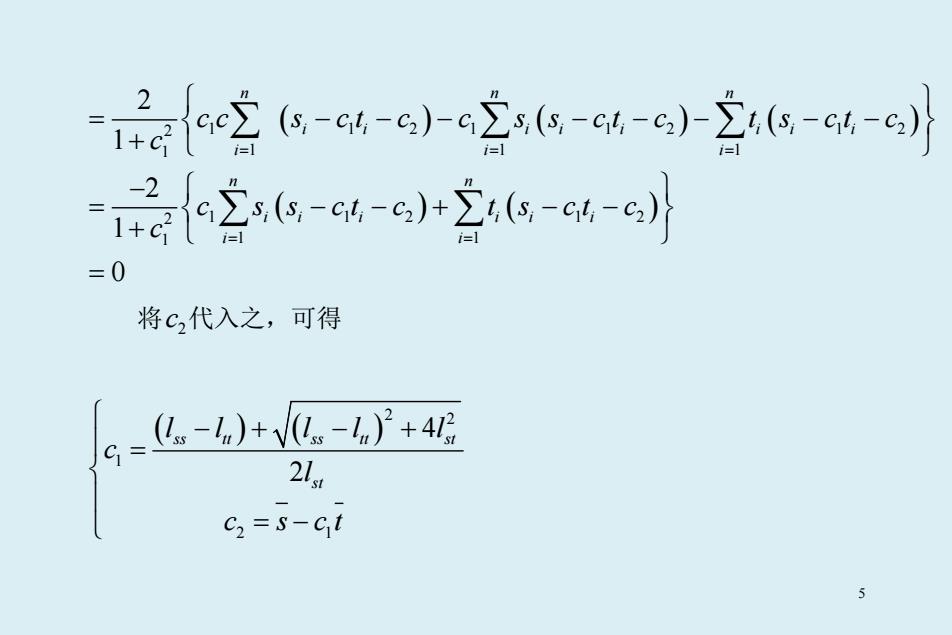
e空传-6)立g-e)aee} 12{空2a-6-o+e-c4-e} =0 将c2代入之,可得 _。-)+V。-)'+4 C 21. C2=s-Ct 5
( ) ( ) ( ) ( ) ( ) 2 1 1 21 1 2 1 2 1 1 11 2 1 12 1 2 1 1 1 2 1 2 1 0 n nn i i ii i ii i i ii n n ii i ii i i i cc s ct c c s s ct c t s ct c c c s s ct c t s ct c c = = = = = = −−− −−− −− + − = −−+ −− + = ∑ ∑∑ ∑ ∑ 将 2 c 代入之,可得 ( ) ( ) 2 2 1 2 1 4 2 ss tt ss tt st st ll ll l c l c s ct −+ − + = = − 5
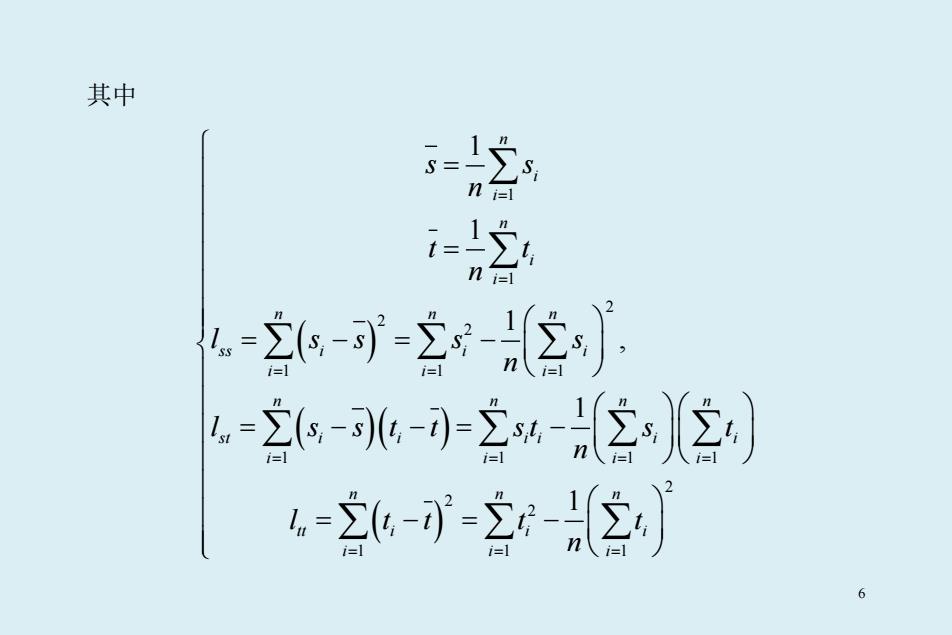
其中 5= S n n n --可-含2 -26-可-2w{2j2 ---立空 6
其中 ( ) ( ) ( ) ( ) 11 2 2 2 1 11 1 1 11 2 2 2 1 11 11 1 , 11 n i i n i i n nn ss i i i i ii n n nn st i i i i i i i i ii n nn tt i i i i ii s s n t t n l ss s s n l s s t t st s t n l tt t t n == = = = = = = = = = = = = = −= − = − −= − = −= − ∑∑ ∑ ∑∑ ∑ ∑ ∑∑ ∑ ∑∑ 6
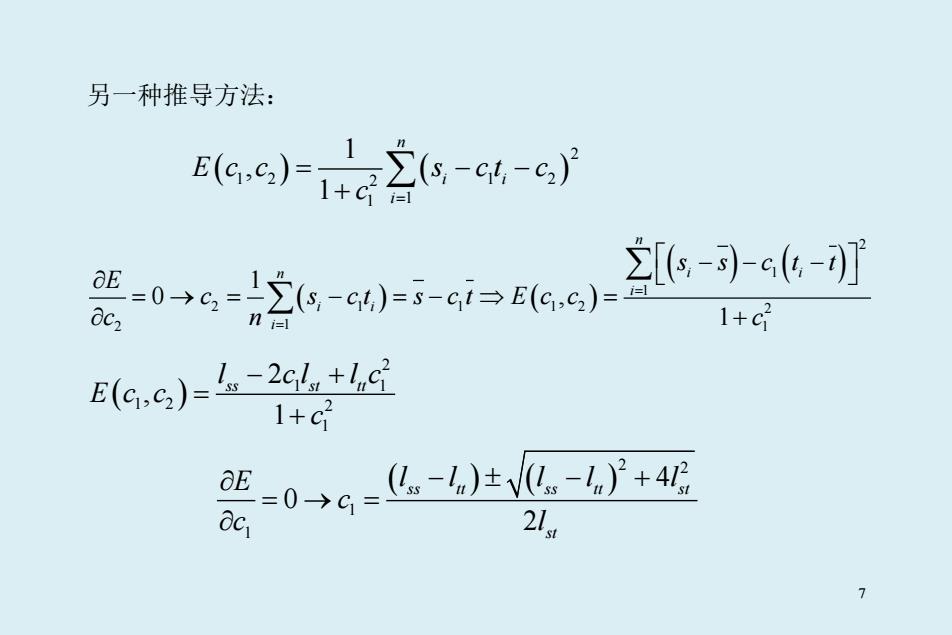
另一种推导方法: 86)4G2s-c4-6j =0→6=2s,-c4)-8-ci→E(4,9)=5 [(--c-刃 0c2 n i 1+c2 E(G,9)=。-2cl+c 1+c =0→G=么。-)±0。-+4 O 0C1 21 7
另一种推导方法: ( ) ( ) 2 1 2 2 1 2 1 1 1 , 1 n i i i E c c s ct c c = = −− + ∑ ( ) ( ) ( ) ( ) 2 1 1 2 1 1 12 2 2 1 1 1 0 , 1 n n i i i i i i s s ct t E c s ct s ct E c c c n c = = −− − ∂ =→ = − =− ⇒ = ∂ + ∑ ∑ ( ) 2 1 1 1 2 2 1 2 , 1 ss st tt l cl l c Ecc c − + = + ( ) ( ) 2 2 1 1 4 0 2 ss tt ss tt st st E ll ll l c c l ∂ −± − + =→ = ∂ 7

“土”中,“一”对应的E的最大值 作为比较,最小二乘法∑s-c4-cP=min给出 % C2=S-Ct 例1.7点测量 (t,5,)=(0,3.1),(0.5,3.9),(1,5.2),(1.5,6.0),(2,6.9),(2.5,8.0),(3.0,9.1) 拟合直线Ct+C2=S 解:计算结果t=1.5,s≈6.02857,ln=7,l=27.8743,1,=13.95 8
“±”中,“-”对应的 E 的最大值 作为比较,最小二乘法 2 1 2 1 min n i i i s ct c = ∑ −− = 给出 1 2 1 st tt l c l c s ct = = − 例1. 7 点测量 ( , 0,3.1 , 0.5,3.9 , 1,5.2 , 1.5,6.0 , 2,6.9 , 2.5,8 ) ( ) ( ) ( ) ( ) ( ) ( .0 , 3.0,9.1 ) ( ) i i t s = 拟合直线 1 2 ct c s + = 解:计算结果 1.5, 6.02857, 7, 27.8743, 13.95 tt ss st t s ll l = ≈ == = 8

最小二乘法给出c=1.99286,c,=3.03929 全面最小二乘法(法向回归)给出G1=1.99709,c2=3.03293 测量数据误差小,分布合理时,两种方法效果非常接近。 二、全面最小二乘法(Totally Least Square Method) 当方程Ax=b成为矛盾方程时,采用最小二乘法求解的观点实际 上认为b存在误差,而A不存在误差,故应有ε,使得 Ax=b+8 应尽量小以使得不至于严重得破坏方程→s2=min 全面最小二乘法采取如下观点解决矛盾方程的问题,不仅b存在 误差,A也存在误差,故,存在E和8,使 9
最小二乘法给出 1 2 c c = = 1.99286, 3.03929 全面最小二乘法(法向回归)给出 1 2 c c = = 1.99709, 3.03293 测量数据误差小,分布合理时,两种方法效果非常接近。 二 、全面最小二乘法(Totally Least Square Method) 当方程 Ax b = 成为矛盾方程时,采用最小二乘法求解的观点实际 上认为 b 存在误差,而 A 不存在误差,故应有ε ,使得 Ax b = + ε ε 应尽量小以使得不至于严重得破坏方程→ = ε 2 min 全面最小二乘法采取如下观点解决矛盾方程的问题,不仅 b 存在 误差,A 也存在误差,故,存在 E 和ε ,使 9

(A+E)x=b+8 E、£也应该尽量小,以使得不至于严重偏离原方程 →[Elc]le=min (+:-6+cea创+E1s]-0 c-4A-小-[ 则全面最小二乘解即求如下方程 (C+A)v=0 的非零解v,且v的最后分量不能为零,而其中△应满足△s=min 引理:设X∈C,m”,且存在奇异值分解, 10
( A Ex b + =+ ) ε E、ε 也应该尽量小,以使得不至于严重偏离原方程 [ | min ] F → = E ε ( ) ([ || 0 ] [ ]) 1 x A Ex b Ab E ε ε + =+⇔ + = − 记 [ |, |, ] [ ] 1 x C Ab E v ε = ∆= = − ,则全面最小二乘解即求如下方程 (C v +∆ = ) 0 的非零解 v,且 v 的最后分量不能为零,而其中∆应满足 min F ∆ = 引理:设 m n X Cr × ∈ ,且存在奇异值分解, 10