
第二十一讲广义特征值与极小极大原理
第二十一讲 广义特征值与极小极大原理 1

一、广义特征值问题 1、定义:设A、B为n阶方阵,若存在数,,使得方程Ax=入Bx存在 非零解,则称入为A相对于B的广义特征值,x为A相对于B的属于 广义特征值,的特征向量。 。是标准特征值问题的推广,当B=I(单位矩阵)时,广义特征值 问题退化为标准特征值问题。 ●特征向量是非零的 ●广义特征值的求解 (A-B)x=0或者(2B-A)x=0 2
一、 广义特征值问题 1、定义:设 A、B 为 n 阶方阵,若存在数λ ,使得方程Ax Bx = λ 存在 非零解,则称λ 为 A 相对于 B 的广义特征值,x 为 A 相对于 B 的属于 广义特征值λ 的特征向量。 ●是标准特征值问题的推广,当 B=I(单位矩阵)时,广义特征值 问题退化为标准特征值问题。 ●特征向量是非零的 ●广义特征值的求解 (A Bx 0 −λ = ) 或者 (λ− = B Ax 0 ) 2

→特征方程dt(A-入B)=0 求得入后代回原方程Ax=入Bx可求出x 本课程进一步考虑A、B厄米且为正定矩阵的情况。 2、等价表述 (1)B正定,B存在→BAx=入x,广义特征值问题化为了标准 特征值问题,但一般来说,BA一般不再是厄米矩阵。 (2)B厄米,存在Cholesky分解,B=GGH,G满秩 Ax=AGGx 令G"x=y 则 G-A(G")y=Ay 也成为标准特征值问题。 3
→ 特征方程 det A B 0 ( −λ =) 求得λ 后代回原方程Ax Bx = λ 可求出 x 本课程进一步考虑 A、B 厄米且为正定矩阵的情况。 2、等价表述 (1)B 正定, 1 B− 存在 → 1 B Ax x − = λ ,广义特征值问题化为了标准 特征值问题,但一般来说, 1 B A− 一般不再是厄米矩阵。 (2)B 厄米,存在 Cholesky 分解, H B GG = ,G 满秩 H Ax GG x = λ 令 H Gx y = 则 ( ) 1 1 H G AG y y − − = λ 也成为标准特征值问题。 3

GA(G)厂为厄米矩阵,广义特征值是实数,可以按大小顺序排 列入1≤入2≤…≤入。,一定存在一组正交归一的特征向量,即存在 y1y2…,y.满足 G-A(G")y:=Ay -8-0 还原为x=(G)y(1,2…,n,则 4
( ) 1 1 H G AG − − 为厄米矩阵,广义特征值是实数,可以按大小顺序排 列 λ ≤λ ≤ ≤λ 12 n ,一定存在一组正交归一的特征向量,即存在 12 n y ,y ,y 满足 ( ) 1 1 H G AG y y i i − − = λ H i j ij 1 ij y y 0 ij = =δ = ≠ 还原为 ( ) 1 H i i xG y − = (i=1,2,,n),则 4

,=(cc=,=8,-日 i=j (带权正交) i≠j 二、瑞利商 AB为n阶E米矩阵,瓦B正宽,彩()-一心K0)为A 相对于B的瑞利商。 设,X,为A相对于B的广义特征值和特征向量,且入≤2≤··≤ λ X1,X2…,Xn线性无关,所以,x∈C",存在a1,a2…,an∈C, 5
( )( ) H HH H i j i j i j ij 1 ij y y x G G x x Bx 0 ij = = = =δ = ≠ (带权正交) 二、 瑞利商 A、B 为 n 阶厄米矩阵,且 B 正定,称 ( ) ( ) H H x Ax Rx x 0 x Bx = ≠ 为 A 相对于 B 的瑞利商。 设 λi, i x 为 A 相对于 B 的广义特征值和特征向量,且 λ1≤λ2≤···≤ λn 12 n x ,x ,x 线性无关,所以, n ∀ ∈x C ,存在 12 n a ,a ,a C ∈ , 5

使得 X= i=1 -[空八含空a2 "Ax-xx xla .R()=豆 a 以下两点成立 6
使得 n i i i 1 x ax = = ∑ H n nn n H H 2 i i i j j ji j i i 1 j 1 i,j 1 i 1 x Bx a x B a x a a x Bx a = = = = = = = ∑ ∑∑ ∑ nn n HH H 2 i i ji j ji i j i i i,j 1 i,j 1 i 1 x Ax a a x Ax a a x Bx a = = = = = λ =λ ∑∑ ∑ ∴ ( ) n 2 i i i 1 n 2 i i 1 a R x a = = λ = ∑ ∑ 以下两点成立 6

minR(x)=M maxR()=入. 证明:R(-”A k为非零常数 x"Bx (kx)"B(kx) 可取k=有k= AR(冈= XHAX (闭区域) 当X=X1或a=0(i=2,3,…,n)时,R()=入 7
● ( ) 1 x 0 minR x ≠ = λ ( ) n x 0 max R x ≠ = λ 证明: ( ) ( ) ( ) ( ) ( ) H H H H x Ax kx A kx R x x Bx kx B kx = = k 为非零常数 可取 1 k x = , kx 1 = ∴ ( ) H H x 1 x Ax R x x Bx = = (闭区域) 当 1 x x = 或a 0 i 2, 3, , n i = = ( ) 时,R x( ) = λ1 7
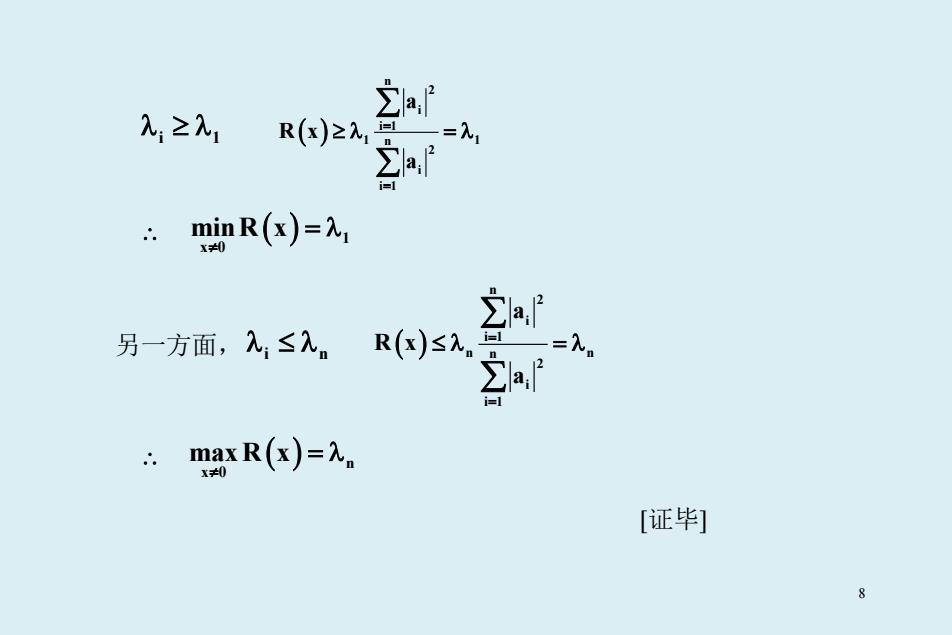
入2入1R()2台 2= minR(x)= 另一方面,2≤入。1 )SA —=入。 2 :maxR()=。 [证毕] 8
λ ≥λ i 1 ( ) n 2 i i 1 1 1 n 2 i i 1 a R x a = = ≥λ =λ ∑ ∑ ∴ ( ) 1 x 0 minR x ≠ = λ 另一方面,λ ≤λ i n ( ) n 2 i i 1 n n n 2 i i 1 a R x a = = ≤λ =λ ∑ ∑ ∴ ( ) n x 0 max R x ≠ = λ [证毕] 8

当B=I时,标准特征值问题 AX=)x(AH=A〉 21≤2≤…≤1n 1xx=δg 则 脚发 max 进一步分析可得 咖R(。=方 R(l=入 R(=入maR(闪=久 9
当 B=I 时,标准特征值问题 Ax x = λ ( H A A= ) 12 n H i j ij x x λ ≤λ ≤ ≤λ = δ 则 ( ) H H 1 x 0 x Ax min ≠ x x = λ ( ) H H n x 0 x Ax max ≠ x x = λ 进一步分析可得 ( ) 1 2 x 0 a 0 minR x ≠ = = λ ( ) n n 1 x 0 a 0 max R x − ≠ = = λ ( ) 12 k k 1 x 0 aa a 0 minR x + ≠ = = = = = λ ( ) n n1 nk nk1 x 0 aa a 0 max R x − − − − ≠ = = = = = λ 9

定理1.设L=span{X,X1,,X}(亿,≤+1≤…≤入),则 minR()=入. maxR(x)=, x∈L 这一结果不便于应用,希望对上述结果进行改造,改造成不依赖 于x的一种表达方式。 a1=0和a.=0的情况均对应于x在(n-1)维的子空间内变动,x 在L中变动是在一个(s-+1)维子空间中变化。 一般的,x在C"的(n-1)维子空间V中变动时, minR()s入, mxR()≥ XEVn-1 XEV-I 即,对于不同的V,R()的最小值及最大值有可能不同,其中各个 10
定理 1.设L span x , x , , x = { r r1 s + } (λ ≤λ ≤ ≤λ r r1+ s ) ,则 ( ) r x 0 x L minR x ≠ ∈ = λ ( ) s x 0 x L max R x ≠ ∈ = λ 这一结果不便于应用,希望对上述结果进行改造,改造成不依赖 于 i x 的一种表达方式。 1 a 0 = 和 n a 0 = 的情况均对应于 x 在(n-1)维的子空间内变动,x 在 L 中变动是在一个(s-r+1)维子空间中变化。 一般的,x 在 n C 的(n-1)维子空间Vn 1− 中变动时, ( ) n 1 2 x 0 x V min R x − ≠ ∈ ≤ λ ( ) n 1 n 1 x 0 x V max R x − − ≠ ∈ ≥ λ 即,对于不同的Vn 1− ,R x( )的最小值及最大值有可能不同,其中各个 10