
第二十讲矩阵特征值估计
第二十讲 矩阵特征值估计 1

特征值计算较困难,希望找到简便的特征值界限或分布范围的估 计方法。 一、特征值界的估计 定理1.设A∈R”,入为A的任意特征值,则有 im 其中,M=max ay-an I<i,j<n 2 证明:设x为A的属于特征值几的单位特征向量,即Ax=x,xHx=1, 则 2
特征值计算较困难,希望找到简便的特征值界限或分布范围的估 计方法。 一、 特征值界的估计 定理 1. 设 n n A R × ∈ ,λ为 A 的任意特征值,则有 ( ) ( 1) Im 2 n n λ M − ≤ 其中, 1 i,j n max 2 ij ji a a M ≤ ≤ − = 证明:设 x 为 A 的属于特征值λ的单位特征向量,即 Ax x = λ , 1 H x x = , 则 2
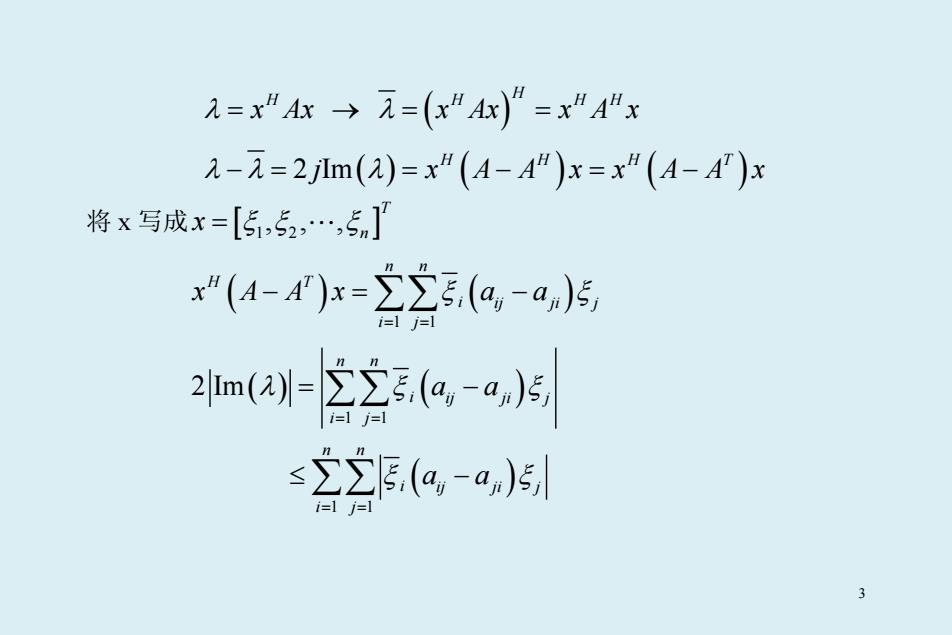
=x”A→元=(x”A)=x”Ax -元=2lm(2)=x”(A-A)x=x“(A-A)x 将x写成x=[5,52,…,5n] x(4-4)x=∑∑,(a,-a)5 2m(2-2空a,-a,片 ≤2∑E.(a,-a)5 3
H λ = x Ax → ( ) H H H H λ = = x Ax x A x 2 Im( ) ( ) ( ) H HH T λλ λ −= = − = − j x AA xx AAx 将 x 写成 [ 1 2 ,,, ] T n x = ξξ ξ ( ) ( ) 1 1 n n H T i ij ji j i j x AAx a a ξ ξ = = −= − ∑∑ ( ) ( ) ( ) 1 1 1 1 2 Im n n i ij ji j i j n n i ij ji j i j a a a a λξ ξ ξ ξ = = = = = − ≤ − ∑∑ ∑∑ 3
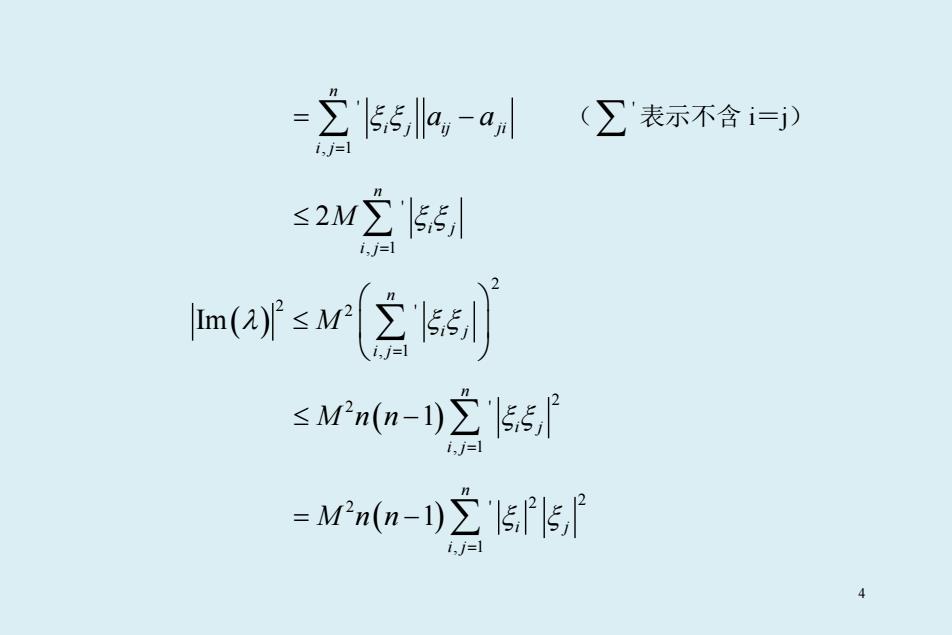
=∑5,-a(∑表示不含=D s2w空5 m(afsr含15 ≤Mn(n-)∑'ls5f =M2n(n-)∑'l515,f 4
' , 1 n i j ij ji i j ξ ξ a a = = ∑ − ( ' ∑ 表示不含 i=j) ' , 1 2 n i j i j M ξ ξ = ≤ ∑ ( ) 2 2 2 ' , 1 Im n i j i j λ M ξ ξ = ≤ ∑ ( ) 2 2 ' , 1 1 n i j i j Mnn ξ ξ = ≤ − ∑ ( ) 2 2 2 ' , 1 1 n i j i j Mnn ξ ξ = = − ∑ 4
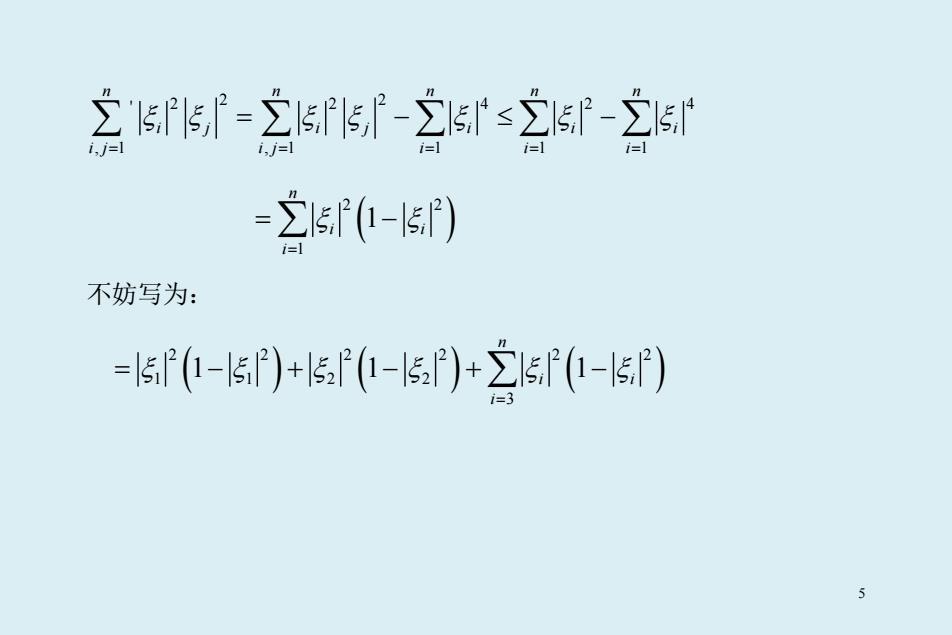
之5f-2f-sf-立 =-) 不妨写为: =(-5)+5a(-)+(-)
2 2 424 2 2 ' , 1 , 1 1 1 1 n n nnn ij ij i i i i j i j i i i ξξ ξξ ξ ξ ξ = = = = = ∑ ∑ ∑∑∑ = −≤− ( ) 2 2 1 1 n i i i ξ ξ = = − ∑ 不妨写为: ( ) ( ) ( ) 2 22 2 2 2 1 12 2 3 11 1 n i i i ξ ξξ ξ ξ ξ = = −+ −+ − ∑ 5

s- 1 ≤ 2 取等号的条件为5=5=7但=1,所以其它=0 a(0)s,9可 定理2.设A∈R”,1为A的任意特征值,则有 6
( ) ( ) ( ) 2 2 22 2 2 11 2 2 2 2 3 1 1 1 2 2 n i i i ξξ ξξ ξ ξ = + − + − ≤ + +− ∑ 1 2 ≤ 取等号的条件为 2 2 1 2 1 2 ξ ξ = = ,但 2 x =1,所以其它 2 0 i ξ = ∴ ( ) ( 1) Im 2 n n λ M − ≤ 定理 2. 设 n n A R × ∈ ,λ为 A 的任意特征值,则有 6

np Re()sr im(2)sns 其中,p=xh,t=mx4,+a,s=mxl,-a 二、盖尔圆法 定义:设A=(a,)meC",由方程z-a≤R=∑a,所确定的圆称 i法 为A的第i个盖尔圆,R称为盖尔圆的半径。 定理3:矩阵A的所有特征值均落在它的所有盖尔圆的并集之中。 证明:设A=(a)xn∈C”,1为A的某一个特征值,x为相应的特征 7
λ ρ ≤ n ( ) 1 Re 2 λ τ ≤ n ( ) 1 Im 2 λ ≤ ns 其中, 1 i,j n max ij ρ a ≤ ≤ = , 1 i,j n max ij ji τ a a ≤ ≤ = + , 1 i,j n max ij ji s aa ≤ ≤ = − 二、 盖尔圆法 定义:设 ( ) n n ij n n Aa C × × = ∈ ,由方程 1 n ii i ij j i j za R a = ≠ − ≤= ∑ 所确定的圆称 为 A 的第 i 个盖尔圆,Ri称为盖尔圆的半径。 定理 3:矩阵 A 的所有特征值均落在它的所有盖尔圆的并集之中。 证明:设 ( ) n n ij n n Aa C × × = ∈ ,λ为 A 的某一个特征值,x 为相应的特征 7

向量,将x写成x=[5,52,,5],设5。=max5 由Ax=x,考虑,行 ∑a5,=5。 (2-a6)5=∑a5,(0≠) a-立,风 对于A的特征值九,一定存在,(1≤≤n),使九落在A的第。个盖尔 8
向量,将 x 写成 [ 1 2 ,,, ] T n x = ξξ ξ ,设 0 i max i ξ ξ = 由 Ax x = λ ,考虑 0 i 行 0 0 1 n ij j i j a ξ λξ = ∑ = ( ) 00 0 0 ' 1 n ii i i j j j λξ ξ a a = − = ∑ ( ) 0 j i ≠ 0 0 0 0 0 0 0 ' ' 1 1 n n j j i i i j i j i j j i i aa aR ξ ξ λ = ξ ξ = −= ≤ ≤ ∑ ∑ 对于 A 的特征值λ,一定存在 0 i ( ) 0 1≤ ≤ i n ,使λ落在 A 的第 0 i 个盖尔 8

圆中,对于每个特征值都有相同的结论。 定理4.将矩阵A的全体盖尔圆的并集按连通部分分成若干个子集,(一 个子集由完全连通的盖尔圆组成,不同子集没有相连通的部分),对每 个子集,若它恰好由K个盖尔圆组成,则该子集中恰好包含A的K个 特征值。 说明:盖尔圆相互重叠时重复计算,特征值相重时也重复计算 a 证明:设A= ∈Cnxn 9
圆中,对于每个特征值都有相同的结论。 定理4. 将矩阵A 的全体盖尔圆的并集按连通部分分成若干个子集,(一 个子集由完全连通的盖尔圆组成,不同子集没有相连通的部分),对每 个子集,若它恰好由 K 个盖尔圆组成,则该子集中恰好包含 A 的 K 个 特征值。 说明:盖尔圆相互重叠时重复计算,特征值相重时也重复计算 证明:设 11 1 1 n n n n nn a a A C a a × = ∈ , 9

ua2 ua 3 u021 d22 u023 令B(u)= u031 ua32 033 1u03n uam uan2 uan3 0≤u≤l,B(0)=diag[a1a2…anm],B(=A B()的特征多项式是u的多项式,其特征值是u的连续函数,观 察u(0≤u≤1)变化的过程中B(u)特征值的变化,特征值只能在盖 尔圆连通的子集内变动,而不能跨出连通子集。 由此可见,由K个盖尔圆组成的连通子集恰好包含K个特征值。 10
令 ( ) 11 12 13 1 21 22 23 2 31 32 33 3 123 n n n n n n nn a ua ua ua ua a ua ua B u ua ua a ua ua ua ua a = 0 1 ≤ ≤ u ,B diag a a a (0) = [ 11 22 nn ],B A (1) = B u( )的特征多项式是 u 的多项式,其特征值是 u 的连续函数,观 察 u(0 1 ≤ ≤ u )变化的过程中B u( )特征值的变化,特征值只能在盖 尔圆连通的子集内变动,而不能跨出连通子集。 由此可见,由 K 个盖尔圆组成的连通子集恰好包含 K 个特征值。 10