
第八讲矩阵函数的求法
第八讲 矩阵函数的求法 1

一、利用Jordan标准形求矩阵函数。 对于矩阵的多项式,我们曾导出f(A)=Pf(J)P,f:多项式 f() f(J2) f(J)= f(Js) 21 实际上,以上结果不仅对矩阵的多项式成立,对矩阵的幂级数也成 2
一、利用 Jordan 标准形求矩阵函数。 对于矩阵的多项式,我们曾导出 1 f A Pf J P () () − = , f :多项式 ( ) 1 ( ) 2 ( ) ( ) f J f J f J f Js = ( ) 1 1 ( 1) () () ( ) ( ) ( ) 2! 1 ! i i i i i i i m f f f f f J m − ′ ′′ = − λ λ λ λ 实际上,以上结果不仅对矩阵的多项式成立,对矩阵的幂级数也成 2

立。由此引出矩阵函数的另一种定义及计算方法。 1.定义:设n阶矩阵A的Jordan标准形为J J小 1 0 2 1 J= ,J(2)= 1 Js」 且有非奇异矩阵P使得:PAP=J 对于函数f(z),若下列函数 f(2),f'(2),…,fm-(2) (九=1,2,…,S) 均有意义,则称矩阵函数f(A)有意义,且 3
立。由此引出矩阵函数的另一种定义及计算方法。 1. 定义:设n阶矩阵 A的 Jordan 标准形为J 1 2 J J J Js = , 1 0 1 ( ) 1 0 i i i i i J = λ λ λ λ λ 且有非奇异矩阵P使得: 1 P AP J − = 对于函数 f z( ),若下列函数 ( 1) ( ), ( ), , ( ) mi ii i ff f − λλ λ ′ ( 1,2, , ) λ = s 均有意义,则称矩阵函数 f A( )有意义,且 3

f() f(J2) f(A)=Pf(J)P-=P P-I f(Js) 。 m xm 2.矩阵函数的求法(步骤): I°求出A的Jordan标准形及变换矩阵P,P-AP=J 2°对于J的各Jordan块J,求出f(J),即计算出 4
( ) 1 ( ) 2 1 1 () () ( ) f J f J f A Pf J P P P f Js − − = = ( ) 1 1 ( 1) () () ( ) ( ) ( ) 2! 1 ! i i i i i i i i i m f f f f f m m m J − ′ ′′ = − × λ λ λ λ 2. 矩阵函数的求法(步骤): 1 求出 A的 Jordan 标准形及变换矩阵P, 1 P AP J − = 2 对于J 的各 Jordan 块 i J 求出 ( )i f J ,即计算出 4

f2),f'(2),,fm-(2) 并按照顺序构成f(J), an2G"a m.xm f() f(J2) 3°合成fJ)= f(Js)」 4°矩阵乘积给出f(A)=Pf(J)P- 5
( 1) ( ), ( ),......., ( ) mi i i i ff f − λλ λ ′ 并按照顺序构成 ( )i f J , ( ) 1 1 ( 1) () () ( ) ( ) ( ) 2! 1 ! i i i i i i i i i m f f f f f m m m J − ′ ′′ = − × λ λ λ λ 3 合成 ( ) 1 ( ) 2 ( ) ( ) f J f J f J f Js = 4 矩阵乘积给出 1 f A Pf J P () () − = 5

需要说明的是,计算结果与Jordan标准形中Jordan块的顺序无关。 1234 123 例1(教材P70例1.27).A= 求VA 12 1 [解]1°求出J及P 1100 [84 0 0 [2 -2 -1 0 110 4 -1 1 1 42 0 J= ,P= 11 2 -2 16 816 1 1 16 6
需要说明的是,计算结果与 Jordan 标准形中 Jordan 块的顺序无关。 例 1 (教材 P70 例 1.27). 1234 123 1 2 1 A = ,求 A [解] 1o 求出J 及P 1 1100 84 0 0 2 2 1 0 110 4 1 1 1 4 2 0 , , 1 1 2 2 16 8 16 1 1 16 JP P− − − − = = = − 6
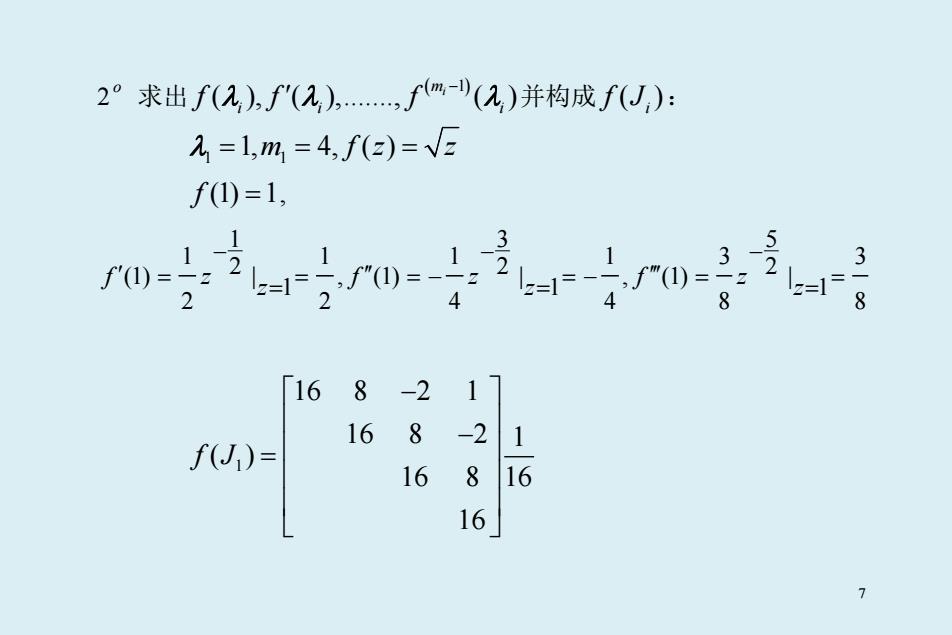
2°求出f(2),f'(2),,fm-少(元)并构成fJ): =1,m,=4,f(2)=V2 f(1)=1, -0--nm f0= 3 2=19 8 168 -2 1 16 8 -2 16 8 6 16 7
2o 求出 ( 1) ( ), ( ),......., ( ) mi i i i ff f − λλ λ ′ 并构成 ( )i f J : 1 1 λ = = = 1, 4, ( ) m fz z f (1) 1 = , 135 1 1 1 13 3 222 (1) | , (1) | , (1) | 111 2 2 4 48 8 fz f z f z zzz −−− ′ = = =− =− = = ′′ ′′′ = = = 1 16 8 2 1 16 8 2 1 ( ) 16 8 16 16 f J − − = 7

3°合成f(J)=f(J) 1111 111 4°求f(A)=Pf(J)P,f(A)= 11 1 说明: (1)f(2)=√E,在z=0不存在泰勒展开(而存在洛朗展开),如按原先 的幂级数定义,则根本无从谈f(A)的计算,可见新的定义延拓了原 来的定义; 8
3o 合成 1 fJ fJ () ( ) = 4o 求 1 f A Pf J P () () − = , 1111 111 ( ) 1 1 1 f A = 说明: (1) fz z ( ) = ,在z = 0不存在泰勒展开(而存在洛朗展开),如按原先 的幂级数定义,则根本无从谈 f A( )的计算,可见新的定义延拓了原 来的定义; 8

1 1 172 [12 3 47 111 1 2 3 (2)[f(A)] = 三 =A, 1 1 1 2 1 1 可见这样的√A确与A构成反函数: (3)矩阵函数的种类不仅是我们介绍的这种,如辛矩阵。以 4-[9]创,以我和这军的定文,a-甘9]1 B- 9
(2) 2 2 1111 1234 111 1 23 [ ( )] 11 1 2 1 1 f A A = = = , 可见这样的 A确与 2 A 构成反函数; (3)矩阵函数的种类不仅是我们介绍的这种,如辛矩阵。以 1 0 0 1 A − = − 为例,以我们这里的定义, 0 0 i A i ± = ± , 但 0 1 1 0 B − = 9

亦满足B=A,即B也可以看作某种√A 二、待定系数法求解矩阵函数 利用Jordan标准形求解矩阵函数的方法比较复杂,它需要求J 和P。下面我们介绍根据零化多项式求解矩阵函数的一种方法。 定律:n阶方阵A的最小多项式等于它的特征矩阵的第n个(也就是最 后一个)不变因子d,(2)。(可参见张远达《线性代数原理》 P215) 设n阶方阵A的不变因子反向依次为dn(2),dn(2),…,d(2),由 它们给出的初等因子分别为 (2-2)m,(2-元2)m,…,(2-入)m 10
亦满足 2 B A = ,即 B 也可以看作某种 A 二、待定系数法求解矩阵函数. 利用 Jordan 标准形求解矩阵函数的方法比较复杂,它需要求J 和P。下面我们介绍根据零化多项式求解矩阵函数的一种方法。 定律:n阶方阵 A的最小多项式等于它的特征矩阵的第n个(也就是最 后一个)不变因子 ( ) n d λ 。(可参见张远达《线性代数原理》 P215) 设n阶方阵 A的不变因子反向依次为 ( ), n d λ 1 1 ( ), , ( ) n d d − λ λ ,由 它们给出的初等因子分别为 1 2 1 2 ( ) ,( ) , ,( ) mm mr λλ λλ λλ −− − r ; 10