
第十讲矩阵的三角分解
第十讲 矩阵的三角分解 1

一、Gauss消元法的矩阵形式 n元线性方程组 a15+a1252+…+a1n5n=b a2151+a2252+…+a2n5n=b2 →Ax=b an5+an252+…+an5n=b /A=(a) x=[5,52,…5] b=[b,b2…bn]T 设A0=A=(ay)nm设A的k阶顺序主子式为△,若△,=a0≠0, 2
一、 Gauss 消元法的矩阵形式 n 元线性方程组 11 1 12 2 1 1 21 1 22 2 2 2 11 2 2 n n n n n n nn n n aa a b aa a b aa a b + ++ = + ++ = + ++ = ξξ ξ ξξ ξ ξξ ξ → Ax b = T 1 2 T 1 2 ( ) [, , ] [, ] ij n n A a x b bb b = = = ξξ ξ 设 ( ) (0) ij n n A Aa × = = ,设 A 的 k 阶顺序主子式为∆k,若 (0) 1 11 ∆= ≠ a 0, 2
可以令c1 a哥 并构造Frobenius矩阵 1 0 07 L= C211 -C21 1 0 】 xn -Cn 计算可得 3
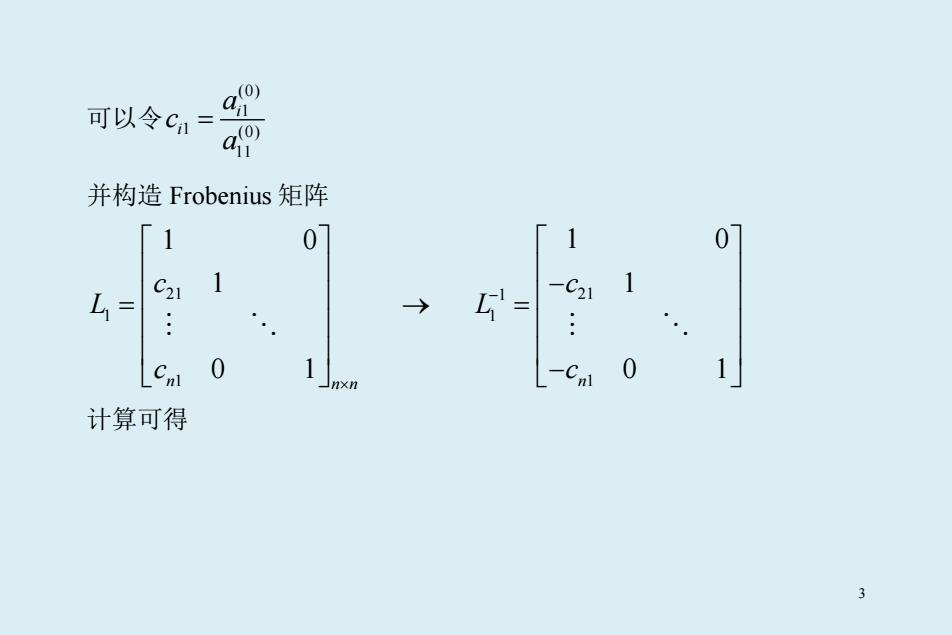
可以令 (0) 1 1 (0) 11 i i a c a = 并构造 Frobenius 矩阵 21 1 1 1 0 1 0 1 n n n c L c × = → 1 21 1 1 1 0 1 0 1 n c L c − − = − 计算可得 3

a A0=LA0)= a →A0=LAD 0 a 初等变换不改变行列式,故△2=a9a,若△,≠0,则a≠0,又可 定义 c2=a2(i=3,4,…m),并构造Frobenius矩阵 4
(0) (0) (0) 11 12 1 (1) (1) (1) 1 (0) 22 2 1 (1) (1) 2 0 n n n nn aa a a a A LA a a − = = → (0) (1) A LA = 1 初等变换不改变行列式,故 (0) (1) 2 11 22 ∆ = a a ,若 2 ∆ ≠ 0,则 (1) 22 a ≠ 0,又可 定义 (1) 2 2 (1) 22 ( 3,4, ) i i a cin a = = ,并构造 Frobenius 矩阵 4

Γ1 1 L2 C32 → -C32 C 1 一Cn2 1」 d a 是 A2)=L5A0= A0=LA2) 依此类推,进行到第(-1)步,则可得到 5
2 32 2 1 1 1 n L c c = → 1 2 32 2 1 1 1 n L c c − = − − (0) (0) (0) (0) 11 12 13 1 (1) (1) (1) 22 23 2 (2) 1 (1) (2) (2) 2 33 3 (2) (2) 3 n n n n nn aaa a aa a A LA a a a a − = = → (1) (2) A LA = 2 依此类推,进行到第(r-1)步,则可得到 5

(0) (0) (0) (0) r A- a a a4ia g (r=2,3,…,n) r d) 则A的r阶顺序主子式△,=a9a…a,》a,若△,≠0,则an≠0 可定义c, 并构造Frobenius矩阵 6
(0) (0) (0) (0) 11 1 1 1 1 ( 2) ( 2) ( 2) ( 1) 11 1 1 ( 1) ( 1) ( 1) ( 1) rr n rr r r rr rr r n r r rr rn r r nr nn a aa a aa a A a a a a − −− − − −− − − − − − − = ( 2,3, , ) r n = 则 A 的 r 阶顺序主子式 (0) (1) ( 2) 1 11 22 1 1 r r r r r rr aa a a − − ∆ = − − ,若 0 ∆ ≠ r ,则 1 0 r rr a − ≠ 可定义 1 1 r ir ir r rr a c a − − = ,并构造 Frobenius 矩阵 6
1 1 1 L, → = C 1 -Cr+lr 1 : .: C 1」 -Cnr 1 7
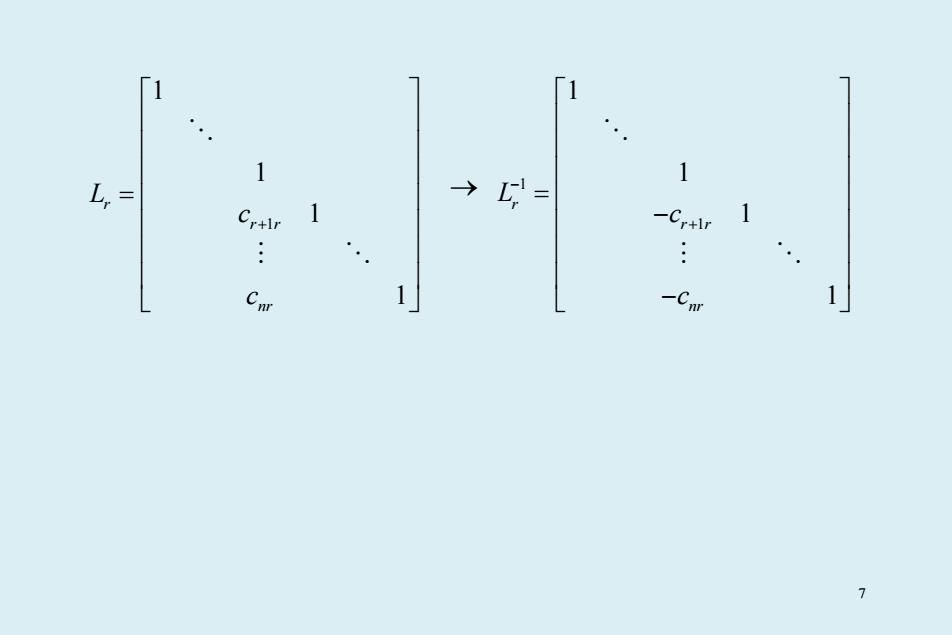
1 1 1 1 1 r r r nr L c c + = → 1 1 1 1 1 1 r r r nr L c c − + = − − 7
a a (0) (0) A()=L.A"-= q() r+1r+1 a) r+ln →A-)=L,A) (r=2,3,…,n-1) 直到第(n一1)步,得到 8
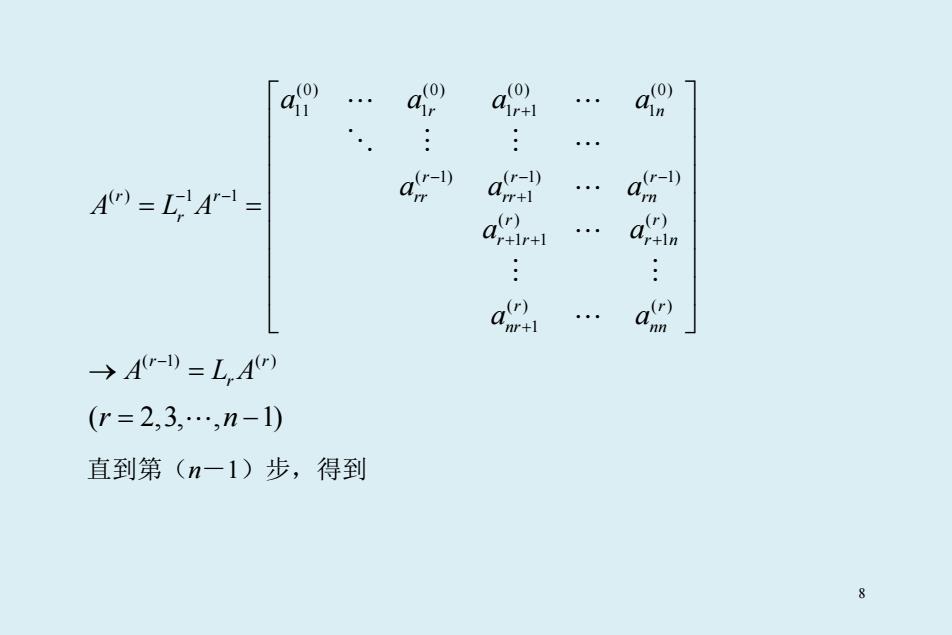
(0) (0) (0) (0) 11 1 1 1 1 ( 1) ( 1) ( 1) () 1 1 1 ( ) ( ) 1 1 1 ( ) ( ) 1 rr n rr r r r rr rr rn r r r r r r n r r nr nn a aa a aa a A LA a a a a + −− − − − + + + + + = = → ( 1) ( ) r r A LA r − = ( 2,3, , 1) r n = − 直到第(n-1)步,得到 8
(0) An-)= 则完成了消元的过程 而消元法能进行下去的条件是△≠0(r=1,2,…,n-1) 二、LU分解与LDU分解 A=A0=LA0=LL42=…=LLLg…Ln-1A- 容易求出 9
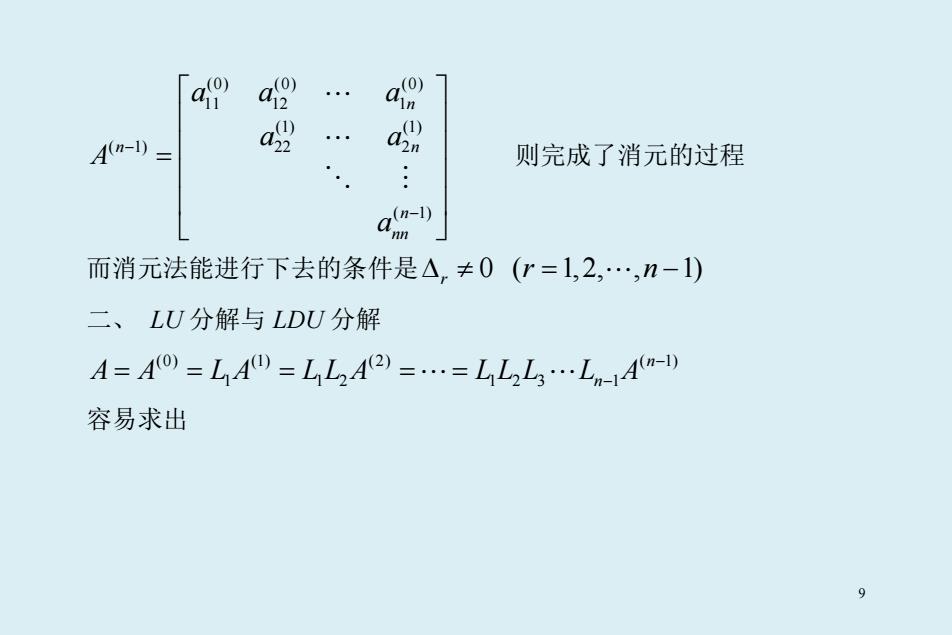
(0) (0) (0) 11 12 1 (1) (1) ( 1) 22 2 ( 1) n n n n nn aa a a a A a − − = 则完成了消元的过程 而消元法能进行下去的条件是 0 ∆ ≠ r ( 1,2, , 1) r n = − 二、 LU 分解与 LDU 分解 (0) (1) (2) ( 1) 1 12 123 1 n A A LA LL A LLL L A n − = = = = = − 容易求出 9

C21 1 L=LL2…Ln-= 为下三角矩阵 Cn-11 Cn-12 1 Cnl Cn2 Cnn-1 令U=A-)为上三角矩阵,则 A=LU (L:lower U:upper L:left R:right) 以上将A分解成一个单位下三角矩阵与上三角矩阵的乘积,就称 为LU分解或LR分解。 LU分解不唯一,显然,令D为对角元素不为零的n阶对角阵,则 10
21 12 1 11 12 12 1 1 1 1 1 n n n n n nn c L LL L c c cc c − − − − = = 为下三角矩阵 令 ( 1) n U A − = 为上三角矩阵,则 A LU = (L: lower U: upper L: left R: right) 以上将 A 分解成一个单位下三角矩阵与上三角矩阵的乘积,就称 为 LU 分解或 LR 分解。 LU 分解不唯一,显然,令 D 为对角元素不为零的 n 阶对角阵,则 10