
第27卷第1期 环境科 学 Vol,27,No.I 2006年1月 ENVIRONMENTAL SCIENCE Jan.,2006 基于MCMC法的水质模型参数不确定性研究 王建平,程声通,贾海峰“ (清华大学环境科学与工程系,北京100084) 箱要:参数识别是数学模型应用的前提,鉴于常用贝叶斯离散化方法在搜索复杂模型参数后验分布时的计算限制的原因,本 文引入了MCMC采样法.为考察MCMC法对参数后验分布的搜索性能和效率,进行了2个案例研究.结果表明,MCMC法对 参数后脸分布的搜索,无论是搜案性能还是搜索效率,均表现出了独特的优越性.同时,Gelman收敛判别准则计算表明, MCMC采样序列均能稳定收数到参数的后验分布上.可见,MMC法适用于复杂环境模型的参数识别和不确定分析研究, 关键词:马尔科大链蒙特卡罗法;水质膜型;不确定分析:参数识别 中图分类号:X192文献标识码:A文章编号:02503301(2006)01-0024-07 Markov Chain Monte Carlo Scheme for Parameter Uncertainty Analysis in Water Quality Model WANG Jian-ping,CHENG Sheng-tong,JIA Hai-feng Department of Environmental Science and Engineering,Tsinghua University,Beijing 100084,China) Abstract:Parameter identification plays an important role in environmental model application.Markoy Chain Monte Carlo method was introduced to estimate parameter uncertainty,since usual Bayes discrete methods were nol applicable to produce posterior distribution of complicated environmental model duc to the limit of computation.In order to study the performance and efficiency of MCMC,two case studics werc used.Results indicate that,either sampling performance or sampling efficiency.MCMC method both has its special advantages in producing posterior distribution.Moreover,results of Gelman convergence diagnostics indicate that sampling sequence can converge to stationary distribution.A key finding was that the MCMC scheme presented herein provided a powerful means of parameter identification and uncertainty analysis. Key words:MCMC;water quality model;uncertainty analysis;parameter identification 一个能反映客观实际的数学模型,只有在它得性是前1种参数识别思路的前提.然而,水质模型参 到合理的参数数值之后,才具有生命力山,随着水 数识别属于复杂非线性问题,参数响应曲面存在很 质模型在环境规划与管理中不断深人和广“泛地应 多凹谷和平坦区域,有大量局部极小点,优化算法往 用,模型结构复杂性急剧增长,模型参数在高维空间 往只能得到局部最优解,参数越多,参数响应曲面的 表现出了复杂的相关性结构和低灵敏度特征,从而 非线性度越高6},参数不可识别性问题越严重.科 直接导致了优化后验参数的识别问题2引.传统参 学家们采用各种方法克服模型的不可识别性问题, 数识别中仪局限于参数优化算法效率和精度等方面 最常见的方法是将模型的部分参数(通常是那些灵 的研究已经不能满足理论与实践的需要,相对于观 敏度较低的参数)预先采用先验知识固定,从而诚少 测数据和模型参数而言,基于现有科学认知体系构 待识别参数个数;或者对模型进行简化,去除那些不 建的模型结构是建模过程中不确定性的根本来 能被观测数据识别的子过程}.这种参数识别思路 源[4,然而由于缺乏深人研究结构不确定性的理论 的弊端是显而易见的.简化模型意味着棋型机理的 基础和有效技术手段,模型结构往往只能通过识别 诚少,这往往是研究人员不希望看到的,Reichert指 参数后验分布统计规律间接地得到验证,因而参数 出,一个唯一确定的模型用于预测,模型结构的简化 不确定性分析研究就显得格外重要, 可能导致模型预测不确定性的低估,尤其是当一个 过程在识别阶段不重要,而在预测阶段变得重要时 1参数不确定性分析 更是如此) 伴随着模型的发展和研究人员对模型结构特征 为了克服和解决参数不可识别的问题,基于贝 的认识,参数识别研究基本围绕2种思路展开引: 收稿日期:20041020:修订日期:2004-12-14 基金项目:国家自然科学林金资助项目(50209007) ①基于优化思想的参数识别思路,即传统的参数识 作者简介:王建平(1977一),男,博士研究生,上要从事环境系统分析 别思路;②基于不确定分析的参数识别思路.可识别 的理论与应用研究,E-mail:wangjp网tsinghua.org.cn 近讯联系人,jhf@tsinghua.edo.cn 万方数据
第27卷第1期 2006年1月 环 境 科 学 ENVIRoNMENTAL SCIENCE Vol 27.No I Jan,2006 基于MCMC法的水质模型参数不确定性研究 王建甲,程声通,贾海峰+ (清华大学环境科学与工程系.北京100084) 摘要:参数识别是数学模型应用的前提鉴于常用毋叶斯离散化方法在搜索复杂模型参数后验分布时的计算限制的原因,本 文引人了MCMC采样法为考察MCMC法对参数后验分布的搜索性能和效率,进行了2个案例研究结果表明.MCMC法对 参数后验分布的搜索,无论足搜索性能还是搜索效率,均表现出了独特的优越性同时,Gelman收敛判别准则计算表明. MCMC采样序列均能稳定收敛到参数的后验分布上可见,M('MC法适用于复杂环境模型的参数识别和小确定分析研究 关键词:马尔科丈链蒙特卡罗法;水质模型;不确定分析;参数识别 中圈分类号:X192文献标识码:A文章编号:0250 3301(2006)()1 0024 07 Markov Chain Monte Carlo Scheme for Parameter Uncertainty Analysis in Water Quality Model WANG J Jan ping,CHENG Sheng—tong,JIA Hai—feng (Department of Environmental Science and Engineering,Tsinghua UniverNty,Bering 100084,China) Abstract:Parameter identification plays an important role in environmental model application Markov Chain Monte Carlo method was introduced to estimate parameter uncertainty,ince usual Bayes discrete methods were not applicable to produce pcysterior distribution of complicated environmental model due to the limit of computation In order to study the performance and efficiency of MCMC,two ffaNe studies were used Results indicate that,either sampling performance 0r sampling efficiency,MCMC method both has its special advantages in producing posterior distribution Moreover,results of Gelman convergence diagnostics indicate that sampling sec!nence can converge to a stationary distribution A key finding was that the MCMC scheme presented herein provided a powerful illealls of parameter identification and uncertainty analysis Key words:MCMC;writer quality model;uncertainty analysis;parameter identification 一个能反映客观实际的数学模型,只有在它得 到合理的参数数值之后,才具有生命力-1 o随着水 质模型在环境规划与管理中不断深人和广泛地应 用,模型结构复杂性急剧增长,模型参数在高维空间 表现出了复杂的相关性结构和低灵敏度特征,从而 直接导致了优化后验参数的识别问题20传统参 数识别中仪局限于参数优化算法效率和精度等方面 的研究已经不能满足理论与实践的需要,相对于观 测数据和模型参数而言,基于现有科学认知体系构 建的模型结构是建模过程中不确定性的根本来 源-4。然而由于缺乏深入研究结构不确定性的理沦 基础和有效技术手段,模型结构往往只能通过识别 参数后验分布统计规律间接地得到验证,因而参数 不确定性分析研究就显得格外重要 1参数不确定性分析 伴随着模型的发展和研究人员对模型结构特征 的认识,参数识别研究基本围绕2种思路展开sl: ①基于优化思想的参数识别思路,即传统的参数识 别思路;②基于不确定分析的参数识别思路可识别 性是前1种参数识别思路的前提.然而,水质模型参 数识别属于复杂非线性问题,参数响应曲面存在很 多凹谷和平坦区域,有大量局部极小点,优化算法往 往只能得到局部最优解.参数越多,参数响应曲面的 非线性度越高”j,参数不可识别性问题越严重科 学家们采用各种方法克服模型的不可识别性问题, 最常见的方法是将模型的部分参数(通常是那些灵 敏度较低的参数)预先采用先验知识固定,从而减少 待识别参数个数;或者对模型进行简化,去除那些小 能被观测数据识别的子过程o o这种参数识别思路 的弊端是显而易见的简化模型意味着模型机理的 减少,这往往是研究人员不希望看到的,Reichert指 出,一个唯一确定的模型用于预测,模型结构的简化 可能导致模型预测不确定性的低估,尤其是当一个 过程在识别阶段不重要,而在预测阶段变得重要时 更是如此【“. 为了克服和解决参数不町识别的问题,基于贝 收稿日期:2004【0 20;修订日期:2004 12 14 基金项目:国家自然科学基金资助项目(50209007) 作者简介:王建平(1977一),男,博士研究生.上要从事环境系统分析 的理论与应用研究,E—l:wanv.ip@tsinghua orR cn *通讯联系人,1hf@tsinghua edu cn 万方数据

1期 环境科 学 25 叶斯理论的不确定性参数识别思路应运而生 于这种方法的应用,使得随机模拟在很多领域的计 Tiwari最早将贝叶斯理论用于生态模型的参数识 算中,显示出巨大的优越性,相比Monte Carlo法, 别,随后Hornberger与Spear提出了RSA方 MCMC法可大大降低计算量1.本文将应用 法[9.1o:,Beven提出了GLUE方法6.与传统的参数 MCMC法进行模型参数的不确定性分析研究 识别思路相比,参数不可识别性对贝叶斯统计法来 2MCMC法 说不再是一个问题,因此对于具有不可积别参数的 模型,贝叶斯方法无疑是很好地选择5,11.在统计 自1907年苏联数学家Markov提出马尔科夫 推断中使用先验分布的方法就是贝叶斯方法,也就 链的概念以来,经过世界各国几代数学家的相继努 是说,是否使用先验分布是区分贝叶斯统计和非贝 力,目前马尔科夫链已成为内容十分丰富、理论上相 叶斯统计的标志,非贝叶斯理论在做统计推断时只 当完整的数学分支.马尔科夫链理论已成为强有力 依据2类信息,即模型结构信息和数据信息.而贝叶 的数学工具,广泛应用于物理、化学、生物、天文、地 斯统计除了依据以上2类信息,还要利用另一类信 质、气象、计算机、通信等众多领域5.马尔科夫链 息,即未知参数的分布信息.由于这类信息是在获得 有严格的数学定义,其直观意义可理解为:随机系统 实际观测数据以前就有的,因此一般称为先验信息 中下一个将要达到的状态,仅依赖于目前所处的状 (A Prior Information).贝叶斯统计要求这类信息能 态,而与以往所经历过的状态无关5] 以未知参数的统计分布来表示,这个概率分布就称 MCMC法用于模型参数不确性分析的研究是 为先验分布,根据贝叶斯理论,参数的先验分布、样 近年米才发展起来的一种方法.Smith于1993 本信息和后验分布具有如下的关系121: 年16:提出利用MCMC法获取参数的后验分布,随 p(61y)=Cy10)(0) 后Tierney(1994)t与Chib(1995)l81相继发表了 (1) p(y) MCMC法用于参数不确定性分析的理论研究成果 b(0y)是参数的后验分布密度,p()是参数 2.1采样算法 的先验分布密度,p(y8)体现了在现有的数据条件 常用的MCMC采样算法有:Metropolis 下参数的似然度信息,p(y)为比例常数 Hastings算法1]和自适应Metropolis算法i9] 贝叶斯方法模式简单,概率形式优美.然而,它 2.1.1 Metropolis-Hastings算法 的数值解法并非总是容易的、直接的.实际应用巾需 Metropolis-Hastings算法(简称M-H法)是基于 进行随机变量的离散化,如随机采样算法RSA法和 贝叶斯推理框架下描述参数不确定性的最早、最通 GLUE法均属这一类算法,基于随机采样的统计方 用的一类MCMC采样器.M-H算法获取参数后验 法,可以获得模型参数的后验分布,而不再是一组单 分布的各态历经(Ergodicity)和收敛特性在文献中 一的最优参数,在一定程度上避免了由于“最优”参 已有详细研究,并给出了算法收敛的几何条件20】 数失真而带来的决策风险.但是,由于参数的产生是 有关M-H法的描述详见参考文献[15,17].应用M 随机的,属于“盲”搜索,当参数较多时,要想获得具 H采样器的关键是确定参数的推荐分布(Proposal 有一定代表性的采样点数,就必须进行大量的采样, distribution)和参数相关性的处理.对于复杂模型来 计算量随参数的增多呈指数增长,总之,贝叶斯方法 说,参数先验信息较少,确定参数的希望区域(高概 用于参数识别的思想已得到不同领域研究工作者的 率密度区域)非常困难,参数推荐分布的选择会带来 广泛认可,但是由于其巨大的计算量,在实际中很难 很大的初始不确定性,导致收敛速率缓慢,为改进 推广应用,这些离散贝叶斯方法只适合参数个数较 MCMC采样器的搜索效率,人们希望算法随采样过 少的情况,Jorgensen指出,当参数个数超过3~5个 程自适应地调整参数的推荐分布,这样,自适应的 时,参数识别过程将非常耗时] Metropolis算法应运而生.自适应的Metropolis算法 离散贝叶斯方法应用的主要障碍出在计算上, 可以有效地解决MH法存在的问题 即使采用高性能计算机进行模拟,也面临着计算复 2.1.2自适应Metropolis算法 杂性的问题5,刀.20世纪90年代,研究人员将马尔 自适应Metropolis算法(Adaptive Metropolis, 科夫链蒙特卡罗法(Markoy Chain Monte Carlo, AM)是Haario在2001年提出的一种改进MCMC MCMC)14引入到参数不确定性研究中,用于待估 采样器1町,相比传统M-H算法,AM算法不再需要 参数的贝叶斯分布采样,以估计参数的后验分布.由 事先确定参数的推荐分布,而是由后验参数的协方 万方数据
l期 环 境 科 学 叶斯理论的不确定性参数识别思路应运而生 Tiwari最早将贝叶斯理论用于生态模型的参数识 别”J,随后Hornberger与Spear提出了RSA方 法。9’10一,Beven提出了GLUE方法№J.与传统的参数 识别思路相比,参数不可识别性对贝叶斯统计法来 说不再是一个问题,因此对于具有不可识别参数的 模型,贝叶斯方法无疑是很好地选择【5,111在统计 推断中使用先验分布的方法就是贝叶斯方法,也就 是说,是否使用先验分布是区分贝叶斯统计和非贝 叶斯统计的标志非贝叶斯理论在做统计推断时只 依据2类信息,即模型结构信息和数据信息,而贝叶 斯统计除了依据以上2类信息,还要利用另一类信 息,即未知参数的分布信息.由于这类信息是在获得 实际观测数据以前就有的,因此一般称为先验信息 (APrior Informafion).贝叶斯统计要求这类信息能 以未知参数的统计分布来表示,这个概率分布就称 为先验分布.根据贝叶斯理论,参数的先验分布、样 率信息和后验分布具有如下的关系一”J: 口(8 v):丛卫善2拿型 (1) pL■, P(0 y)是参数的后验分布密度,P(∞是参数 的先验分布密度,P(y∞体现了在现有的数据条件 下参数的似然度信息,P(y)为比俩常数 贝叶斯方法模式简单,概率形式优美.然而,它 的数值解法并非总是容易的、直接的.实际应用巾需 进行随机变量的离散化,如随机采样算法RSA法和 GLUE法均属这一类算法.基于随机采样的统计方 法,可以获得模型参数的后验分布,而不再是一组单 一的最优参数,在一定程度上避免了由于“最优”参 数失真而带来的决策风险但是,由于参数的产生是 随机的,属于“盲”搜索,当参数较多时,要想获得具 有一定代表性的采样点数,就必须进行大量的采样, 计算量随参数的增多呈指数增长.总之,贝叶斯方法 用于参数识别的思想已得到不同领域研究工作者的 广泛认町,但是由于其巨大的计算量,在实际中很难 推广应用,这些离散贝叶斯方法只适合参数个数较 少的情况,Jorgensen指出,当参数个数超过3~5个 时,参数识别过程将非常耗时Ll… 离散贝叶斯方法应用的主要障碍出在计算上, 即使采用高性能计算机进行模拟,也面临着计算复 杂性的问题。“20世纪90年代,研究人员将马尔 科夫链蒙特卡罗法(Markov Chain Monte Carlo, MCMC)[14引入到参数不确定性研究中,用于待估 参数的贝叶斯分布采样,以估计参数的后验分布由 于这种方法的应用,使得随机模拟在很多领域的计 算中,显示出巨大的优越性,相比Monte Carlo法, MCMC法可大大降低计算量[1“.本文将应用 MCMC法进行模型参数的不确定性分析研究. 2 MCMC法 自1907年苏联数学家Markov提出马尔科夫 链的概念以来,经过世界各国几代数学家的相继努 力,目前马尔科夫链已成为内容十分丰富、理论上相 当完整的数学分支马尔科夫链理论已成为强有力 的数学工具,广泛应用于物理、化学、生物、天文、地 质、气象、计算机、通信等众多领域【15 J.马尔科夫链 有严格的数学定义,其直观意义可理解为:随机系统 中下一个将要达到的状态,仅依赖于目前所处的状 态,而与以往所经历过的状态无关【i“. MCMC法用于模型参数不确性分析的研究是 近年米才发展起来的一种方法,Smith于1993 年.16j提出利用MCMC法获取参数的后验分布,随 后Tierney(1994)_7一与Chib(1995)【18相继发表了 MCMC法用于参数不确定性分析的理论研究成果 2.1 采样算法 常用的MCMC采样算法有:Metropolis Hastings算法Ⅲ‘o和自适应Metropolis算法…1 2.1.1 Metropolis—Hastings算法 Metropolis—Hastings算法(简称M—H法)是基于 贝叶斯推理框架下描述参数不确定性的最早、最通 用的一类MCMC采样器.M—H算法获取参数后验 分布的各态历经(Ergodicity)和收敛特性在文献中 已有详细研究,并给出了算法收敛的几何条件[20] 有关M—H法的描述详见参考文献[15,17].应用M— H采样器的关键是确定参数的推荐分布(Proposal distribution)和参数相关性的处理对于复杂模型来 说,参数先验信息较少,确定参数的希望区域(高概 率密度区域)非常困难,参数推荐分布的选择会带来 很大的初始不确定性,导致收敛速率缓慢为改进 MCMC采样器的搜索效率,人们希望算法随采样过 程自适应地调整参数的推荐分布,这样,自适应的 Metropolis算法应运而生.自适应的Metropolis算法 可以有效地解决M。H法存在的问题 2 1.2 自适应Metropolis算法 自适应Metropolis算法(Adaptive Metropolis, AM)是Haario在2001年提出的一种改进MCMC 采样器“…相比传统M H算法,AM算法不再需要 事先确定参数的推荐分布,而是由后验参数的协方 万方数据

26 环境科 学 27卷 差矩阵来估算.后验参数的协方差矩阵在每次迭 据参数的先验分布来确定 代后自适应地调整,这样,第1步参数的推荐分布为 e和Sd的确定.本研究中e=105,54= 均值:,协方差C:的多元正态分布.协方差计算公 (2.4)2/d,d为参数个数[91 式如式(2),在初始0次迭代中,协方差矩阵C:取 参数先验分布的确定,本研究采用均匀分布. 固定值(C4,之后自适应更新, 似然度函数的确定,似然度函数的确定有很多 Co 方法[6」,本研究似然度函数的形式为: C:= i么i0(2) sCov(0o,…,0,-l)+saela i≥i0 其中,e为一个较小的数,以确保C,不成为奇 p(y)= 1 (5) 异矩阵:5为个比例因子,依赖于参数的空间维 度d,以确保接受率在一个合适范围内;【4为d维 =1 单位矩阵.第i+1次选代,由公式(2)可推出协方差 21Ca-C41 计算公式(3),可以看到,计算量很小 其中,E4= C-+(通明:- 2c 式中,k一1,2,…,L:L为系统模拟的水质状态变 (i+1)0,0+0,8+ela) (3) 量数;i=1,2,…,n;n为监测次数;E为第k变 其中,日,-1和日:为前i-1和i次迭代参数的 量的相对误差;C:为第i次监测第k变量的浓度模 均值 拟值;C:为第i次监测第k变量的浓度观测值 AM算法的搜索流程如下: 2.2.2收敛判新准唰 (1)初始化,i=0: MCMC研究的一个重要任务是判断采样序列 (2)状态随机产生和接受; 是否收敛到参数后验分布,理论上,一个各向同性的 (a)利用公式(2)计算C: 采样器在t→∞时一定收敛,然而在实际应用中并 (b)产生推荐参数值日·一N(6:,C,); 非如此.Gelman21]在1992年提出了一种定量的收 (c)计算接受概率a; 敛诊断指标√R,称为比例缩小得分(Scale a min1, (y18·)(0·) (4) Reduction Score),计算方法如下: p(y18:)(0:) 参数物理意义同前 。+g (6) (d)产生随机数u-U[0,1]: 其中,g为每一参数采样序列的迭代次数;9为用于 (c)若u<a接受9,+1=8”,否则0:+1=0: 评价的序列数;B/g为g个序列的平均值的方差; (3)重复(a)~(e)直到产生足够的样本为止 W为q个序列的方差的平均值.计算每一参数的比 AM算法的最大优点是推荐分布随计算过程自 例缩小得分√R,若接近于1表示参数收敛到了后 动更新,不再需要事先指定.同时,相比传统M-H算 验分布上, 法,参数同时更新,不再需要分组更新,计算量大大 Gelman提出的方法为多序列对比方法,研究中 减少.基于以上优点,本研究将采用AM算法来搜 考察单序列是否稳定的方法有平均值法和方差法, 索参数后验分布 即考察迭代过程中的平均值和方差是否稳定,显然, 2.2MCMC法采样设计 单序列评价方法不能判别序列是否全局收敛 2.2.1算法参数选择 初始化阶段(“Burn in”period):受模型参数初 3案例研究 值0。影响的初始迭代序列9:,即0:后的采样点将 3.1双蜂概率密度函数(案例1) 收敛到参数的后验分布上.初始化阶段在统计分析 为考察MCMC法对参数后验分布的搜索效率 中必须去除,以消除初值的影响,初始化阶段长度的 和性能,本研究首先利用2.2节设计的算法对如下 确定是MCM(法应用的一个雅点.通常根据统计结 的双峰概率密度函数进行采样研究 果确定 参数初始协方差矩阵C。和初始送代次数i的 (9)=1 2exp[-2(29-8r] 确定,AM算法中C。的指定没有严格要求,通常根 (7) 万方数据
26 环 境 科 学 27卷 差矩阵来估算.后验参数的协方差矩阵在每一次迭 代后自适应地调整这样,第i步参数的推荐分布为 均值0:,协方差C.的多元正态分布协方差计算公 式如式(2),在初始io次迭代中,协方差矩阵C。取 固定值c。之后自适应更新. f:jc。 K io(2) 【sdCov(00,…~0 1)+5deId i≥io。 其中,e为一个较小的数,以确保c,不成为奇 异矩阵:劫为一个比例因子,依赖于参数的空间维 度d,以确保接受率在一个合适范围内;L为d维 单位矩阵.第i+1次迭代,由公式(2)可推出协方差 计算公式(3),可以看到,计算量很小 cⅢ=≮!c,+挚(io。%一 (i+1)口p?+0fl!+EL) (3) 其中,目:一】和自。为前i一1和i次选代参数的 均值 AM算法的搜索流程如下: (1)初始化,i=0; (2)状态随机产生和接受; (a)利用公式(2)计算C,; (b)产生推荐参数值0。~N(0,,c,); (c)计算接受概率a; 参数物理意义同前. a—n{-,瓷黼}㈤ (d)产生随机数“~u[o,1]; (e)若“<Ⅱ接受B+l=0+,否则d:+1=0。; (3)重复(a)~(c)直到产生足够的样本为止 AM算法的最大优点是推荐分布随计算过程自 动更新,不再需要事先指定同时,相比传统M—H算 法,参数同时更新,不再需要分组更新,计算量大大 减少.基于以上优点,本研究将采用AM算法来搜 索参数后验分布 2.2 MCMC法采样设计 2.2.1 算法参数选择 初始化阶段(“Burn in”period):受模型参数初 值0。影响的初始迭代序列0。,即0:后的采样点将 收敛到参数的后验分布上初始化阶段在统计分析 中必须去除,以消除初值的影响.初始化阶段长度的 确定足MCMC法应用的一个难点.通常根据统计结 果确定 参数初始协方差矩阵Co和初始迭代次数i。的 确定AM算法中c。的指定没有严格要求,通常根 据参数的先验分布来确定 e和跆的确定本研究中£=10 ,5d= (2.4)2/d,d为参数个数o”J 参数先验分布的确定.本研究采用均匀分布 似然度函数的确定似然度函数的确定有很多 方法.6 J,本研究似然度函数的形式为: p(Y I目)=12一 (5) Ⅱ最^=1 ∑I C。一o“I 其ep,E^=三L—-—一 ∑C。 i—I 式中,le一1,2,…,L;L为系统模拟的水质状态变 鼍数;卢l,2,…,”;n为监测次数;E^为第^变 量的相对误差;Ck,为第i次监测第^变量的浓度模 拟值;e;:为第i次监测第^变量的浓度观测值 2.2.2 收敛y-8断准则 MCMC研究的一个重要任务是判断采样序列 是否收敛到参数后验分布理论上,一个各向同性的 采样器在f—oo时一定收敛,然而在实际应用中并 非如此.Gelmankll在1992年提出了一种定量的收 敛诊断指标瓶,称为比例缩小得分(Scale Reduction Score),计算方法如下: 瓶=√哼+糍面B (6) 其中,g为每一参数采样序列的迭代次数;q为用于 评价的序列数;B/g为q个序列的平均值的方差; Ⅳ为口个序列的方差的平均值计算每一参数的比 例缩小得分~,R.若接近于1表示参数收敛到了后 验分布上 Gelman提出的方法为多序列对比方法,研究中 考察单序列是否稳定的方法有平均值法和方羞法, 即考察迭代过程中的平均值和方差是否稳定.显然, 单序列评价方法不能判别序列是否全局收敛 3案例研究 3.1 双峰概率密度函数(案例1) 为考察MCMC.法对参数后验分布的搜索效率 和性能,本研究首先利用2.2节设计的算法对如下 的双峰概率密度函数进行采样研究 删=去ex一卜丢卟去唧[_2*(20删2] (7) 万方数据

1期 环 培科学 27 该函数在6=0和8=4位置附近呈双峰特征 按式(6)计算√反=1.0001,说明参数样本收敛到了 3.2WASP模型应用(案例2) 后验分布 本案例以WASP模型系统在密云水库水质模 表1待识别水质模型参数 拟中的应用为例来探讨MCMC法用于搜索水质模 Table 1 Parameters necdod to identify in water yualily model 型参数后验分布及进行参数不确定分析的有效性和 参数名称 物理意义 参数范围 优越性.有关模型时空概化、输人配置等内容详见文 K12C 20℃条件下的硝化速度系数d1 0.05-0.35 K20C 20℃条件下的反硝化速度系数/d~1 0.01-0.2 献[22]. KIC 浮游植翻的饱和生长率1 1.5-4 WASP23]是由美国国家环保局开发的用于地 KIRC 20℃条件下浮游植物的内源呼吸速率日【0.05~0.2 表水水质模拟的模型,它提供了一个灵活的动态模 浮游植物内的碳比(峡省值为0.25) NCRB 0.2-0.3 拟系统.如图1所示,WASP可以模拟8个指标,分 ng"g】 浮游植物内的磷碳比(蚊省值为0.025) 别为:氨氮(NH)、硝酸盐氮(NO)、溶解性磷酸盐 PCRB 0.02-0.03 /mg'mg (OPOa)、叶绿素a(Chl-a)、碳生化需氧量(CBOD)、 KDC 20℃条件下的CBOD降解遂布/d【 0.01-0.1 溶解氧(DO)、有机氮(ON)和有机磷(OP).在 K2 20℃条件下,水体的复氧速度常数日t0.1-0.2 K71C 溶解有机氢的矿化速度· 0.01-0.1 wASP模型系统中水质模块EUTRO5的水质参数 K83C 溶解有机磷的矿化速度~· 0.01-0.1 有42个之多,通过灵敏度分析提取了灵敏度较高的 参数,结果如表1所示 1.0 0.8 06 0.4 ON 0.2 NH; 0 PHYT (以骤表示) C:N:P 图2双蟑橛率密度面数和MCMC法采样4000次的直方图 CHOD Fig.2 Bimodal probability distribution and histogram of OPO 40)00 samples generated using AM 00 6 4.2案例2 AM算法控制参数设置如下:参数始协方差 底泥 大气复氧 矩阵C。为对角矩阵,参数方差取参数搜索范围的 1/10,参数搜索范围见表1:初始迭代次数io= 图】水质模拟反应动力学关系 1000.利用AM算法搜索表1中参数的后验分布, Fig.I Wasp Eutrophication (EUTRO)state variables relationships 每次采样20000次,平行运行5次,初始化阶段为 10000次(确定依据见后面分析),这样5次平行试 验共采集了50000个样本用于参数后验分布的统计 4结果与讨论 分析 4.1案例1 4.2.1收敛性判断 AM算法配置为:参数初始协方差矩阵C。为对 采样序列是否已收敛到参数后验分布是后续研 角矩阵,取参数搜索范围的1/20,参数搜索范围为 究的基础.利用公式(6)计算的√R演化过程如图3 [-5,10j;初始迭代次数i。=100.算法平行运行5 所示,在搜紫初期,即迭代次数i5000后,√R联续缓慢下降并最终稳定到一 本,图2为参数后验分布的直方图,可以看出,式 个略大于1.0的数值上.各参数均呈现出这一规律, (7)中参数日的后验分布得到了很好地采样,同时 说明不同参数的MCMC采样序列均能稳定收敛到 万方数据
1期 环 境 科 学 该函数在0=0和0=4位置附近呈双峰特征. 3.2 WASP模型应用(案例2) 本案例以WASP模型系统在密云水库水质模 拟中的虚用为例来探讨MCMC法用于搜索水质模 型参数后验分布及进行参数不确定分析的有效性和 优越性有关模型时空概化、输人配置等内容详见文 献[22]. WASPK“是由美国国家环保局开发的用于地 表水水质模拟的模型,它提供了一个灵活的动态模 拟系统.如图1所示,wAsP可以模拟8个指标,分 别为:氨氮(NH3)、硝酸盐氮(N03)、溶解性磷酸盐 (oPq)、叶绿素a(Chl—a)、碳生化需氧量(CBOD)、 溶解氧(DO)、有机氮(ON)和有机磷(Op)在 WASP模型系统中水质模块EUTR05的水质参数 有42个之多,通过灵敏度分析提取了灵敏度较高的 参数,结果如表1所示 舶1水质模拟反应动力学关系 Fig I Wasp Eutrophication(EUTRO)state variable_s relationships 4结果与讨论 4.1 案例1 AM算法配置为:参数初始协方差矩阵c。为对 角矩阵,取参数搜索范围的1/20,参数搜索范嗣为 [5,10j;初始迭代次数i。=100.算法平行运行5 次,每次采集1 000个样本,摈弃前200个样本,以消 除初始化阶段的影响,这样5次运行共4 000个样 本,图2为参数后验分布的直方图,可以看出,式 (7)中参数0的后验分布得到了很好地采样,同时 按式(6)计算瓶=1.0001,说明参数样本收敛到了 后验分布 表1待识别水质模型参数 Table 1 P0-raraeters needed to identify in wa[er quailIY model 图2双嶂概率密度函数和MCMC法采样4 000次的直方图 Fig 2 BimMa{probability distribution and histogratia of 4 000 samples generated using AM 4.2 案例2 AM算法控制参数设置如下:参数初始协方差 矩阵c。为对角矩阵,参数方差取参数搜索范围的 l/10,参数搜索范围见表1;初始迭代次数in= 1000.利用AM算法搜索表1中参数的后验分布, 每次采样20 000次,平行运行5次,初始化阶段为 10 000次(确定依据见后面分析),这样5次平行试 验共采集了50 000个样本用于参数后验分布的统计 分析. 4.2.1 收敛性判断 采样序列是否已收敛到参数后验分布是后续研 究的基础.利用公式(6)计算的√R演化过程如图3 所示在搜索初期,即迭代次数i5000后,~/R继续缓慢下降并最终稳定到一 个略大于1.0的数值上.各参数均呈现出这一规律, 说明不同参数的MCMC采样序列均能稳定收敛到 万方数据
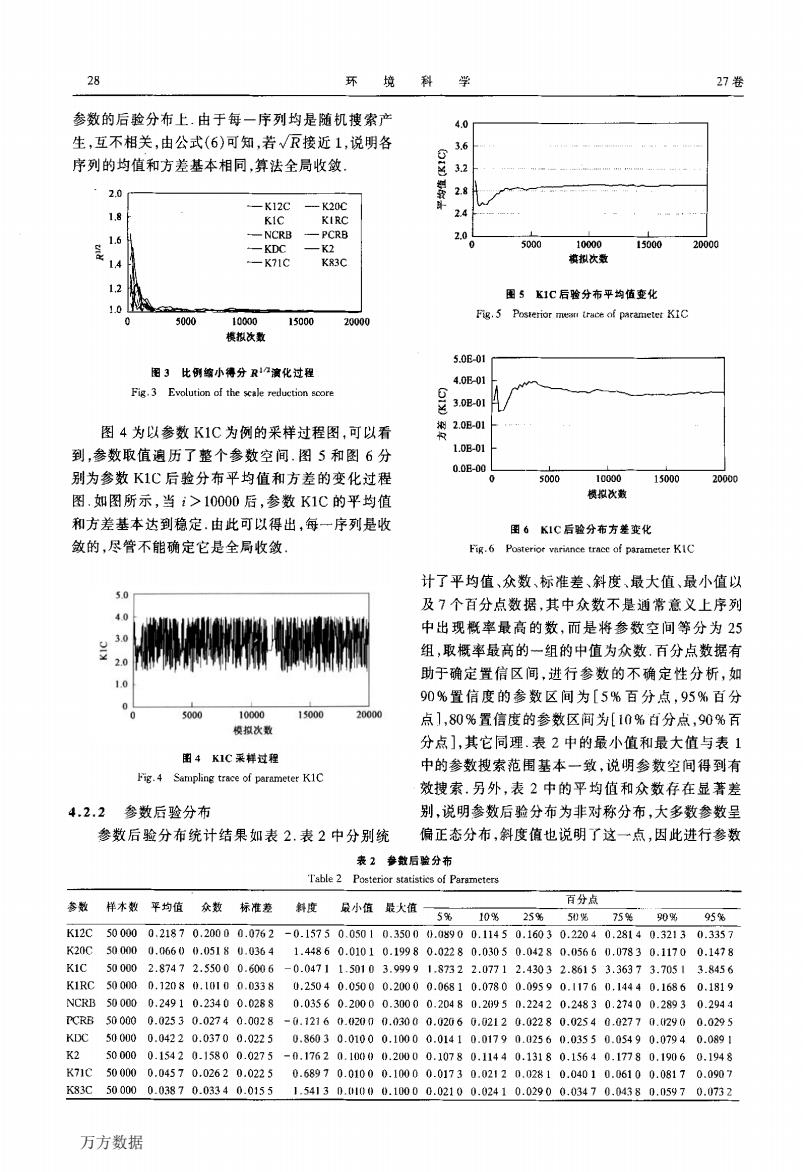
28 环 境 学 27卷 参数的后验分布上由于每一序列均是随机搜索产 0 生,互不相关,由公式(6)可知,若√R接近1,说明各 3.6 序列的均值和方差基本相同,算法全局收敛 2.0 28 仰 -K12C --K20℃ KIRC 24 KIC 16 -NCRB -PCRB 2.0 KDC K2 5000 、10000 15000 20000 14 K7IC K83C 祺拟次数 1.2 围5K1C后验分布平均值变化 Fig.5 Posterior mean trace of parametet KIC 0 5000 10000 15000 20000 模椒次数 5.0E-01 图3比例皱小得分R12演化过程 4.0E01 Fig.3 Evolution of the scale reduction soore 3.0E-01 图4为以参数K1C为例的采样过程图,可以看 掬2.0E-01 到,参数取值遍历了整个参数空间.图5和图6分 1.0E-01 0.0E-00 别为参数K1C后验分布平均值和方差的变化过程 0 5000 10000 15000 20000 图.如图所示,当i>10000后,参数K1C的平均值 模拟次数 和方差基本达到稳定,由此可以得出,每一序列是收 留6K1C后验分布方差变化 敛的,尽管不能确定它是全局收敛 Fig.6 Posterior variance trace of parameter KIC 计了平均值、众数、标准差、斜度、最大值、最小值以 5.0 及7个百分点数据,其中众数不是通常意义上序列 4.0 中出现概率最高的数,而是将参数空间等分为25 3.0 组,取概率最高的一组的中值为众数,百分点数据有 2.0 助于确定置信区间,进行参数的不确定性分析,如 1.0 90%置信度的参数区间为[5%百分点,95%百分 5000 10000 13000 20000 点1,80%置信度的参数区间为[10%百分点,90%百 模拟次数 分点],其它同理.表2中的最小值和最大值与表1 留4K1C采样过程 中的参数搜索范围基本一致,说明参数空间得到有 Fig.4 Sampling trace of parameter K1C 效搜索,另外,表2中的平均值和众数存在显著差 4.2.2参数后验分布 别,说明参数后验分布为非对称分布,大多数参数呈 参数后验分布统计结果如表2.表2中分别统 偏正态分布,斜度值也说明了这一点,因此进行参数 表2参数后验分布 'T'able 2 Posterior statistics of Parameters 态数 样木数平均值 众数标准差 百分点 斜度 最小值最大值5%10%25%50% 75g 0% 95第 K12C500000.21870.20000.0762-0.15750.05010.35000.0s900.11450.16030.22040.28140.32130.3357 K20C500000.06600.05180.03641.44860.01010.19980.02280.03050.04280.05660.07830.11700.1478 K1C500002.87472.55000.6006-0.04711.50103.99991.87322.07712.43032.86153.36373.70513.8456 K1RC500000.12080,10100.03380.25040.05000.20000.06810.07800.09590.11760.14440.16860.1819 NCRB500000.24910.23400.02880.03560.20000.30000.20480.2950.22420.24830.27400.28930.2944 TCRB500000.02530.02740.0028-0.12160.2000.03000.02060.02120.02280.0254002770.2900.0295 KD℃500000.04220.03700.02250.86030.01000.10000.01410.01790.02560.03550.05490.07940.0891 K2500000.15420.15800.0275-0.17620.10000.20000.10780.11440.13180.15640.17780.19060.1948 K71C500000.04570.02620.02250.68970.01000.10000.01730.02120.02810.04010.06100.08170.0907 K83C500000.03870.03340.01551.54130.01000.10000.02100.02410.02900.03470.04380.05970.0732 万方数据
环 境 科 学 27卷 参数的后验分布上由于每一序列均是随机搜索产 生,互不相关,由公式(6)可知,若~/百接近1,说明各 序列的均值和方差基本相同,算法全局收敛. 囤3 比例缩小得分置伸演化过程 Fig 3 Evolution of the scale reduction…e 图4为以参数K1c为例的采样过程图,可以看 到,参数取值遍历了整个参数空间图5和图6分 别为参数K1C后验分布平均值和方差的变化过程 图如图所示,当i>10000后,参数K1C的平均值 和方差基本达到稳定,由此可以得出,每一序列是收 敛的,尽管不能确定它是全局收敛 圈4 KIC采样过程 Fig 4 Sampling trace of parameter K1C 4。2。2 参数后验分布 参数后验分布统计结果如表2表2中分别统 。 邕 魁 轷 } 图s KIC后验分布平均值变化 Fig 5 Posterior n…“Ⅵce of parameter KtC 圈6 KIC后验分布方差变化 Fig 6 P嘣terior variance tracc of parameter K【C 计了平均值、众数、标准差、斜度、最大值、最小值以 及7个百分点数据,其中众数不是通常意义上序列 中出现概率最高的数,而是将参数空间等分为25 组,取概率最高的~组的中值为众数百分点数据有 助于确定置信区间,进行参数的不确定性分析,如 90%置信度的参数区问为[5%百分点,95%百分 点],80%置信度的参数区问为[10%日分点,90%百 分点],其它同理表2中的最小值和最大值与表1 中的参数搜索范围基本一致,说明参数空间得到有 效搜索.另外,表2中的平均值和众数存在显著差 别,说明参数后验分布为非对称分布,大多数参数呈 偏正态分布,斜度值也说明了这一点,因此进行参数 表2参数后验分布 Fable 2 Posterior statistics of Parameters 万方数据
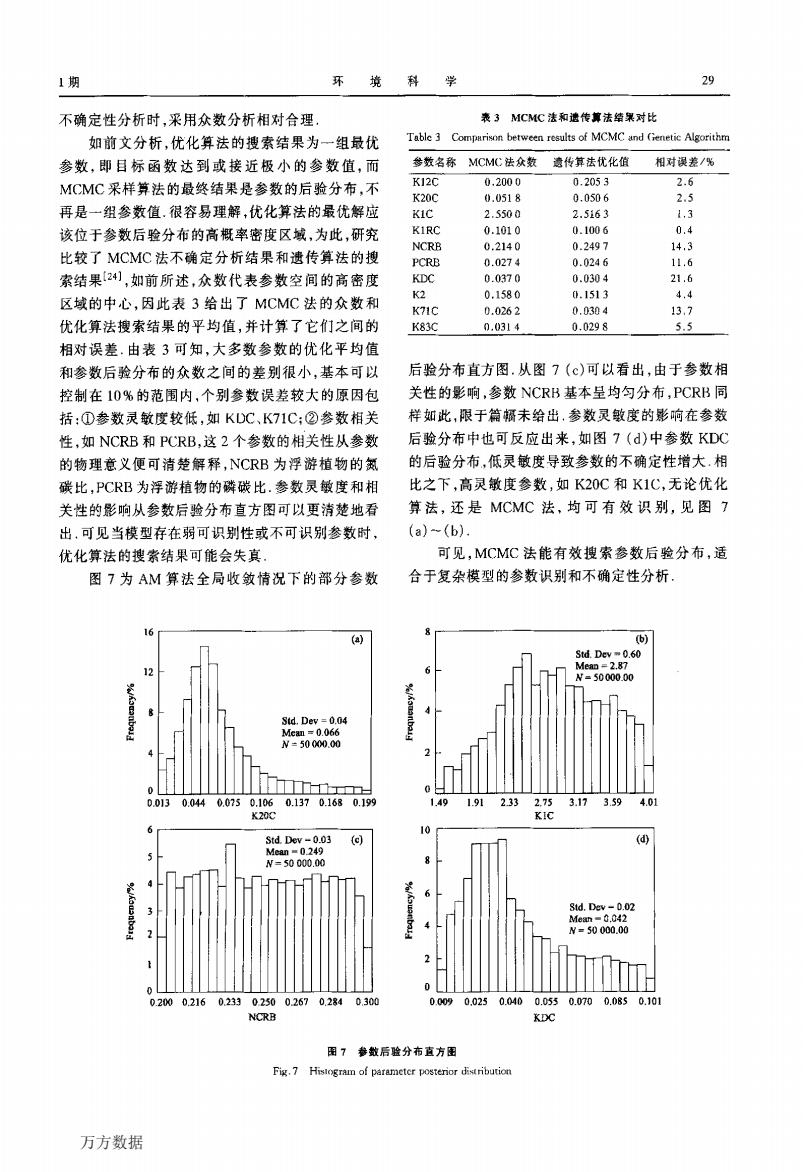
1期 环境 学 29 不确定性分析时,采用众数分析相对合理 表3MCMC法和遗传算法结果对比 如前文分析,优化算法的搜索结果为一组最优 Table 3 Comparison between results of MCMC and Genetic Algorithm 参数,即目标函数达到或接近极小的参数值,而 参数名称MCMC法众数遗传算法优化值 相对误差/% MCMC采样算法的最终结果是参数的后验分布,不 KI2C 0.2000 0.2053 2.6 K20C 0.0518 0.0506 2.5 再是一组参数值.很容易理解,优化算法的最优解应 KIC 2.5500 2.5163 1,3 该位于参数后验分布的高概率密度区域,为此,研究 KIRC 0.1010 0.1006 0.4 NCRB 0.2140 0.2497 14,3 比较了MCMC法不确定分析结果和遗传算法的搜 PCRB 0.0274 0.0246 11.6 索结果24),如前所述,众数代表参数空间的高密度 KDC 0.0370 0.0304 21.6 K2 0.1580 0.1513 4.4 区域的中心,因此表3给出了MCMC法的众数和 K71C 0.0262 0.0304 13,7 优化算法搜索结果的平均值,并计算了它们之间的 K83C 0.0314 0.0298 5.5 相对误差.由表3可知,大多数参数的优化平均值 和参数后验分布的众数之间的差别很小,基本可以 后验分布直方图.从图7(c)可以看出,由于参数相 控制在10%的范围内,个别参数误差较大的原因包 关性的影响,参数NCRB基本呈均匀分布,PCRB同 括:①参数灵敏度较低,如KDC、K71C:②参数相关 样如此,限于篇橱未给出,参数灵敏度的影响在参数 性,如NCRB和PCRB,这2个参数的相关性从参数 后验分布中也可反应出来,如图7(d)中参数KDC 的物理意义便可清楚解释,NCRB为浮游植物的氮 的后验分布,低灵敏度导致参数的不确定性增大.相 碳比,PCRB为浮游植物的磷碳比.参数灵敏度和相 比之下,高灵敏度参数,如K20C和K1C,无论优化 关性的影响从参数后验分布直方图可以更消楚地看 算法,还是MCMC法,均可有效识别,见图7 出,可见当模型存在弱可识别性或不可识别参数时, (a)-(b). 优化算法的搜紫结果可能会失真 可见,MCMC法能有效搜索参数后验分布,适 图7为AM算法全局收敛情况下的部分参数 合于复杂模型的参数识别和不确定性分析, 6 (a) ) Std.Dev"0.60 Mean =2.87 12 N=50000.00 Sid.Dev =0.04 Mean=0.066 N=50000.00 00 0.0130.0440.0750.1060.1370.1680.199 1.A9 1.91 233 2.75 3.173.59 4.01 K20℃ KIC Std.Dev -0.03 (g (④ Mean0 249 N=50000.00 Std.Dev-0.02 Meah=0.042 N=50000.00 0 0.2000.216023302500.2670.2840300 0.0090.0250.0400.0550.0700.0850.101 NCRB KDC 图7参数后验分布直方图 Fig.7 Histogram of parameter posterior distribution 万方数据
l期 环 境 科 学 29 不确定性分析时,采用众数分析相对合理. 如前文分析,优化算法的搜索结果为一组最优 参数,即目标函数达到或接近极小的参数值,而 MCMC采样算法的最终结果是参数的后验分布,不 再是一组参数值.很容易理解,优化算法的最优解应 该位于参数后验分布的高概率密度区域,为此,研究 比较了MCMC法不确定分析结果和遗传算法的搜 索结果_2“,如前所述,众数代表参数空间的高密度 区域的中心,因此表3给出了MCMC法的众数和 优化算法搜索结果的平均值,并计算了它们之间的 相对误差由表3可知,大多数参数的优化平均值 和参数后验分布的众数之间的差别很小,基本可以 控制在10%的范围内,个别参数误差较大的原因包 括:①参数灵敏度较低,如KDC、K71C;②参数相关 性,如NCRB和PCRB,这2个参数的相关性从参数 的物理意义便可清楚解释,NCRB为浮游植物的氮 碳比,PCRB为浮游植物的磷碳比.参数灵敏度和相 关性的影响从参数后验分布直方图可以更清楚地看 出.可见当模型存在弱可识别性或不可识别参数时, 优化算法的搜索结果可能会失真 图7为AM算法全局收敛情况下的部分参数 表3 MCMC法和遗传算法结果对比 Table 3 Comparison betweea results of MCMC and Genetic Algorithm 后验分布直方图.从图7(c)可以看出,由于参数相 关性的影响,参数NCRB基本呈均匀分布,PCRB同 样如此,限于篇幅未给出.参数灵敏度的影响在参数 后验分布中也可反应出来,如图7(d)中参数KDC 的后验分布,低灵敏度导致参数的不确定性增大相 比之下,高灵敏度参数,如K20C和K1C,无论优化 算法,还是MCMC法,均可有效识别,见图7 (a)~(b) 可见,MCMC法能有效搜索参数后验分布,适 合于复杂模型的参数识别和不确定性分析 。狮o 025 0 040 0 055 0 070 0 085 010 XDc 圈7参数后验分布直方图 Fig 7 HⅢ‘gmm of parametcr posterior distfibution 永毫§}g}目 8 6 4 2 0 《目B4F目 崞£分95口上I 万方数据

30 环境 科 学 27卷 1J.Math,5i0sci.,1978,38:247-258 5结论 [9]Hornberger M,Spear P C.Eutrophication in Peel Inlet-I. (I)研究采用自适应Metropolis算法来搜索参 The problem-defining behaviour and mathematical model for the phosphorus scenario[]Wat.Res.,1980.14:29-42. 数后验分布.为考察MCMC法对参数后验分布的搜 [10 Spear RC.Hornberger G M.Eutrophication in Peel Inlet- 索性能和效率,进行了2个案例研究.案例1为一个 Identkion of critical uncertainties vigeneralizedtivity 已知的双峰概率密度函数,案例2为WASP模型在 analysis[J].Wat.Res.,1980.14:43-49 密云水库水质模拟的应用研究,结果表明,MCMC [11】邓义样,王跨,酸斯芸,等.优化、RSA和GLUE方法在非线 性环境模型参数识别中的比较[J].环境科学,2003,24{6): 法能有效搜素参数后验分布,适合于复杂模型的参 915. 数识别和不确定性分析.同时,Gelman收敛判别准 [12]菊诗松,贝叶斯统计IM].北京:中国统计出版社,1999 则计算表明,MCMC采样序列均能稳定收敛到参数 [13]Jorgenscn S E.An improved parameter estimation procedure in 的后验分布上, lake modeling J ]Lake Reservoirs:Rescarch and (2)相比基于随机采样的方法,如RSA法和 manAgement,1998,3:139~142, GLUE法,MCMC法对参数后验分布的搜索,无论 「14]龚光鲁,钱敏平.应用随机过程救程及其在算法与智能计算 中的应用[M].北京:清华大学出板社,2003. 是搜案性能还是瘦索效率,均表现出了独特的优越 [15]Gilks W R,Richardson S,Spiegelhalter D J.Markov chain 性,同时,AM算法可有效处理参数灵敏度和参数相 Monte Carlo in practice[M].London:Chapman Hall,1996. 关性的影响 [16]Smith A F M.Robert G O.Bayesian computation vin the Gibbs 参考文献: sampler and related Markov chain Monte Carlo methods J]. [1】程声通,陈航龄,环境系统分析M.北京:高等教育出版 Journal of Royal Statistical Saciery Series B,1993,55:3-23. 社,1990. [17 Tierney L.Markov-chains for exploring psterior distributions [2 Chen J,Wheater H S.Identification and uncertainty analysis of [J].Annals of Stacistics,1994,22:1701 -1762. soil water retention models using lysimeter data [J].Water [18]Chib S,Greenberg E.Underslanin the Metropolis-Hastings Resources Research.1999.35 (8):2401--2414. algorithm[J].American Statistician.1995.49(4):327335. 【3]刘毅,陈吉宁,杜感飞,环境模型参数识别与不确定性分析 [19]Haario H,Saksman E,Tamminem J.An adaptive Mesropulis 1J」,环境科学,2002,23(6):6~1【. aigorithmfJ).Bernoulli,2001.7(2):223-242. [4 Beck M B.Water Quality Modeling:A Review of the Analysis 20]Roberts G O,Tweedie R L.geometric convergence and central of Unecrtainty[J].Water Resources Research,1987,23 (8): limit theorems for multidimensional Hastings and Metropolis 1393-1442. algorithms[J].Bicmetrika.1996,83:95~110. 5]Omlin M.Reichert P.A comparison of techniques for the [21]Gelman A,Rubin D B.Inference from iterative simulation using extimation of model prediction unceriniaty.Ecological multiple scquences[I'.Statislics Sicience,1992,7 (4):457- Modelling.1999,1l5:45-59. 511, [6 Beven K.Binley A.The future of distributed models:model 22]亚海峰.GS强化下的水库水质模拟及其在密云水库中的应 calibration and uncerteinty prediction ]Hydrological 用研究[D],北京:清华大学,1999。 pr0e.19y2,6:279-298. [23 Ambrose R B,Wool T A,Martin J 1..et al.WASP5.x,A [7]Reichen P.Omlin M.(n the usefulness of overparameterized Hydrudynamic and Water Quality Model Model Theory.User's ecological models[J].Ecological Modelling,1997,95:289~ Manual,and Programmer's Guide[M].Draft:Environmental 299. Research Laboratory,LS Environmental Protection Agency, 8 Tiwari J.Hobbie J.Peterson B.Random differential equations 1993. as modcls of cosystems..Bayesian inference for parameters [24]王建平,程声通,贾海峰.水质模型参数优化的遗传算法实 现及控制参数分析1J.环境科学,2005,26(3):61-65 万方数据
环 境 科 学 27卷 5结论 (1)研究采用自适应Metropolis算法来搜索参 数后验分布为考察MCMC法对参数后验分布的搜 索性能和效率,进行了2个案例研究.案例l为一个 已知的双峰概率密度函数,案例2为WASP模型在 密云水库水质模拟的应用研究结果表明,MCMC 法能有效搜索参数后验分布,适台于复杂模型的参 数识别和不确定性分析同时,Gelman收敛判别准 则计算表明,MCMC采样序列均能稳定收敛到参数 的后验分布上. (2)相比基于随机采样的方法,如RSA法和 GLUE法,MCMC法对参数后验分布的搜索,无论 足搜索性能还是搜索效率,均表现出了独特的优越 性,同时,AM算法可有效处理参数灵敏度和参数相 关性的影响 参考文献: [1]程声通,陈毓龄环境系统分析’M J北京:高等教育出版 社,1990 [2]Chen J,Wheater H S Identification and uncertainty analysis of rail waIer retention models using lysimeter data[J]Water RcsoHrce$R…rcfl,1999,35(8):2401~2414 【3]刘毅.陈吉宁,桂鹏飞环境梗型参数识别与不确定性分析 ¨I环境科学,2002.23(6):6~tI [4] B州k M B Water Quality Modeling:A Review f,r ire Analyais of Uncertainty[J]Wa rer R啪urces Research,1987,23(8): 1393~1442 5 1 Dmlin M,Reiehart P A tuompariMm of techniques for the estimation el model prediction uucerlaiuty i J] Ecdngieal Modelling.1999.115:45~59 [6 Beven K Binley A The future of distributed models:model calibration and uncertainty 0redb:lion『J]tIydmlngieal processes.1992.6:279~298 [7]Reiehar*P,Omlhl M()n tbe usetulness of ovcrparameteriaed ecologicalmodels[J]Ecological Modelling,1997,95:289~ 299 :8]Tiwari J,Hobbie J,Peterson B Random differential equadons as models of e∞systⅢ1s.ⅢBayesian hl{erenoe for par珊eters J:Math Biosei,1978,38:2471 258 Hornberger(j M,SpⅢP C Eutrophication in Peel Inlet—I The problem defining behaviour and mathematical model for Ihe phosphoras scenario[J.Wat Res,1980.14:29~42 Spear R c.Hornberger G M Eutrophication in Peel Inlet-n Idemlf/calkm of critical uncertainties via generalized seetsitivity analysis[J"]War R瞵,1980,14:43—49 邓义祥,王琦,赖斯芸,等优化、RSA和GLUE方法在非线 性环境模型参数识别中的比较[J]环境科学.2003,24(6) 9~15 茆诗拾贝叶斯统计[M]北京:中国统计出版社,1999. Jorgensen S E An iatpmved parameter estimation procedure in lake modeling[J]Lake&Reservoirs:Research and management.1998,3:139~142 龚光鲁,钱敏平应用随机过程教程&其在算法与智能计算 中的应用[M].北京;清华大学出版社,2003 Gilha W R,Richard∞n S,Spie49elha[ter D J Markov chain Monte 1;arlo in practice[M]London:Chapman&Hall,1996 Smith A F M.Robert G O Bayesian computation via the Gibbs sampler and related Marker chain Monte Carlo methodsl Jj Journal ofRoyal Statistical Sc,ciety Series B 1993,55:3~23 Tierney L Matkov—chains for exploring ptnterior distributions [J]Annals of Statistics,1994,22:1701~1762 Chib S,Greenberg E Underslandiitg the Metropolis—Hastings aIgorithm[J]AmerieartStatistician,1995.49(4):327~335 Haafio H,Saksman E,Tamminem J An adaptive Metropolis a[gorithni[J]Bernouiii.200I.,(2)t 223~242 Roberts G O,Tweedie R L}:eomettic convergence and central limit lhe.rems for nmltidimensiotta[Hastings and Metropelis ninerithms[J]Biomet rika,1996,83:95—110 Gc【man A,Ruhin D B Inference from iterative sinmiation using multiple scqoences[J sm出『ics Science,1992,7(4)457— 511 贾海峰GIS强化下的水库水质模拟及其在密百水库L}|的应 用研究[D]北京:清华大学,1999 AmbroseR B,Wool T A,Martin J L.el al WASP5 x,A Hydrvdynamlc and Water Quality Model Model Theory.User’s Manual,and Prog rammer’s Guide[M]Draft:Environmemal Research Laboratory,US Environmental Protection Agency, 1993 王建平,程声通,贾海峰水质模型参数优化的遗传算法实 现厦控制参数分析【J J环境科学。2005 26(3):61~65 o m ¨ 惶¨ H ¨ 坫 " 蜡 伸 孙 “ 控 ∞ H 万方数据

基于MCMC法的水质模型参数不确定性研究 田万方数据 WANFANG DATA 文献链接 作者: 王建平,程声通,贾海峰,WANG Jian-ping, CHENG Sheng-tong, JIA Hai-feng 作者单位: 清华大学环境科学与工程系,北京,100084 刊名: 环境科学STICPK) 英文刊名: ENVIRONMENTAL SCIENCE 年,卷(期): 2006,27(1) 被引用次数: 24次 参考文献(24条) 1.程声通.陈毓龄环境系统分析1990 2.Chen J.Wheater H S Identification and uncertainty analysis of soil water retention models using lysimeter data[外文期刊]1999(08) 3.刘毅.陈吉宁.杜鹏飞环境模型参数识别与不确定性分析[期刊论文]-环境科学2002(06) 4.Beck M B Water Quality Modeling:A Review of the Analysis of Uncertainty[s外文期f刊]I987(O8) 5.0mlin M.Reichert PA comparison of techniques for the estimation of model prediction uncertainty [外文期刊]1999(1) 6.Beven K.Binley A The future of distributed models:model calibration and uncertainty prediction[ 文期刊]1992 7.Reichert P.Omlin M On the usefulness of overparameterized ecological models[]1997(2/3) 8.Tiwari J.Hobbie J.Peterson B Random differential equations as models of ecosystems,Ill Bayesian inference for parameters[外文期f刊]l978 9.Hornberger G M.Spear P C Eutrophication in Peel Inlet-I.The problem-defining behaviour and mathematical model for the phosphorus scenario[外文期刊]l980 10.Spear R C.Hornberger G M Eutrophication in Peel Inlet-II.Identification of critical uncertainties via generalized sensitivity analysis[外文期f刊]l980 1L.邓义祥.王琦.赖斯芸优化、RSA和GLUE方法在非线性环境模型参数识别中的比较[期刊论文]-环境科学 2003(06) 12.茆诗松贝叶斯统计1999 13.Jorgensen S E An improved parameter estimation procedure in lake modeling 1998 14.龚光鲁.钱敏平应用随机过程教程及其在算法与智能计算中的应用2003 15.Gilks W R.Richardson S.Spiegelhalter D J Markov chain Monte Carlo in practice 1996 16.Smith A F M.Robert G O Bayesian computation via the Gibbs sampler and related Markov chain Monte Carlo methods 1993 17.Tierney L Markov-chains for exploring posterior distributions 1994 18.Chib S.Greenberg E Understanding the Metropolis-Hastings algorithm 1995(04) l9.Haario H.Saksman E.Tamminem J An adaptive Metropolis algorithm[外文期刊]200l(02) 20.Roberts G0.Tweedie R L geometric convergence and central limit theorems for multidimensional Hastings and Metropolis algorithms[外文期f刊]1996 2l.Gelman A.Rubin D B Inference from iterative simulation using multiple sequences[外文期f刊] 1992(04)
基于MCMC法的水质模型参数不确定性研究 作者: 王建平, 程声通, 贾海峰, WANG Jian-ping, CHENG Sheng-tong, JIA Hai-feng 作者单位: 清华大学环境科学与工程系,北京,100084 刊名: 环境科学 英文刊名: ENVIRONMENTAL SCIENCE 年,卷(期): 2006,27(1) 被引用次数: 24次 参考文献(24条) 1.程声通.陈毓龄 环境系统分析 1990 2.Chen J.Wheater H S Identification and uncertainty analysis of soil water retention models using lysimeter data[外文期刊] 1999(08) 3.刘毅.陈吉宁.杜鹏飞 环境模型参数识别与不确定性分析[期刊论文]-环境科学 2002(06) 4.Beck M B Water Quality Modeling:A Review of the Analysis of Uncertainty[外文期刊] 1987(08) 5.Omlin M.Reichert P A comparison of techniques for the estimation of model prediction uncertainty [外文期刊] 1999(1) 6.Beven K.Binley A The future of distributed models:model calibration and uncertainty prediction[外 文期刊] 1992 7.Reichert P.Omlin M On the usefulness of overparameterized ecological models[外文期刊] 1997(2/3) 8.Tiwari J.Hobbie J.Peterson B Random differential equations as models of ecosystems,Ⅲ Bayesian inference for parameters[外文期刊] 1978 9.Hornberger G M.Spear P C Eutrophication in Peel Inlet-Ⅰ.The problem-defining behaviour and mathematical model for the phosphorus scenario[外文期刊] 1980 10.Spear R C.Hornberger G M Eutrophication in Peel Inlet-Ⅱ.Identification of critical uncertainties via generalized sensitivity analysis[外文期刊] 1980 11.邓义祥.王琦.赖斯芸 优化、RSA和GLUE方法在非线性环境模型参数识别中的比较[期刊论文]-环境科学 2003(06) 12.茆诗松 贝叶斯统计 1999 13.Jorgensen S E An improved parameter estimation procedure in lake modeling 1998 14.龚光鲁.钱敏平 应用随机过程教程及其在算法与智能计算中的应用 2003 15.Gilks W R.Richardson S.Spiegelhalter D J Markov chain Monte Carlo in practice 1996 16.Smith A F M.Robert G O Bayesian computation via the Gibbs sampler and related Markov chain Monte Carlo methods 1993 17.Tierney L Markov-chains for exploring posterior distributions 1994 18.Chib S.Greenberg E Understanding the Metropolis-Hastings algorithm 1995(04) 19.Haario H.Saksman E.Tamminem J An adaptive Metropolis algorithm[外文期刊] 2001(02) 20.Roberts G O.Tweedie R L geometric convergence and central limit theorems for multidimensional Hastings and Metropolis algorithms[外文期刊] 1996 21.Gelman A.Rubin D B Inference from iterative simulation using multiple sequences[外文期刊] 1992(04)