
第54卷第11期 地球物理学报 Vol.54.No.11 2011年11月 CHINESE JOURNAL OF GEOPHYSICS Nov.,2011 张广智,王丹阳,印兴耀等.基于MCMC的叠前地震反演方法研究.地球物理学报,2011,54(11):2926~2932,DOI:10.3969/j. issn.0001-5733.2011.11.022 Zhang G Z,Wang D Y,Yin X Y,et al.Study on prestack seismic inversion using markov Chain monte carlo.Chinese J. Geophys.(in Chinese),2011,54(11):2926~2932,D0I:10.3969/j.issn.0001-5733.2011.11.022 基于MCMC的叠前地震反演方法研究 张广智,王丹阳,印兴耀,李宁 中国石油大学(华东)地球科学与技术学院,青岛257061 摘要马尔科夫链蒙特卡洛方法(MCMC)是一种启发式的全局寻优算法).它在贝叶斯框架下,利用已有资料 进行约束,既可使最优解满足参数的统计特性,又通过融人的先验信息,提高解的精度:寻优过程可跳出局部最优, 得到全局最优解.利用MCMC方法,可以得到大量来自于后验概率分布的样本,不仅可以得到每个未知参数的估 计值,而且可以得到与之相关的各种不确定性信息.此外,由于算法并不是利用有单一最优解的目标函数,所以结 果对初始值的依赖不强.通过对简单一维层状介质模型的处理,和实际资料的应用,说明利用基于M©tropolis- Hastings算法的MCMC方法进行地震反演,通过对解空间的随机搜索能够得到较好的效果. 关键词非线性反演,MCMC,叠前地震反演,Metropolis-Hastings算法 D0I:10.3969/i.issm.0001-5733.2011.11.022 中图分类号P631 收稿日期2010-04-06,2010-06-28收修定稿 Study on prestack seismic inversion using Markov Chain Monte Carlo ZHANG Guang-Zhi,WANG Dan-Yang,YIN Xing-Yao,LI Ning Shool of Geosciences.China University of Petroleum.Qingdao 257061.China Abstract Markov Chain Monte Carlo method is a heuristic global optimization method.In the Bayesian framework,the optimal solution meets the statistical properties of the parameters with the constraints of data(eg.seismic data,well log);the accuracy of solution is improved with the prior information joined in;optimization process can jump out of local optimum,and ultimately obtain the global optimal solution.Using MCMC methods,we draw a large number of samples from the posterior distribution function.With these samples,we obtain not only the estimates of each unknown variable,but also various types of uncertainty information associated with the estimation.In addition,because of not making use of a objective functions with single optimal solution,the results obtained with MCMC method are independent of the choice of initial values. By testing a 1D layered model and the application of real seismic data in South China,shows the MCMC method based on Metropolis-Hastings algorithm is available and can obtain good results by random searching solution space. Keywords non-linear inversion,Markov Chain Monte Carlo,prestack seismic inversion, Metropolis-Hastings algorithm 基金项目国家油气重大专项(2011ZX05014-001-010HZ)、中国石油科技创新项目(2011D-5006-0301)、中国石油大学(华东)自主创新科研计 划项目(11CX05006A)联合资助. 作者简介: 张广智,男,1971年生,博士,中国石油大学(华东)副教授,主要研究方向为地震储层预测与描述方法研究. 丙高数据ggz@upc.edu.cn
书 第54卷 第11期 2011年11月 地 球 物 理 学 报 CHINESE JOURNAL OF GEOPHYSICS Vol.54,No.11 Nov.,2011 张广智,王丹阳,印兴耀等.基于 MCMC的叠前地震反演方法研究.地球物理学报,2011,54(11):2926~2932,DOI:10.3969/j. issn.00015733.2011.11.022 ZhangGZ,WangD Y,YinX Y,etal.StudyonprestackseismicinversionusingmarkovChainmontecarlo.犆犺犻狀犲狊犲犑. 犌犲狅狆犺狔狊.(inChinese),2011,54(11):2926~2932,DOI:10.3969/j.issn.00015733.2011.11.022 基于 犕犆犕犆的叠前地震反演方法研究 张广智,王丹阳,印兴耀,李 宁 中国石油大学(华东)地球科学与技术学院,青岛 257061 摘 要 马尔科夫链蒙特卡洛方法(MCMC)是一种启发式的全局寻优算法[1] .它在贝叶斯框架下,利用已有资料 进行约束,既可使最优解满足参数的统计特性,又通过融入的先验信息,提高解的精度;寻优过程可跳出局部最优, 得到全局最优解.利用 MCMC方法,可以得到大量来自于后验概率分布的样本,不仅可以得到每个未知参数的估 计值,而且可以得到与之相关的各种不确定性信息.此外,由于算法并不是利用有单一最优解的目标函数,所以结 果对初始值的依赖不强.通过对简单一维层状介质模型的处理,和实际资料的应用,说明 利 用 基 于 Metropolis Hastings算法的 MCMC方法进行地震反演,通过对解空间的随机搜索能够得到较好的效果. 关键词 非线性反演,MCMC,叠前地震反演,MetropolisHastings算法 DOI:10.3969/j.issn.00015733.2011.11.022 中图分类号 P631 收稿日期20100406,20100628收修定稿 基金项目 国家油气重大专项(2011ZX05014001010HZ)、中国石油科技创新项目(2011D50060301)、中国石油大学(华东)自主创新科研计 划项目(11CX05006A)联合资助. 作者简介 张广智,男,1971年生,博士,中国石油大学(华东)副教授,主要研究方向为地震储层预测与描述方法研究. Email:zhanggz@upc.edu.cn 犛狋狌犱狔狅狀狆狉犲狊狋犪犮犽狊犲犻狊犿犻犮犻狀狏犲狉狊犻狅狀狌狊犻狀犵犕犪狉犽狅狏犆犺犪犻狀犕狅狀狋犲犆犪狉犾狅 ZHANGGuangZhi,WANGDanYang,YINXingYao,LINing 犛犺狅狅犾狅犳犌犲狅狊犮犻犲狀犮犲狊,犆犺犻狀犪犝狀犻狏犲狉狊犻狋狔狅犳犘犲狋狉狅犾犲狌犿,犙犻狀犵犱犪狅257061,犆犺犻狀犪 犃犫狊狋狉犪犮狋 MarkovChain MonteCarlomethodisaheuristicglobaloptimizationmethod.Inthe Bayesianframework,theoptimalsolutionmeetsthestatisticalpropertiesoftheparameterswith theconstraintsofdata(eg.seismicdata,welllog);theaccuracyofsolutionisimprovedwiththe priorinformationjoinedin;optimizationprocesscanjumpoutoflocaloptimum,andultimately obtaintheglobaloptimalsolution.Using MCMC methods,wedrawalargenumberofsamples fromtheposteriordistributionfunction.Withthesesamples,weobtainnotonlytheestimatesof eachunknownvariable,butalsovarioustypesofuncertaintyinformationassociated withthe estimation.Inaddition,becauseofnotmakinguseofaobjectivefunctionswithsingleoptimal solution,theresultsobtainedwithMCMCmethodareindependentofthechoiceofinitialvalues. Bytestinga1DlayeredmodelandtheapplicationofrealseismicdatainSouthChina,showsthe MCMCmethodbasedon MetropolisHastingsalgorithmisavailableandcanobtaingoodresults byrandomsearchingsolutionspace. 犓犲狔狑狅狉犱狊 nonlinearinversion, Markov Chain Monte Carlo,prestack seismicinversion, MetropolisHastingsalgorithm 万方数据

11期 张广智等:基于MCMC的登前地震反演方法研究 2927 用π,(t)=P(X,=s,)表示马氏链在t时刻处于 1 引 言 状态s的概率.则对于在时刻1十1马尔科夫链有状态 s的概率π,(t+1)可以由Chapman--Kolomogorov方 叠后地震反演使用全角度多次叠加的地震数 程得到: 据,只能提供种类很少的纵波波阻抗等参数,不能给 π(t+1)=P(X+1=s) 出反映物性、流体特征的参数,在研究储层物性、流 = 体方面受到了限制,因此,常规的叠后反演已经不能 ☒P(X=IX=s)PX=) 满足日益增长的精细储层描述的要求[).与叠后反 =∑P(k→i)e(t)=∑P(k,i)π, (2) 演相比,叠前反演36们具有良好的保真性,可以充分 它可写为更紧凑的矩阵形式:π(t+1)=π(t)P.连 利用叠前地震数据丰富的振幅和旅行时信息,提供 续应用可得到:π(t)=π(O)P,Chapman-Kolomogorov 研究岩性和储层变化规律的更多、更有效的数据体, 方程的这种连续迭代描述了马尔科夫链的发展[2]. 适合进行含油气性反演[-1).笔者根据Fati近似 如果所构造的转移核P(s,s)满足π(s)P(s', 公式,提出一种基于MCMC的叠前反演方法, s)=π(s)P(s,s),那么由其构造的马尔科夫链将 具有唯一的不变分布.这个条件称为细致平衡条件, 1 MCMC方法简介 对于一条存在唯一不变分布的马尔科夫链,当它经 过充分长的迭代后,马尔科夫链将收敛于此,π() MCMC方法属于蒙特卡洛方法.Hammersley and 就可称为平稳分布,对于本文的反演问题,我们希望 Handscomb(1964)将蒙特卡洛方法定义为“有关随 得到所估参数的后验概率分布,所以各个参数的马 机数的实验的实验数学的分支”,其基础是对概率分 尔科夫链应收敛至所估计参数的后验概率分布, 布的直接模拟[1) 1.2 Metropolis-Hastings算法 目前MCMC方法已经广泛应用于理论物理、 常用的构造转移核的方法有Metropolis-Hastings 社会学、生物、医学、人工智能、金融统计、信号通信 算法和Gibbs采样算法.本文选用Metropolis-Hastings 等领域.在过去的十五年间,地球物理学家逐渐开始 算法,其构造马尔科夫链的方法如下[2): 使用MCMC方法进行反演[14~2],直接模拟后验概 若要使π(x)为平稳分布.首先由建议分布 率分布函数(PDF),也就是抽取符合后验PDF的随 q(·|x)产生一个潜在的转移x→x·,然后根据概 机样本,并用这些样本计算解的贝叶斯估计.该方法 率α(x,x·)来决定是否转移,也就是说在潜在转移 也可适用于解决具有复杂的多峰多维PDF的问题. 点x"找到后,以概率a(x,x')接受x'作为链在下 Alberto Malinverno(2o02)利用直流电阻率测 一时刻的状态值.于是,在有了x·后,可从[0,1]的 深数据反演一维地球模型,这是首次将MCMC方 均匀分布上,抽取一个随机数,则 法应用于完全非线性反演问题[2]. X+)= x',w≤a(x,x") 1.1基本原理 x,u>a(x,x') 马尔科夫链蒙特卡洛(MCMC)方法用于对贝 常用的选择是: 叶斯推理中的后验概率分布进行抽样,它通过抽取 收敛于贝叶斯后验分布的随机样本,再对这些样本 a(r.r')=min(1.()q(r'.) 1π(x)q(x,x) 进行统计,来间接得到后验分布的一些性质2]. 易证接受概率的此种形式,可使构造出的转移核满 马尔科夫链是数学中具有马尔科夫性质的离散 足细致平衡条件. 时间过程.若{X,:t≥0}为一随机序列.随机序列所 有可能取到的值组成的集合记为S,称为状态空间.如 2 MCMC叠前反演方法原理 果对于t≥0及任意状态s,s,s。,…,s-1都有 P(X+1=s1X,=s,X-1=s-1,X=,) 在本文提出的方法中,正演部分使用的是 =P(X+1=S|X,=), (1) Zoeppritz方程的Fatti波阻抗近似式[2s.2町. 则称{X:t≥0}为一马尔科夫链2).直观上看,对 R(0)=(1+tan20)rp-872sin2Or; 于马尔科夫过程,要预测将来的唯一有用的信息就 +(472sin20-tan20)ra,(3) 是过程当衙据,而与以前的状态无关. 其中y是横纵波速度的比值的均值,T。、r、ra分别
11期 张广智等:基于 MCMC的叠前地震反演方法研究 1 引 言 叠后地震反演使用全角度多次叠加的地震数 据,只能提供种类很少的纵波波阻抗等参数,不能给 出反映物性、流体特征的参数,在研究储层物性、流 体方面受到了限制,因此,常规的叠后反演已经不能 满足日益增长的精细储层描述的要求[2] .与叠后反 演相比,叠前反演[3~6]具有良好的保真性,可以充分 利用叠前地震数据丰富的振幅和旅行时信息,提供 研究岩性和储层变化规律的更多、更有效的数据体, 适合进行含油气性反演[7~12] .笔者根据 Fatti近似 公式,提出一种基于 MCMC的叠前反演方法. 1 MCMC方法简介 MCMC方法属于蒙特卡洛方法.Hammersleyand Handscomb(1964)将蒙特卡洛方法定义为“有关随 机数的实验的实验数学的分支”,其基础是对概率分 布的直接模拟[13] . 目前 MCMC 方法已经广泛应用于理论物理、 社会学、生物、医学、人工智能、金融统计、信号通信 等领域.在过去的十五年间,地球物理学家逐渐开始 使用 MCMC方法进行反演[14~22],直接模拟后验概 率分布函数(PDF),也就是抽取符合后验 PDF的随 机样本,并用这些样本计算解的贝叶斯估计.该方法 也可适用于解决具有复杂的多峰多维 PDF的问题. AlbertoMalinverno(2002)利用直流电阻率测 深数据反演一维地球模型,这是首次将 MCMC 方 法应用于完全非线性反演问题[23] . 1.1 基本原理 马尔科夫链蒙特卡洛(MCMC)方法用于对贝 叶斯推理中的后验概率分布进行抽样,它通过抽取 收敛于贝叶斯后验分布的随机样本,再对这些样本 进行统计,来间接得到后验分布的一些性质[24] . 马尔科夫链是数学中具有马尔科夫性质的离散 时间过程.若 {犡狋:狋≥0}为一随机序列.随机序列所 有可能取到的值组成的集合记为犛,称为状态空间.如 果对于 狋≥0及任意状态狊犻,狊犼,狊犻0 ,…,狊犻狋-1 都有 犘(犡狋+1 =狊犼狘犡狋 =狊犼,犡狋-1 =狊犻狋-1 ,…,犡0 =狊犻0 ) =犘(犡狋+1 =狊犼狘犡狋 =狊犼), (1) 则称 {犡狋:狋≥0}为一马尔科夫链[25] .直观上看,对 于马尔科夫过程,要预测将来的唯一有用的信息就 是过程当前的状态,而与以前的状态无关. 用π犼(狋)=犘(犡狋 =狊犼)表示马氏链在狋时刻处于 状态狊犼 的概率.则对于在时刻狋+1马尔科夫链有状态 狊犻 的概率π犻(狋+1)可以由 ChapmanKolomogorov方 程得到: π犻(狋+1)=犘(犡狋+1 =狊犻) = ∑犽 犘(犡狋+1 =狊犻狘犡狋 =狊犽)犘(犡狋 =狊犽) = ∑犽 犘(犽→犻)π犽(狋)= ∑犽 犘(犽,犻)π犽, (2) 它可写为更紧凑的矩阵形式:π(狋+1)=π(狋)犘.连 续应用可得到:π(狋)=π(0)犘狋.ChapmanKolomogorov 方程的这种连续迭代描述了马尔科夫链的发展[26] . 如果所构造的转移核 犘(狊,狊′)满足π(狊′)犘(狊′, 狊)=π(狊)犘(狊,狊′),那么由其构造的马尔科夫链将 具有唯一的不变分布.这个条件称为细致平衡条件. 对于一条存在唯一不变分布的马尔科夫链,当它经 过充分长的迭代后,马尔科夫链将收敛于此,π(狊) 就可称为平稳分布.对于本文的反演问题,我们希望 得到所估参数的后验概率分布,所以各个参数的马 尔科夫链应收敛至所估计参数的后验概率分布. 1.2 犕犲狋狉狅狆狅犾犻狊犎犪狊狋犻狀犵狊算法 常用的构造转移核的方法有 MetropolisHastings 算法和 Gibbs采样算法.本文选用 MetropolisHastings 算法,其构造马尔科夫链的方法如下[27]: 若要 使 π(狓)为 平 稳 分 布.首 先 由 建 议 分 布 狇(·狘狓)产生一个潜在的转移狓 →狓 ,然后根据概 率α(狓,狓 )来决定是否转移,也就是说在潜在转移 点狓 找到后,以概率α(狓,狓 )接受狓 作为链在下 一时刻的状态值.于是,在有了狓 后,可从[0,1]的 均匀分布上,抽取一个随机数狌,则 犡(狋+1) = 狓 ,狌≤α(狓,狓 ) 烅狓,狌>α(狓,狓 烄 烆 ) . 常用的选择是: α(狓,狓 )= min 1,π(狓 )狇(狓 ,狓) { π(狓)狇(狓,狓 )}. 易证接受概率的此种形式,可使构造出的转移核满 足细致平衡条件. 2 MCMC叠前反演方法原理 在本 文 提 出 的 方 法 中,正 演 部 分 使 用 的 是 Zoeppritz方程的 Fatti波阻抗近似式[28,29] . 犚(θ珋)= (1+tan2 θ珋)狉p -8γ珔2 sin2 θ珋狉s + (4γ珔2 sin2 θ珋-tan2 θ珋)狉d, (3) 其中γ珔是横纵波速度的比值的均值,狉p、狉s、狉d 分别 2927 万方数据

2928 地球物理学报(Chinese J.Geophys..) 54卷 是纵、横波阻抗反射系数,密度反射系数,并且有 令 -号兴=兴n-,w f)=-∑ -“) Ip=a·p是纵波阻抗,I,=B·p是横波阻抗,是 界面两侧入射角的均值.与其它近似公式相比,该公 -Σa- 式适用于高角度的入射角(小于50°) 则转移概率a(r:,r”)=exp(a'(r,r'),其中 本文中的反问题可以表述如下: a'(r,r')=min{0,f(r")-f(r)}. d=f(rp,r:,ra)+e, (5) 其中d为地震记录,未知参数r。,r,r:的后验概率 3 数值分析 密度为: p(rp,rs,ra I d)=p(rp,rs,ra)p(d I rp,rs,ra), 3.1模型试算 (6) 随机生成51个横波速度3的值,利用经验公式 其中第一项为先验概率密度,假设r。,r,r:相互独 得到纵波速度a和密度p的值3os) 立,且服从高斯分布,其均值分别为少。也,·标 a=1.163+1360m/s, (10) 准差分别为c。,0,则有 p=1.16289a.25tg0.0924 (11) p(rp,rs,ra)=p(r,)·(rs)·p(ra) 入射角为0~30°,间隔为3°,计算得到随角度 1 变化的PP波反射系数R(),与采样间隔为4ms, 50Hz的雷克子波褶积,合成精确的地震记录.加上 -exp 一定量的噪音,得到用于反演的观测地震记录,其信 (2πd) 2 噪比为6.48(SNR-dz代表精确的 地震记录,d出代表用于反演的观测地震记录). (7) 250000次迭代后的估计值,如图1所示,其中3 第二项为似然函数,假设噪音e为均值为0,方 幅图从左至右分别是零偏移距纵波阻抗、横波阻抗 差为σ:的高斯随机噪音,可得到观测地震记录的似 和密度曲线r。,r,r,红色虚线为反演值,黑色实线 然函数为: 线为实际值.从图中可以看出,反演得到的曲线与实 p(d I rp,r.,ra)= 际曲线重合较好,反演效果较好, (2πd) 3.2实际叠前地震资料反演 ×exp(-∑d-f)2) 8) 202 实际资料共有200道,井位于第100道,初始模 为了得到所估参数的后验概率分布p(rpr,ra 型为r。,r,ra的低频趋势,用上述方法进行反演.反 |d),利用Metropolis--Hasting算法来生成马尔科 演测线上的前10个CMP道集如图3所示. 夫链.其建议分布函数取为均匀分布: 在反演过程中,统计井的信息,作为参数的先验 g(ri,r)~U(ri-delta,ri+delta), 信息.图3由左至右分别是由井曲线统计出来的"。, 该建议分布函数满足对称的随机游走,其中”代表 r,r:的直方图.图4是第100道的反演值的直方 Fp,Fs,rd. 图,也就是后验概率分布.图3中拟合出的高斯分布 所以转移概率为: 的标准差分别为0.0162,0.0167,0.0067.图4为 0.0051,0.0064,0.0022.显然后验分布比先验分布 a(ri,r')=min1, π(r)g(r',r:) π(r:)q(r,r') 的范围窄,这是由于似然函数的参与,所以增加了约 束改变了先验分布, (9) 图6(a)是第100道,2190ms处纵波阻抗反射 为了使马尔科夫链最终收敛于未知参数?的后验 系数的马尔科夫链,(b)是2176ms处横波阻抗反射 概率分布,平稳分布应为(rp,r,ra)p(d|rp,rra). 系数的马尔科夫链,(c)是2176ms处密度反射系数 万方数据
地 球 物 理 学 报(ChineseJ.Geophys.) 54卷 是纵、横波阻抗反射系数,密度反射系数,并且有 狉p = 1 2·Δ犐P 犐珔P ,狉s = 1 2·Δ犐s 犐珔s ,狉d = 1 2·Δρ ρ珔 ,(4) 犐P =α·ρ是纵波阻抗,犐s =β·ρ是横波阻抗,θ珋是 界面两侧入射角的均值.与其它近似公式相比,该公 式适用于高角度的入射角(小于50°). 本文中的反问题可以表述如下: 犱=犳(狉p,狉s,狉d)+犲, (5) 其中犱为地震记录.未知参数狉p,狉s,狉d 的后验概率 密度为: 狆(狉p,狉s,狉d狘犱)=狆(狉p,狉s,狉d)狆(犱狘狉p,狉s,狉d), (6) 其中第一项为先验概率密度,假设狉p,狉s,狉d 相互独 立,且服从高斯分布,其均值分别为μ狉p ,μ狉s ,μ狉d ,标 准差分别为σ狉p ,σ狉s ,σ狉d ,则有 狆(狉p,狉s,狉d)=狆(狉p)·狆(狉s)·狆(狉d) = 1 (2πσ 2 狉p ) 狀 2 exp - ∑ (狉p -μ狉p )2 2σ 2 ( 狉p ) × 1 (2πσ 2 狉s ) 狀 2 exp - ∑ (狉s -μ狉s )2 2σ 2 ( 狉s ) × 1 (2πσ 2 狉d ) 狀 2 exp - ∑ (狉d -μ狉d )2 2σ 2 ( 狉d ). (7) 第二项为似然函数,假设噪音犲为均值为0,方 差为σ犲 的高斯随机噪音,可得到观测地震记录的似 然函数为: 狆(犱狘狉p,狉s,狉d)= 1 (2πσ 2 e) 狀 2 ×exp - ∑ (犱-犳(狉p,狉s,狉d))2 2σ ( 犲 2 ). (8) 为了得到所估参数的后验概率分布狆(狉p,狉s,狉d 狘犱),利用 MetropolisHasting算法来生成马尔科 夫链.其建议分布函数取为均匀分布: 狇(狉犻,狉 )~犝(狉犻 -delta,狉犻 +delta), 该建议分布函数满足对称的随机游走,其中狉代表 狉p,狉s,狉d. 所以转移概率为: α(狉犻,狉 )= min 1,π(狉 )狇(狉 ,狉犻) { π(狉犻)狇(狉犻,狉 )} = min 1,π(狉 ) { π(狉犻)}. (9) 为了使马尔科夫链最终收敛于未知参数狉的后验 概率分布,平稳分布应为狆(狉p,狉s,狉d)狆(犱狘狉p,狉s,狉d). 令 犳(狉)= - ∑ (狉p -μ狉p )2 2σ 2 狉p - ∑ (狉s -μ狉s)2 2σ 2 狉s - ∑ (狉d -μ狉d )2 2σ 2 狉d - ∑ (犱-犳(狉p,狉s,狉d))2 2σ 2 犲 . 则 转 移 概 率 α(狉犻,狉 )= exp(α′(狉犻,狉 )),其 中 α′(狉犻,狉 )= min{0,犳(狉 )-犳(狉犻)}. 3 数值分析 3.1 模型试算 随机生成51个横波速度β的值,利用经验公式 得到纵波速度α和密度ρ的值[30,31] . α=1.16β+1360m/s, (10) ρ=1.16289α0.2254 β 0.0924. (11) 入射角为0~30°,间隔为3°,计算得到随角度 变化的 PP波反射系数犚(θ珋),与采样间隔为4ms, 50Hz的雷克子波褶积,合成精确的地震记录.加上 一定量的噪音,得到用于反演的观测地震记录,其信 噪比为6.48(犛犖犚 = σ(犱t- r) σ(犱t- r -犱o- b) ,犱t- r代表精确的 地震记录,犱o- b代表用于反演的观测地震记录). 250000次迭代后的估计值,如图1所示,其中3 幅图从左至右分别是零偏移距纵波阻抗、横波阻抗 和密度曲线狉p,狉s,狉d,红色虚线为反演值,黑色实线 线为实际值.从图中可以看出,反演得到的曲线与实 际曲线重合较好,反演效果较好. 3.2 实际叠前地震资料反演 实际资料共有200道,井位于第100道,初始模 型为狉p,狉s,狉d 的低频趋势,用上述方法进行反演.反 演测线上的前10个 CMP道集如图3所示. 在反演过程中,统计井的信息,作为参数的先验 信息.图3由左至右分别是由井曲线统计出来的狉p, 狉s,狉d 的直方图.图 4 是第 100 道的反演值的直方 图,也就是后验概率分布.图3中拟合出的高斯分布 的标准差分别为 0.0162,0.0167,0.0067.图 4 为 0.0051,0.0064,0.0022.显然后验分布比先验分布 的范围窄,这是由于似然函数的参与,所以增加了约 束改变了先验分布. 图6(a)是第100道,2190ms处纵波阻抗反射 系数的马尔科夫链,(b)是2176ms处横波阻抗反射 系数的马尔科夫链,(c)是2176ms处密度反射系数 2928 万方数据
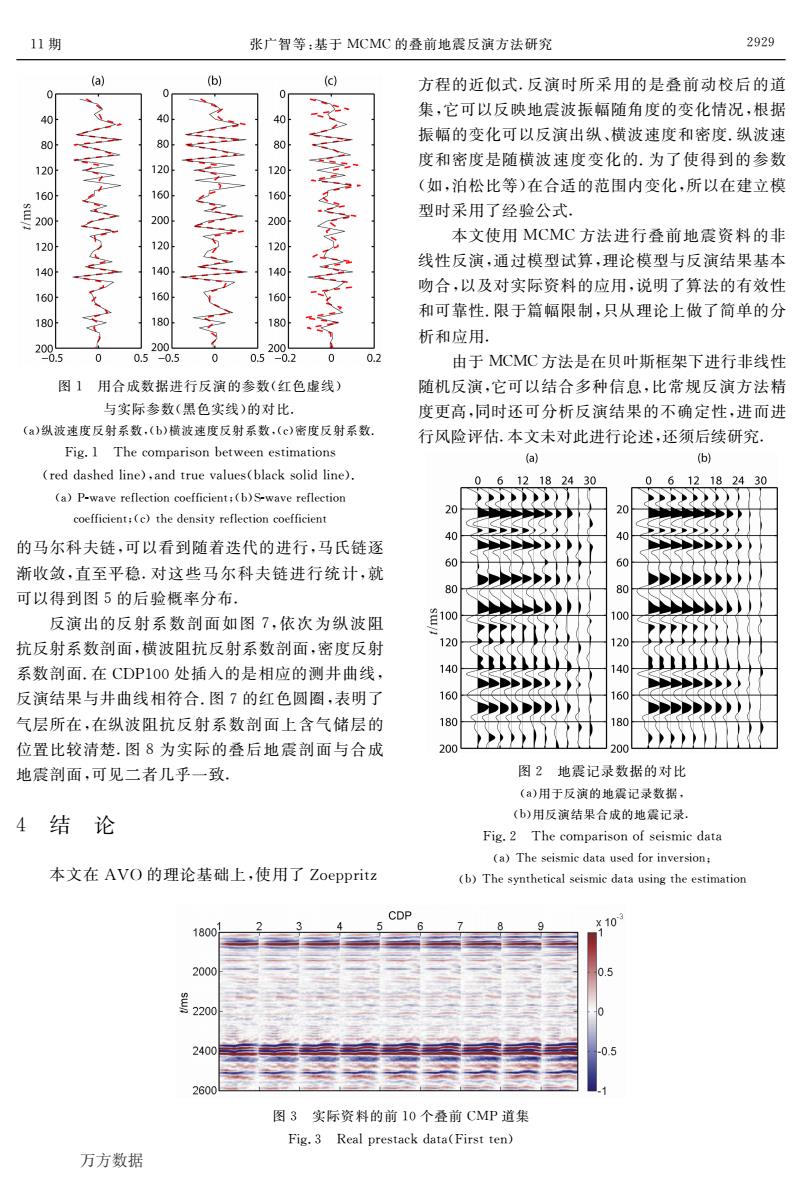
11期 张广智等:基于MCMC的叠前地震反演方法研究 2929 (a) (b) 方程的近似式,反演时所采用的是叠前动校后的道 集,它可以反映地震波振幅随角度的变化情况,根据 振幅的变化可以反演出纵、横波速度和密度.纵波速 80 8 度和密度是随横波速度变化的.为了使得到的参数 120 (如,泊松比等)在合适的范围内变化,所以在建立模 160 160 160 20 型时采用了经验公式, 200 1 本文使用MCMC方法进行叠前地震资料的非 140 0 线性反演,通过模型试算,理论模型与反演结果基本 160 吻合,以及对实际资料的应用,说明了算法的有效性 180 和可靠性.限于篇幅限制,只从理论上做了简单的分 180 200 析和应用. 200 0.5 0.5 -0.5 05-0.2 0.2 由于MCMC方法是在贝叶斯框架下进行非线性 图1用合成数据进行反演的参数(红色虚线) 随机反演,它可以结合多种信息,比常规反演方法精 与实际参数(黑色实线)的对比. 度更高,同时还可分析反演结果的不确定性,进而进 (a)纵波速度反射系数,(b)横波速度反射系数,(c)密度反射系数 行风险评估.本文未对此进行论述,还须后续研究 Fig.1 The comparison between estimations a (b) (red dashed line),and true values(black solid line). 1824 30 1218 24 30 (a)P-wave reflection coefficient:(b)S-wave reflection 20 coefficient:(c)the density reflection coefficient 4 的马尔科夫链,可以看到随着迭代的进行,马氏链逐 60 渐收敛,直至平稳.对这些马尔科夫链进行统计,就 可以得到图5的后验概率分布, 反演出的反射系数剖面如图7,依次为纵波阻 310 抗反射系数剖面,横波阻抗反射系数剖面,密度反射 120 2 系数剖面.在CDP100处插入的是相应的测井曲线, 140 反演结果与井曲线相符合.图7的红色圆圈,表明了 160 60 气层所在,在纵波阻抗反射系数剖面上含气储层的 180 180 位置比较清楚.图8为实际的叠后地震剖面与合成 200 200 地震剖面,可见二者几乎一致. 图2地震记录数据的对比 (a)用于反演的地震记录数据, 4 结 论 (b)用反演结果合成的地震记录. Fig.2 The comparison of seismic data (a)The seismic data used for inversion: 本文在AVO的理论基础上,使用了Zoeppritz (b)The synthetical seismic data using the estimation CDP 1800 2000 2200 2400 2600 图3实际资料的前10个叠前CMP道集 Fig.3 Real prestack data(First ten) 万方数据
11期 张广智等:基于 MCMC的叠前地震反演方法研究 图1 用合成数据进行反演的参数(红色虚线) 与实际参数(黑色实线)的对比. (a)纵波速度反射系数,(b)横波速度反射系数,(c)密度反射系数. Fig.1 Thecomparisonbetweenestimations (reddashedline),andtruevalues(blacksolidline). (a)Pwavereflectioncoefficient;(b)Swavereflection coefficient;(c)thedensityreflectioncoefficient 的马尔科夫链,可以看到随着迭代的进行,马氏链逐 渐收敛,直至平稳.对这些马尔科夫链进行统计,就 可以得到图5的后验概率分布. 反演出的反射系数剖面如图7,依次为纵波阻 抗反射系数剖面,横波阻抗反射系数剖面,密度反射 系数剖面.在 CDP100处插入的是相应的测井曲线, 反演结果与井曲线相符合.图7的红色圆圈,表明了 气层所在,在纵波阻抗反射系数剖面上含气储层的 位置比较清楚.图8为实际的叠后地震剖面与合成 地震剖面,可见二者几乎一致. 4 结 论 本文在 AVO 的理论基础上,使用了Zoeppritz 方程的近似式.反演时所采用的是叠前动校后的道 集,它可以反映地震波振幅随角度的变化情况,根据 振幅的变化可以反演出纵、横波速度和密度.纵波速 度和密度是随横波速度变化的.为了使得到的参数 (如,泊松比等)在合适的范围内变化,所以在建立模 型时采用了经验公式. 本文使用 MCMC方法进行叠前地震资料的非 线性反演,通过模型试算,理论模型与反演结果基本 吻合,以及对实际资料的应用,说明了算法的有效性 和可靠性.限于篇幅限制,只从理论上做了简单的分 析和应用. 由于 MCMC方法是在贝叶斯框架下进行非线性 随机反演,它可以结合多种信息,比常规反演方法精 度更高,同时还可分析反演结果的不确定性,进而进 行风险评估.本文未对此进行论述,还须后续研究. 图2 地震记录数据的对比 (a)用于反演的地震记录数据, (b)用反演结果合成的地震记录. Fig.2 Thecomparisonofseismicdata (a)Theseismicdatausedforinversion; (b)Thesyntheticalseismicdatausingtheestimation 图3 实际资料的前10个叠前 CMP道集 Fig.3 Realprestackdata(Firstten) 2929 万方数据
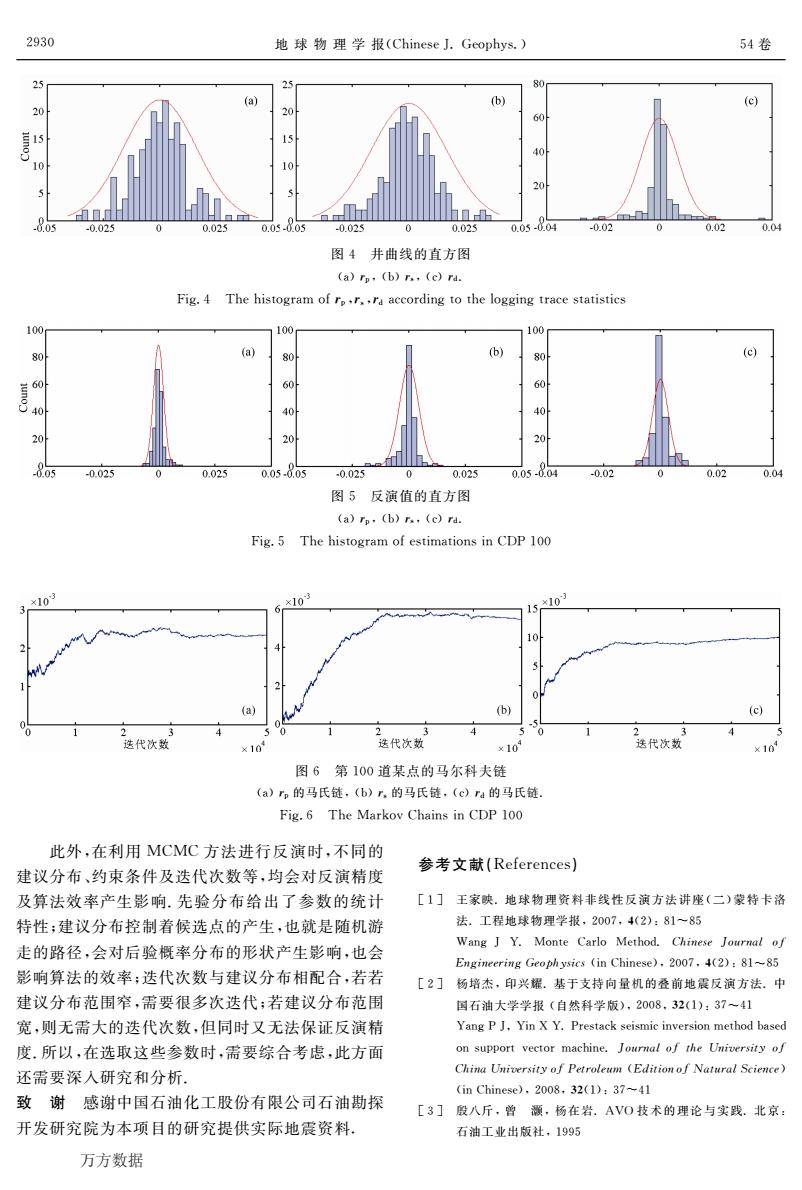
2930 地球物理学报(Chinese J.Geophys..) 54卷 25 80 (a) (b) 20 20 (e) 60 15 15 40 10 10 20 a几 -0.05 -0.025 0.025 0.05-005 -0.025 0.025 005.804 -0.02 0.02 0.04 图4井曲线的直方图 (a)rp,(b)r..(c)ra. Fig.4 The histogram of rp.r..ra according to the logging trace statistics 100 100 100 80 (a) 80H (b) g (c) 60 40 40h 40 20 20 8.05 -0.025 0 0.025 0.05-0.05 0,025 0.025 0.05-004 -0.02 0.02 0.04 图5反演值的直方图 (a)rp.(b)r..(c)ra. Fig.5 The histogram of estimations in CDP 100 103 *103 103 6 10 (a) (b) (c) 2 4 5 4 2 迭代次致 ×10 迭代次数 ×10 迭代次数 ×10 图6第100道某点的马尔科夫链 (a)rp的马氏链,(b)r的马氏链,(c)ra的马氏链. Fig.6 The Markov Chains in CDP 100 此外,在利用MCMC方法进行反演时,不同的 参考文献(References) 建议分布、约束条件及迭代次数等,均会对反演精度 及算法效率产生影响.先验分布给出了参数的统计 [1]王家映.地球物理资料非线性反演方法讲座(二)蒙特卡洛 特性;建议分布控制着候选点的产生,也就是随机游 法.工程地球物理学报,2007,4(2):81一85 走的路径,会对后验概率分布的形状产生影响,也会 Wang J Y.Monte Carlo Method.Chinese Journal of Engineering Geophysics (in Chinese),2007,4(2):81~85 影响算法的效率;迭代次数与建议分布相配合,若若 [2]杨培杰,印兴耀.基于支持向量机的叠前地震反演方法.中 建议分布范围窄,需要很多次迭代;若建议分布范围 国石油大学学报(自然科学版),2008,32(1):37~41 宽,则无需大的迭代次数,但同时又无法保证反演精 Yang P J.Yin X Y.Prestack seismic inversion method based 度.所以,在选取这些参数时,需要综合考虑,此方面 on support vector machine.Journal of the University of 还需要深入研究和分析. China University of Petroleum (Edition of Natural Science) (in Chinese),2008,32(1):37-41 致谢感谢中国石油化工股份有限公司石油勘探 [3]殷八斤,曾灏,杨在岩.AVO技术的理论与实践.北京: 开发研究院为本项目的研究提供实际地震资料, 石油工业出版社,1995 万方数据
地 球 物 理 学 报(ChineseJ.Geophys.) 54卷 图4 井曲线的直方图 (a)狉p,(b)狉s,(c)狉d. Fig.4 Thehistogramof狉p,狉s,狉daccordingtotheloggingtracestatistics 图5 反演值的直方图 (a)狉p,(b)狉s,(c)狉d. Fig.5 ThehistogramofestimationsinCDP100 图6 第100道某点的马尔科夫链 (a)狉p 的马氏链,(b)狉s 的马氏链,(c)狉d 的马氏链. Fig.6 TheMarkovChainsinCDP100 此外,在利用 MCMC方法进行反演时,不同的 建议分布、约束条件及迭代次数等,均会对反演精度 及算法效率产生影响.先验分布给出了参数的统计 特性;建议分布控制着候选点的产生,也就是随机游 走的路径,会对后验概率分布的形状产生影响,也会 影响算法的效率;迭代次数与建议分布相配合,若若 建议分布范围窄,需要很多次迭代;若建议分布范围 宽,则无需大的迭代次数,但同时又无法保证反演精 度.所以,在选取这些参数时,需要综合考虑,此方面 还需要深入研究和分析. 致 谢 感谢中国石油化工股份有限公司石油勘探 开发研究院为本项目的研究提供实际地震资料. 参考文献(References) [1] 王家映.地球物理资料非线性反演方法讲座(二)蒙特卡洛 法.工程地球物理学报,2007,4(2):81~85 Wang J Y. Monte Carlo Method.犆犺犻狀犲狊犲 犑狅狌狉狀犪犾 狅犳 犈狀犵犻狀犲犲狉犻狀犵犌犲狅狆犺狔狊犻犮狊 (inChinese),2007,4(2):81~85 [2] 杨培杰,印兴耀.基于支持向量机的叠前地震反演方法.中 国石油大学学报 (自然科学版),2008,32(1):37~41 YangPJ,YinXY.Prestackseismicinversionmethodbased onsupportvector machine.犑狅狌狉狀犪犾狅犳狋犺犲 犝狀犻狏犲狉狊犻狋狔狅犳 犆犺犻狀犪犝狀犻狏犲狉狊犻狋狔狅犳犘犲狋狉狅犾犲狌犿 (犈犱犻狋犻狅狀狅犳犖犪狋狌狉犪犾犛犮犻犲狀犮犲) (inChinese),2008,32(1):37~41 [3] 殷八斤,曾 灏,杨在岩.AVO 技术的理论与实践.北京: 石油工业出版社,1995 2930 万方数据
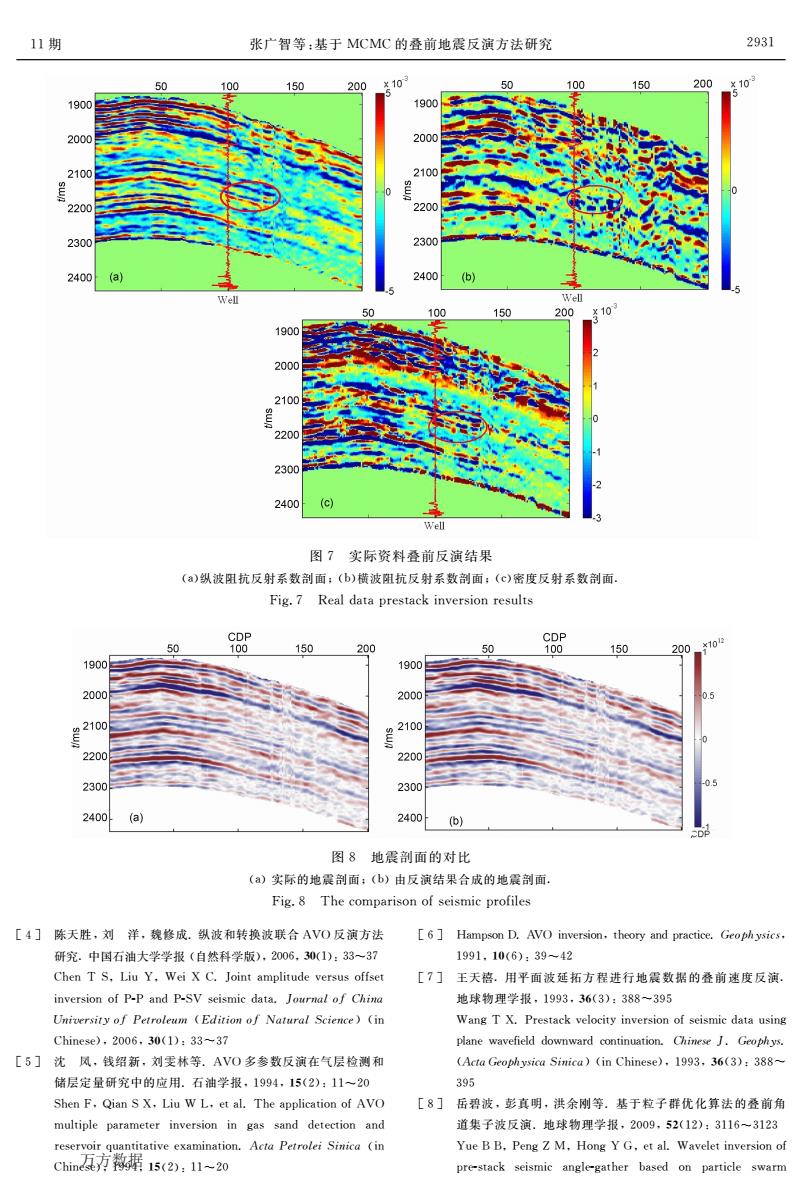
11期 张广智等:基于MCMC的叠前地震反演方法研究 2931 50 100 150 200 10 50 150 200 10 1900 1900 2000 200 2100 2100 2200 2200 2300 2300 2400 (a) 2400 (b) Well Well 100 150 200 10 1900 2000 2100 2200 2300 2400 (c) Well 图7实际资料叠前反演结果 (a)纵波阻抗反射系数剖面,(b)横波阻抗反射系数剖面,(c)密度反射系数剖面 Fig.7 Real data prestack inversion results CDE CDP 50 100 150 200 50 100 150 200 *102 1900 1900 2000 2000 05 2100 2200 2200 2300 2300 2400 (a) 2400 (b) 图8地震剖面的对比 ()实际的地震剖面:(b)由反演结果合成的地震剖面. Fig.8 The comparison of seismic profiles [4]陈天胜,刘洋,魏修成.纵波和转换波联合AVO反演方法 [6]Hampson D.AVO inversion.theory and practice.Geophysics. 研究.中国石油大学学报(自然科学版),2006,30(1):33-37 1991.10(6):39-42 Chen T S,Liu Y,Wei X C.Joint amplitude versus offset [7]王天禧.用平面波延拓方程进行地震数据的叠前速度反演. inversion of P-P and P-SV seismic data.Journal of China 地球物理学报,1993,36(3):388-395 University of Petroleum (Edition of Natural Science)(in Wang T X.Prestack velocity inversion of seismic data using Chinese),2006,30(1):33-37 plane wavefield downward continuation.Chinese J.Geophys. [5]沈风,钱绍新,刘雯林等.AVO多参数反演在气层检测和 (Acta Geophysica Sinica)(in Chinese),1993.36(3):388- 储层定量研究中的应用.石油学报,1994,15(2):11~20 395 Shen F.Qian S X.Liu W L.et al.The application of AVO [8]岳碧波,彭真明,洪余刚等.基于粒子群优化算法的叠前角 multiple parameter inversion in gas sand detection and 道集子波反演.地球物理学报,2009,52(12):3116-3123 reservoir quantitative examination.Acta Petrolei Sinica (in Yue BB.Peng Z M,Hong Y G.et al.Wavelet inversion of chin互方据15(2):11~20 pre-stack seismic angle-gather based on particle swarm
11期 张广智等:基于 MCMC的叠前地震反演方法研究 图7 实际资料叠前反演结果 (a)纵波阻抗反射系数剖面;(b)横波阻抗反射系数剖面;(c)密度反射系数剖面. Fig.7 Realdataprestackinversionresults 图8 地震剖面的对比 (a)实际的地震剖面;(b)由反演结果合成的地震剖面. Fig.8 Thecomparisonofseismicprofiles [4] 陈天胜,刘 洋,魏修成.纵波和转换波联合 AVO 反演方法 研究.中国石油大学学报 (自然科学版),2006,30(1):33~37 ChenTS,Liu Y,WeiX C.Jointamplitudeversusoffset inversionofPPandPSVseismicdata.犑狅狌狉狀犪犾狅犳犆犺犻狀犪 犝狀犻狏犲狉狊犻狋狔狅犳犘犲狋狉狅犾犲狌犿 (犈犱犻狋犻狅狀狅犳 犖犪狋狌狉犪犾犛犮犻犲狀犮犲)(in Chinese),2006,30(1):33~37 [5] 沈 凤,钱绍新,刘雯林等.AVO 多参数反演在气层检测和 储层定量研究中的应用.石油学报,1994,15(2):11~20 ShenF,QianSX,LiuW L,etal.TheapplicationofAVO multiple parameter inversion in gas sand detection and reservoirquantitativeexamination.犃犮狋犪犘犲狋狉狅犾犲犻犛犻狀犻犮犪 (in Chinese),1994,15(2):11~20 [6] HampsonD.AVOinversion,theoryandpractice.犌犲狅狆犺狔狊犻犮狊, 1991,10(6):39~42 [7] 王天禧.用平面波延拓方程进行地震数据的叠前速度反演. 地球物理学报,1993,36(3):388~395 WangTX.Prestackvelocityinversionofseismicdatausing planewavefielddownwardcontinuation.犆犺犻狀犲狊犲犑.犌犲狅狆犺狔狊. (犃犮狋犪犌犲狅狆犺狔狊犻犮犪犛犻狀犻犮犪)(inChinese),1993,36(3):388~ 395 [8] 岳碧波,彭真明,洪余刚等.基于粒子群优化算法的叠前角 道集子波反演.地球物理学报,2009,52(12):3116~3123 YueBB,PengZ M,HongYG,etal.Waveletinversionof prestack seismic anglegather based on particle swarm 2931 万方数据

2932 地球物理学报(Chinese J.Geophys..) 54卷 optimization algorithm.Chinese J.Geophys.(in Chinese). waveform inversion and corresponding uncertainty analysis. 2009,52(12):3116-3123 Ge0hys.J.Imt.,2009,177(1):14~32 [9]杨培杰,印兴耀.非线性二次规划贝叶斯叠前反演.地球物 [19]Wang D Y.Zhang G Z.AVO simultaneous inversion using 理学报,2008,51(6):1876~1882 Markov Chain Monte Carlo.In:SEG 80th Annual Meeting. Yang P J.Yin X Y.Non-linear quadratic programming Denver.Colorado.2010 Bayesian prestack inversion.Chinese J.Geophys.(in Chinese), [20]Keilis-Borok V I.Yanovskaya T B.Inverse problems of 2008,51(6):1876-1882 seismology.Geophys.J.,1967,13(1/3):223-234 [10]路鹏飞,杨长春,郭爱华等.改进的模拟退火算法及其在叠 [21]Press F.Earth models obtained by Monte Carlo inversion.J. 前储层参数反演中的应用.地球物理学进展,2008,23(1): Geophy%.Res.,1968,73(16):5223-5234 104-109 [22]王辉,张玉芬.基于模型的叠前数据多参数非线性反演, Lu P F,Yang CC.Guo A H.et al.Modified simulated 岩性油气藏,2008,20(2):108-113 annealing algorithm and its application in pre-stack inversion Wang H.Zhang Y F.Model-based multi-parameters non- of reservoir parameters.Progress in Geophysics.2008.23 linear inversion method in prestack domain.Lithologic (1):104-109 Reservoirs (in Chinese).2008,20(2):108~113 [11]黄伟传,杨长春,王度飞.利用叠前地震数据预测裂缝储层 [23]Malinverno A.Parsimonious Bayesian Markov chain Monte 的应用研究.地球物理学进展,2007,22(5):1602~1606 Carlo inversion in a nonlinear geophysical problem.Geophys. Huang WC.Yang C C.The application of pre-stack seismic J.Imt.,2002,151(3):675-688 data in predicting the fractured reservoir.Progress in Geophysics. [24]Tarantola A.Inverse Problem Theory.New York:Elsevier 2007,22(5):1602-1606 Sci,1987 [12]尚水生,杨长春,王真理等.塔里木盆地卡4区块AV0研 [25]赵琪.MCMC方法研究.山东:山东大学[博士论文, 究.地球物理学进展,2007,22(5):1408~1415 2007.11-18 Shang Y S.Yang CC.Wang Z L.et aL.AVO research in [26]Ro3sSM.统计模拟.王兆军等译.第四版.北京:人民邮电 Ka-4 region of Tarim basin.Progress in Geophysics (in 出版社,2007.203-206 Chinese),2007,22(5):1408-1415 [27]朱嵩.基于贝叶斯推理的环境水力学反问题研究.浙江: [13]Hammersley J M.Handscomb D C.Monte Carlo Methods. 浙江大学[博士论文],2008.63~90 New York:Chapman and Hall,1964. [28]Fatti J L.Smith G C.Vail P J,et al.Detection of gas in [14]Grandis H.Menvielle M,Roussignol M.Bayesian inversion sandstone reservoirs using AVO analysis:A 3-D seismic case with Markov chains-I The magnetotelluric one-dimensional history using the Geostack technique.Geophysics.1994.59 case.Geophys.J.It.,1999,138(3),757~768 (9):1362~1376. [15]Malinverno A.Leaney S.A Monte Carlo method to quantify [29]郑晓东.Zoeppritz方程的近似及其应用.石油地球物理物 uncertainty in the inversion of zero-offset VSP data.In:SEG 探,1991,26(2):129~144 70th Annual Meeting.Calgary.Alberta.2000 [30]Castagna J P.Batzle M L.Eastwood R L.Relationships [16]Chen J S.Joint inversion of seismic AVO and EM data for between compressional-wave and shear-wave velocities in gas saturation estimation using a sampling-based stochastic clastic silicate rocks.Geophysics,1985.50(4):571~581 model.In:SEG 74th Annual Meeting.Denver,Colorado. [31]马中高,解吉高.岩石的纵、横波速度与密度的规律研究.地 2004 球物理学进展,2005,20(4),905-910 [17]Chen J S.Hoversten G M.Vasco D.et al.A Bayesian model Ma Z G.Xie J G.Relationship among compressional wave, for gas saturation estimation using marine seismic AVA and shear wave velocities and density of rocks.Progress in CSEM data.Geophysics.2007,72(2):85~95 Geophysics,2005,20(4),905~910 [18]Hong T C.Sen M K.A new MCMC algorithm for seismic (本文编辑刘少华) 万方数据
地 球 物 理 学 报(ChineseJ.Geophys.) 54卷 optimizationalgorithm.犆犺犻狀犲狊犲犑.犌犲狅狆犺狔狊.(inChinese), 2009,52(12):3116~3123 [9] 杨培杰,印兴耀.非线性二次规划贝叶斯叠前反演.地球物 理学报,2008,51(6):1876~1882 Yang P J,Yin X Y.Nonlinearquadratic programming Bayesianprestackinversion.犆犺犻狀犲狊犲犑.犌犲狅狆犺狔狊.(inChinese), 2008,51(6):1876~1882 [10] 路鹏飞,杨长春,郭爱华等.改进的模拟退火算法及其在叠 前储层参数反演中的应用.地球物理学进展,2008,23(1): 104~109 LuP F,YangC C,Guo A H,etal.Modifiedsimulated annealingalgorithmanditsapplicationinprestackinversion ofreservoirparameters.犘狉狅犵狉犲狊狊犻狀犌犲狅狆犺狔狊犻犮狊,2008,23 (1):104~109 [11] 黄伟传,杨长春,王彦飞.利用叠前地震数据预测裂缝储层 的应用研究.地球物理学进展,2007,22(5):1602~1606 HuangW C,YangCC.Theapplicationofprestackseismic datainpredictingthefracturedreservoir.犘狉狅犵狉犲狊狊犻狀犌犲狅狆犺狔狊犻犮狊, 2007,22(5):1602~1606 [12] 尚永生,杨长春,王真理等.塔里木盆地卡4区块 AVO 研 究.地球物理学进展,2007,22(5):1408~1415 ShangYS,YangCC,WangZL,etal.AVOresearchin Ka4region of Tarim basin.犘狉狅犵狉犲狊狊犻狀 犌犲狅狆犺狔狊犻犮狊 (in Chinese),2007,22(5):1408~1415 [13] HammersleyJM,HandscombDC.MonteCarlo Methods. NewYork:ChapmanandHall,1964. [14] GrandisH,MenvielleM,RoussignolM.Bayesianinversion with MarkovchainsI The magnetotelluriconedimensional case.犌犲狅狆犺狔狊.犑.犐狀狋.,1999,138(3),757~768 [15] MalinvernoA,LeaneyS.A MonteCarlomethodtoquantify uncertaintyintheinversionofzerooffsetVSPdata.In:SEG 70thAnnualMeeting,Calgary,Alberta,2000 [16] ChenJS.JointinversionofseismicAVOandEM datafor gassaturationestimationusingasamplingbasedstochastic model.In:SEG74th AnnualMeeting,Denver,Colorado, 2004 [17] ChenJS,HoverstenG M,VascoD,etal.ABayesianmodel forgassaturationestimationusingmarineseismicAVAand CSEMdata.犌犲狅狆犺狔狊犻犮狊,2007,72(2):85~95 [18] HongTC,Sen M K.Anew MCMCalgorithmforseismic waveforminversionandcorrespondinguncertaintyanalysis. 犌犲狅狆犺狔狊.犑.犐狀狋.,2009,177(1):14~32 [19] WangD Y,ZhangGZ.AVOsimultaneousinversionusing MarkovChainMonteCarlo.In:SEG80thAnnualMeeting, Denver,Colorado,2010 [20] KeilisBorok V I,Yanovskaya T B.Inverseproblemsof seismology.犌犲狅狆犺狔狊.犑.,1967,13(1/3):223~234 [21] PressF.EarthmodelsobtainedbyMonteCarloinversion.犑. 犌犲狅狆犺狔狊.犚犲狊.,1968,73(16):5223~5234 [22] 王 辉,张玉芬.基于模型的叠前数据多参数非线性反演, 岩性油气藏,2008,20(2):108~113 Wang H,Zhang Y F.Modelbased multiparametersnon linearinversion method in prestack domain.犔犻狋犺狅犾狅犵犻犮 犚犲狊犲狉狏狅犻狉狊 (inChinese),2008,20(2):108~113 [23] MalinvernoA.ParsimoniousBayesian Markovchain Monte Carloinversioninanonlineargeophysicalproblem.犌犲狅狆犺狔狊. 犑.犐狀狋.,2002,151(3):675~688 [24] TarantolaA.InverseProblem Theory.New York:Elsevier Sci,1987 [25] 赵 琪.MCMC 方 法 研 究.山 东:山 东 大 学 [博 士 论 文〗, 2007.11~18 [26] RossSM.统计模拟.王兆军等译.第四版.北京:人民邮电 出版社,2007.203~206 [27] 朱 嵩.基于贝叶斯推理的环境水力学反问题研究.浙江: 浙江大学 [博士论文〗,2008.63~90 [28] FattiJL,SmithG C,VailPJ,etal.Detectionofgasin sandstonereservoirsusingAVOanalysis:A3Dseismiccase historyusingtheGeostacktechnique.犌犲狅狆犺狔狊犻犮狊,1994,59 (9):1362~1376. [29] 郑晓东.Zoeppritz方程的近似及其应用.石油地球物理勘 探,1991,26(2):129~144 [30] CastagnaJP,Batzle M L,Eastwood R L.Relationships between compressionalwave and shearwave velocitiesin clasticsilicaterocks.犌犲狅狆犺狔狊犻犮狊,1985,50(4):571~581 [31] 马中高,解吉高.岩石的纵、横波速度与密度的规律研究.地 球物理学进展,2005,20(4),905~910 MaZG,XieJG.Relationshipamongcompressionalwave, shear wave velocities and density ofrocks.犘狉狅犵狉犲狊狊犻狀 犌犲狅狆犺狔狊犻犮狊,2005,20(4),905~910 (本文编辑 刘少华) 2932 万方数据