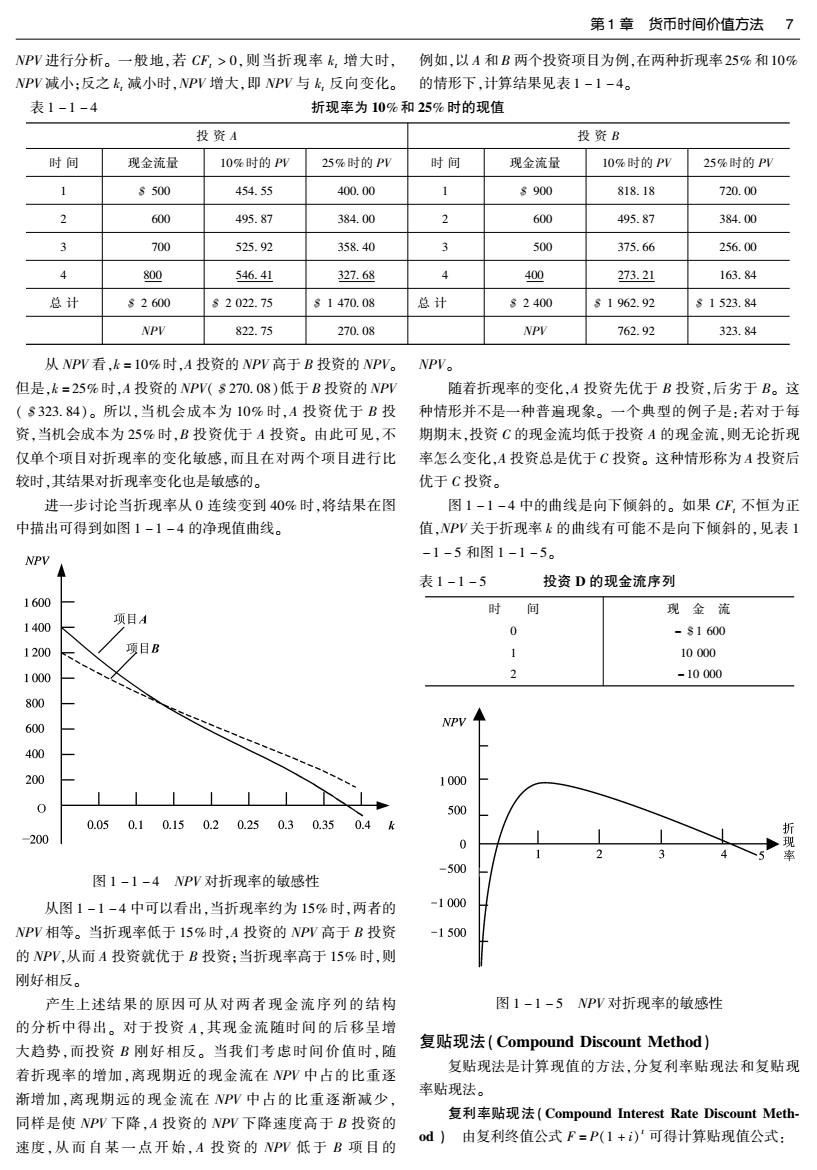
第1章货币时间价值方法7 NPV进行分析。一般地，若CF,>0,则当折现率k,增大时， 例如，以A和B两个投资项目为例，在两种折现率25%和10% NPV减小：反之k,减小时，NPV增大，即NPV与k,反向变化。 的情形下，计算结果见表1-1-4。 表1-1-4 折现率为10%和25%时的现值 投资A 投资B 时间 现金流量 10%时的PV 25%时的PV 时间 现金流量 10%时的PV 25%时的PV s500 454.55 400.00 1 8900 818.18 720.00 2 600 495.87 384.00 2 600 495.87 384.00 3 700 525.92 358.40 3 500 375.66 256.00 4 800 546.41 327.68 4 400 273.21 163.84 总计 82600 S2022.75 s1470.08 总计 82400 s1962.92 81523.84 NPV 822.75 270.08 NPV 762.92 323.84 从NPV看，k=10%时，A投资的NPV高于B投资的NPV。 NP。 但是，k=25%时，A投资的NPV(s270.08)低于B投资的NPV 随着折现率的变化，A投资先优于B投资，后劣于B。这 (S323.84)。所以，当机会成本为10%时，A投资优于B投 种情形并不是一种普遍现象。一个典型的例子是：若对于每 资，当机会成本为25%时，B投资优于A投资。由此可见，不 期期末，投资C的现金流均低于投资A的现金流，则无论折现 仅单个项目对折现率的变化敏感，而且在对两个项目进行比 率怎么变化，A投资总是优于C投资。这种情形称为A投资后 较时，其结果对折现率变化也是敏感的。 优于C投资。 进一步讨论当折现率从0连续变到40%时，将结果在图 图1-1-4中的曲线是向下倾斜的。如果CF,不恒为正 中描出可得到如图1-1-4的净现值曲线。 值，NPV关于折现率k的曲线有可能不是向下倾斜的，见表1 -1-5和图1-1-5。 NPV 表1-1-5 投资D的现金流序列 1600 时 间 现金流 项目A 1400 0 -s1600 1200 项目B 1 10000 1000 2 -10000 800 600 NPV 400 200 1000 0 500 0.050.10.150.20.250.30.35 0.4k 折 200 0 -500 图1-1-4NPV对折现率的敏感性 从图1-1-4中可以看出，当折现率约为15%时，两者的 -1000 NPV相等。当折现率低于15%时，A投资的NPV高于B投资 -1500 的NPV,从而A投资就优于B投资：当折现率高于15%时，则 刚好相反。 产生上述结果的原因可从对两者现金流序列的结构 图1-1-5NPV对折现率的敏感性 的分析中得出。对于投资A,其现金流随时间的后移呈增 大趋势，而投资B刚好相反。当我们考虑时间价值时，随 复贴现法(Compound Discount Method)】 着折现率的增加，离现期近的现金流在NPV中占的比重逐 复贴现法是计算现值的方法，分复利率贴现法和复贴现 渐增加，离现期远的现金流在NPV中占的比重逐渐减少， 率贴现法。 同样是使NPV下降，A投资的NPV下降速度高于B投资的 复利率贴现法(Compound Interest Rate Discount Meth- od)由复利终值公式F=P(1+)'可得计算贴现值公式： 速度，从而自某一点开始，A投资的NPV低于B项目的