
第一篇 金融定量分析方法 分析金融学发端于20世纪50年代初,其标志是马柯维茨(H Markowitz)投资组合理论的发表。在此之前,金融学的研究基本是描述性 的,较少使用数量分析。其后,莫迪利亚尼(F.Modigliani)和米勒(M. Miller)于1958年在研究企业资本结构与企业价值关系(即著名的MM理 论)时,提出了“无套利均衡分析(No-Arbitiage)”方法,则被称为现代金融 学真正的方法论革命,从而也成为金融工程面向产品设计、研发与操作的 基本分析技术,构成了现代金融理论的基石。1973年布莱克(F.Black)和 斯科尔斯(M.Scholes)推导出期权定价模型,与马柯维茨的工作一起被称 为“华尔街的两次数学革命”。随着计算机软件的发展,辅之以信息技术, 分析金融学得到了长足发展。 金融定量分析属于分析金融学,是分析金融学的重要研究方法和分析 工具。它是以统计为基础,数学方法为手段,金融理论为指导,考察金融行 为中的各种数量关系,预测金融发展趋势,检验金融决策效果的工具。它 既运用分析金融学的理论模型,又像金融工程学那样大量采用图解、数值 计算和仿真技术等工程手段来研究问题。大体包括四个基本步骤,即建立 模型、估计参数、验证理论和运用模型。(1)建立模型,是根据金融理论所 考察的现象,找出金融变量间的因果关系及相互联系。把问题作为因变 量,主要相关因素作为自变量,非主要因素归入随机项,按照它们的结构关 系,采用一组或多组方程或不等式表示:(2)估计参数,是根据需要估计出 模型的参数,采用相应的计量方法;(3)验证理论,是运用数理统计中关于 假设验证的原理,验证估计出来的参数与理论预期结果是否一致,所建立 的模型是否符合实际:(4)运用模型分析金融行为和预测未来。模型既可 运用于微观金融分析、中观金融分析,也可运用于宏观金融分析。 金融定量分析方法,作为开篇,为全书提供了方法论基础。本篇收录 可量化的词条309个,按货币时间价值方法、金融预测分析方法、金融决策 分析方法、金融财会分析方法、金融统计分析方法和金融信息分析方法的 顺序,依次进行分析讨论。 需要说明的是,本书在运用数学语言表述问题的同时,也适当地辅以 文字形式的描述与证明,以便适应金融界更多读者的需要

第1章货币时间价值方法3 第1章 货币时间价值方法 货币时间价值(Time Value of Money)是指货币价值对时间的函数关系。在金融定量分析中,货币时间价 值方法是一个非常重要的工具。金融市场上存在着大量的、各种各样的金融资产,每种金融资产都有其特定 的收益形式。如存款的利息、债券的利息、大颜定期存单的利息以及股票的股息等等。通常我们把这些资产 的收益统称为利息,把它们和各自本金之间的比率关系称为利率。在经济学中把利率称为“货币的价格”。正 是由于利息和利率的产生,使今天的货币和昨天等颜的货币的价值不再相等,因为货币存在银行里或贷给别 人,会产生利息。利息随时间推移而不断增加,附在本金上便使今天的货币颜随着时间的推移而不断增加。 货币的时间价值以复利表示,即P。=P(1+)”。式中P。为货币将来值,P。为初始值,i为年利率,n为年份 数。可见,如果利率一定,货币的价值的大小就取决于时间。这里的分析是抽象的。实质上,货币本身并不会 自动增加价值,货币的时间价值反映的是人们对货币资金的利用效果。本章先从利率公式计算入手,而后分 析单利、复利,再分析年金一更为复杂的货币时间价值模型。 货币时间价值(Time Value of Money) 单利法(Method of Simple Interest) 货币时间价值是指在运用过程中,随着时间的推移,是 单利法是计算利息的一种方法。无论时间长短,只按本 可以增殖的,即把资金存入银行或购买债券可以生息,把资 金计算,其所生利息不再加入本金重复计算利息。按单利法 金投资于某项事业可以获得利润。所以严格地说,货币时间 计算得到的未来期限末的本利和,称为单利终值。单利终值 价值应叫资本(资金)的时间价值,它是以一定的经济活动 与本金之差称为单利息。其计算公式是: 所产生的增殖或利润来表达的。货币的时间价值量取决于 F=P(1+i) 时间量和利率两个基本因素,也就是同样的货币量,使用时 I=Pit 间越长,利率越高,则资金的时间价值越大:反之,则越 式中,F一本利和,即单利终值: 小。 P一本金: 时间和利率对货币价值的影响程度,可用因素分析法 一利率: 计算。 1一资金占用时间: 例如,某人有现金10000元,准备存入银行生利,有两个 —单利息。 方案供选择: i和t的规定必须一致。若i是年利率,则t以年计:若i A.资金10000元存入银行,利率为10%,2年期的本利和是月利率,则t以月计:若i是日利率,则t以日计。 为12100元: 由于资金占用时间的计算方法不同,单利法又可分为普 B.资金10000元存入银行,利率为12%,3年期的本利和 通单利法和准确单利法。 为14049元。 普通单利法(Method of Ordinary Simple Interest)资金占 两者差异是:14049-12100=1949(元) 用时间,每月均按30天计算,计息时间t是近似数,其计算方 因素分析: 法是: 方案A的本利和:10000×(1+10%)2=12100(元) 若t以日计,则计息天数: 时间仍为两年,利率由10%提高到12%,则本利和为: t=360×年数+30×月数+尾数天数 10000×(1+12%)2=12544(元) 若t以月计,则计息月数: 即由于利率的不同,本利和存在444元差异。 t=近似天数÷30 方案B的本利和:10000×(1+12%)3=14049(元) 若1以年计,则计息年数: 即利率不变,时间由两年增加到3年,差额为: 1=近似天数÷360 14049-12544=1505(元) 准确单利法(Method of Accurate Simple Interest)资金占 即由于存款期的不同,本利和存在1505元差异。 用时间,按日历中所经历的实际天数计算,其计算方法是: 分析结果说明A,B两个方案的本利和的差异为1949元, 若t以日计,则: 其中利率由10%提高到12%,影响444元:存款期由两年增加 【=实际天数 到三年,影响1505元。 若t以年计,则:

4第一篇金融定量分析方法 t=平年实际天数÷365(或闰年实际天数÷366) 由上式可看出,总有: 单贴现法(Method of Simple Discount) F(1-t)=1+ 在近代工商业交易往来中,通常是使用标明面值和到期日 i>r 的票据。票据未到期不能兑付。如果持票人需要现金,可持票 据向银行兑取现款。银行按市场利率扣除自兑现日至到期日 单利债务分偿法(Separate Redemption Method of 的利息后,将票面余额付给持票人。票据到期后,银行向最初发 Debt with Simple Interest) 票的债务人或背书人兑取现款,这就是所谓贴现。简言之,贴现 金融债务在债务期间内分若干次清偿的方法称为债务分 就是把票据到期日时的价值,折算成贴现日的价值。 偿。如果采用单利法计息,则称为单利债务分偿法。 贴现又可分为单贴现与复贴现,单贴现用单利法计算,复 常用的单利分偿法有单利普通债务分偿法和先息后 贴现用复利法计算。单贴现法又分为单利率贴现法和单贴现 本法。 率贴现法。 单利普通债务分偿法(Ordinary Separate Redemption Meth- 单利率贴现法(Simple Interest Rate Discount Method)此 od of Debt with Simple Interest)把期初贷款额和每次清偿金 法是最简单,应用也较为广泛的贴现方法。其计算公式是: 额采用普通单利法折算到清账日时的金额,清账日时的欠款 F 额就是债务累计值与债务清偿累计金额的差。例如,1997年3 P=T+i 月5日某企业以年利率10%向银行贷款300万元,同年9月 I Pit 15日还款100万元,又于同年11月28日还款130万元,清账 式中,P—贴现额; 日为1997年12月30日。如果采用单利普通债务分偿法,则 F—票面金额: 贷款300万元的终值是: —一单利率: t一计息期数; 300×1+10%×)=324.5833(万元) 一贴现息: 第一次偿债100万元的终值是: 1 1+it 一单利率贴现因子。 10×1+10%×)=102.9167(万元) 单贴现率贴现法(Simple Discount Rate Discount Method) 第二次偿债130万元的终值是: 单利率贴现法是以本利和的现值为准,而单贴现率贴现法则 130×1+10%×)=151.1566(万元) 是以到期值为准。此法相当于银行借给持票人与票据到期值 偿还贷款额终值累计金额是: 相等的本金,依此数额计算利息,并先扣除,所以兑现额是到期 102.9167+131.1556=234.0723(万元) 值与贴现息之差。银行常用此贴现方法。其计算公式是: 清账日企业欠银行贷款金额是: I=Frt 324.5833-234.0723=90.5110(万元) P F-I=F 1-rt) 式中,P一贴现额; 先息后本法(First-interest and Last-principal Method) 每次分偿债务时,首先要计算出所欠余额到该时刻所生的 F一票面金额; 利息,然后,从该次偿还额中首先扣除利息,多余部分属于还 一单贴现率; 本额,再从前次欠款余额中减去这部分还本额,其差额就是 t一计息期数: 一贴现息。 下期的欠款余额。如果本次偿还额不足以抵偿该期利息,账 目上不做还本付息计算,只是把这笔还款记下来,待以后的 偿还额与其相加,其总和超过前几次利息时,再一并按上法 单贴现法等值率(Equivalence Rate of Simple Dis- 处理。直到债务到期清偿时再做最后一次的付息还本结算。 count Method)】 仍以单利普通债务分偿法中的例子说明如下: 设票据的到期值为F,贴现日至到期日的计息期数为t。 1997年9月15日负债余额是: 如果分别用单利率贴现法和单贴现率贴现法求得的贴现额都 是P,那么这时单利率i和单贴现率r对贴现息来说是等价的, 30×(1+10%×8) -100=215.8333(万元) 我们称这种率值等价关系为单贴现法等值率。 1997年11月28日负债余额是: 其数学表达式是: 215.8333×(1+10%×)-130=02099(万元) i1-t 1997年12月30日结账时负债余额是: r二1+t 90.2099×(1+10%×360】 321 =91.0118(万元)

第1章货币时间价值方法5 复利法(Compound Interest Method) 现为收入:运用或支付现金称为现金流出(Cash Outflow),表现 复利法是计算利息的一种方法。银行按规定,经过一定 为成本。(3)现金流的时间性:不同时间的现金流具有不同的 时期结息一次,结息后即将利息并入本金再计利息,即所谓 意义,因为现金流具有时间价值。在分析现金流时,我们必须综 “利上加利”的计算方法。此法也可应用于企业投资效益分 合地考虑这三方面的特征。 析,企业投资一定数额本金,创造纯收,又被再次投入,扩大生 一个项目所带来的现金流往往是一系列的,通常把这些 产,又能获得一定的收益,如此循环,不断提高经济效益。按 现金流的全体看成一个集合,称之为现金流序列(Cash Flow 复利法计算得到的未来期限末的本利和,称为复利终值。复 Stream)。在投资之前,项目所产生的现金流序列可能是确定 利终值与本金之差,称为复利息。复利法有间歇复利法和连的,但大多数情况下是不确定的,这种不确定性即是风险。风 续复利法两种。 险是人们所关注的中心问题之一。 间歇复利法(Intermittent Compound Interest Method)通 现金流序列的表示方法一般有两种:列表法和图示法。 常以年、季、月、日为计息期,到期就立即结息并将利息并入本 列表法是将所有不同时期的现金流用一张表清晰地描述出 金再计利息的计息方法。其计算公式是: 来。图示法是在一条直线上标上不同的时点及其现金流,从 F=P(1+i)' 而直观地进行描述。如图1-1-1所示: 1=F-P=P[(1+i)'-1] 01234+*+…1-1t 式中,F一复利终值: 11 P一本金; CF1 CF2 CF3 CF4 CFCF 一复利率; 一计息期数; 图1-1-1现金流图示法 —复利息: 0一表示0期,即现期(Present); (1+i)一复利终值系数。 1,2,表示第1,2,…期: 若本金是P,年利率是i,每年结算m次,则t年后的本利 1一表示未来第t期: 和是: CF,一表示t期的现金流。 F=P1+) 例如,有两个投资机会,分别表示为投资A和投资B,其现 金流序列用列表法表示如表1-1-1。 连续复利法(Continuous Compound Interest Method)资金 表1-1-1 两个投资机会的现金流 每时每刻都生息,随时将利息并入本金再计利息的计息方法 称为连续复利法。其计算公式是: A投资 B投资 F=Pe“ 时间 现金流量 时间 现金流量 I=F-P=P(e“-1) 1 $500 1 $900 600 式中,F—连续复利终值: 2 600 3 700 3 500 P一本金: 4 800 4 400 e一自然对数的底数,是无理数,e=2.71828: 总计 $2600 总计 $2400 一复利率: —一计息期数: 用图示法表示为图1-1-2。 一复利息。 A投资 注:i和t的规定必须一致,即:若i是年利率,则t以年计: 1 2 3 4 总计 若i是月利率,则t以月计:若i是日利率,则t以日计。在经 济活动中,资金每时每刻在运动,从理论上讲应采用连续复利 $500 600 700 800 $2600 法计息,但在实际的经济活动中,都是采用间歇式复利法计 B投资 息。例如,我国现行的企业存款多为按季计算复利,居民活期 储蓄存款按年计算复利。因此,平时所说的复利法,通常是指 0 1 2 3 总计 间歇式复利法。 $900 600 500 400$2400 现金流(Cash Flow) 图1-1-2两个投资机会的现金流 现金流是一个投资项目(或一个企业)在一定时期内所产 生的现金及其运用。它具有3个特征:(1)流量的规模或大小。 时间价值分析模型(Time Value Analytical Model) (2)现金流的方向性:收到现金称为现金流入(Cash Inflow),表 对于现金流来说,经济意义上的价值和会计意义上的利

6第一篇金融定量分析方法 润是不同的前者必须考虑时间价值,即时间是具有价值的, 表中不仅到出了每期的现值,还到出了各期现值的加总, 现期的100元与1年后的100元是不相同的,考虑到时间价 从而得到每个项目的现值。用公式表示为: 值,前者的价值高于后者的价值。时间价值从经济学上体现 了消费者的时间偏好。一般地认为,对于消费者,同一商品现 Pv=∑CE,·(1+k,) (2) 期消费所产生的效用比未来消费所产生的效用要高,因此,要 式中,n一一共有n期现金流。 放弃现期的消费,必须在未来用更多的量作为补偿,两者的比 通过表1-1-2可见,投资A的现值为82022.75,投资B 即是时间偏好。从金融理论角度来看,时间价值体现了投资 的现值为s1962.92。所以在折现率为10%时,投资A优于投 机会成本(Oppotuninty Cost)。现期的100元可以投资于无风 资B。 险资产(Risk一Free Asset),得到一个合适的增长率一无风 当然,在对项目进行评价时还要考虑其成本(即0期的现 险利率(它应与社会平均时间偏好率相等),从而1年后的总 金流出),一般表示为C,即C=-CF。,在上例中假定成本为 值将大于100元。因此,在对现金流进行评价时应把所有的现 $1200,即CF。=-s1200(负号表示流出),则成本C= 金流以适当的折现率将其换算成与现期等价的价值,即现值 S1200。将A,B的现值减去成本即可得到净现值(Net Pres- (Present Value)。 ent Value)简记为NPV: 现金流的现值计算主要用到数学中级数求和知识。一般 NPV ∑CF,(1+k)-C (3A) 用CF?表示t期末的现金流,用PV表示现值。如果从现期(O 期)到:期末的投资机会成本表示为折现率K则CF,的现值 = cF,1+,) (3B) 0 式中,k。=0,CF。=-C。用公式(3)计算得到A的NPV为 s822.75,B的NPV为s762.92. PV CF 与现值相对应的是未来值或期终值(Future Value or Ter~ 图1-1-3现值计算 minal Value)的概念,表示为FV。未来值是指现期的资金按适 可用下列公式计算如图1-1-3所示: 当的利率,(从数值上应等于前述的折现率)储蓄到:期末的 本利和,即: CF, PV=- (1A) (1+k,) FV PV(1 +rt) (4) 类似地,在10%的利率下对前述例子进行计算可得表1-1-3: =CF,·(1+k) (1B) 说明:计算表1-1-2中未来值时所用到的公式不是(4) 式中,(1+k,)‘—再投资产生复利 而是: k,一从0到1期中每一期的折现率。 FV CF,(1+r)" (1B)中的CF,说明CF是时间1的函数。显然,随着1的 表1-1-3的结果与表1-1-2的结果是等效的,但在对 变化,一般缸也发生变化。为了简化问题,我们先来计算k,为 资产现金流进行评价时更多地是用计算现值来进行。 常数时的情形。仍以计算“现金流”的例子为例,若,=10%, 表1-1-3 利率为10%的未来值 便可算出各个现金流所对应的现值:对于投资A,第一期现金 流的现值为: 投资A 投资B 500 时间 现金流量 FV 时间 现金流量 FV (1+0.1)=454.55 PV 1 $500 665.5 1 $900 1197.9 第二期现金流的现值为: 2 600 726 2 600 726 600 PV = (1+0.1)F=495.87 3 700 770 3 500 550 4 800 800 4 400 400 将所有的现值计算出来列表如表1-1-2。 总计 $2600 82961.5 总计 $2400 82873.9 表1-1-2 以10%折现的现金流 参见“单利法”“单贴现法”“复利法”等。 投资A 投资B 时间 现金流量 现值 时间 现金流量 现值 时间价值的灵敏性分析(Sensitive Analysis for Time 1 8500 454.55 $900 818.18 Value) 2 600 495.87 2 600 495.87 在用时间价值模型公式(2)计算现值,用公式(3)计算净 3 700 525.92 3 500 375.66 现值和用公式(4)计算未来值时,时间价值体现在折现率k,和 4 800 546.41 400 273.21 利率,上。实际上,当时间价值发生变化时,相应的值也发生 总计 s2600 $2022.75 总计 82400 $1962.92 变化,而且有时对时间价值变化的反应是很灵敏的。下面对
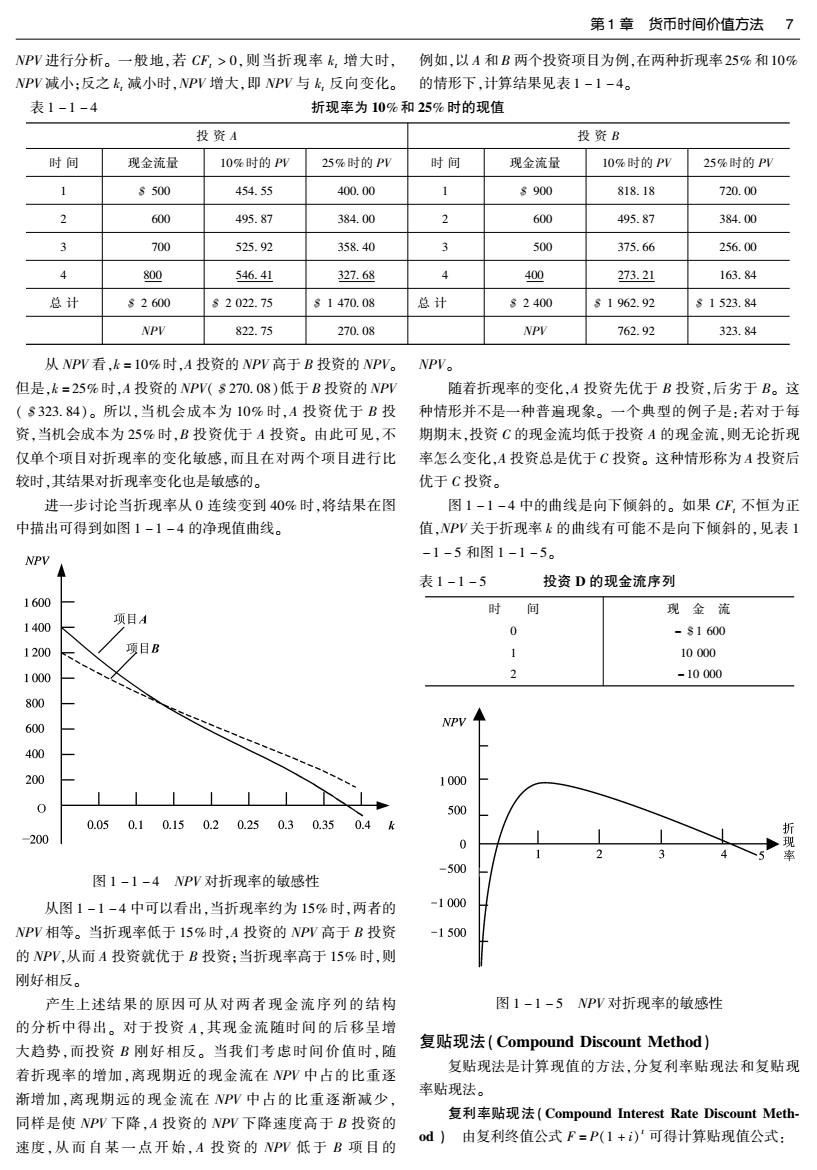
第1章货币时间价值方法7 NPV进行分析。一般地,若CF,>0,则当折现率k,增大时, 例如,以A和B两个投资项目为例,在两种折现率25%和10% NPV减小:反之k,减小时,NPV增大,即NPV与k,反向变化。 的情形下,计算结果见表1-1-4。 表1-1-4 折现率为10%和25%时的现值 投资A 投资B 时间 现金流量 10%时的PV 25%时的PV 时间 现金流量 10%时的PV 25%时的PV s500 454.55 400.00 1 8900 818.18 720.00 2 600 495.87 384.00 2 600 495.87 384.00 3 700 525.92 358.40 3 500 375.66 256.00 4 800 546.41 327.68 4 400 273.21 163.84 总计 82600 S2022.75 s1470.08 总计 82400 s1962.92 81523.84 NPV 822.75 270.08 NPV 762.92 323.84 从NPV看,k=10%时,A投资的NPV高于B投资的NPV。 NP。 但是,k=25%时,A投资的NPV(s270.08)低于B投资的NPV 随着折现率的变化,A投资先优于B投资,后劣于B。这 (S323.84)。所以,当机会成本为10%时,A投资优于B投 种情形并不是一种普遍现象。一个典型的例子是:若对于每 资,当机会成本为25%时,B投资优于A投资。由此可见,不 期期末,投资C的现金流均低于投资A的现金流,则无论折现 仅单个项目对折现率的变化敏感,而且在对两个项目进行比 率怎么变化,A投资总是优于C投资。这种情形称为A投资后 较时,其结果对折现率变化也是敏感的。 优于C投资。 进一步讨论当折现率从0连续变到40%时,将结果在图 图1-1-4中的曲线是向下倾斜的。如果CF,不恒为正 中描出可得到如图1-1-4的净现值曲线。 值,NPV关于折现率k的曲线有可能不是向下倾斜的,见表1 -1-5和图1-1-5。 NPV 表1-1-5 投资D的现金流序列 1600 时 间 现金流 项目A 1400 0 -s1600 1200 项目B 1 10000 1000 2 -10000 800 600 NPV 400 200 1000 0 500 0.050.10.150.20.250.30.35 0.4k 折 200 0 -500 图1-1-4NPV对折现率的敏感性 从图1-1-4中可以看出,当折现率约为15%时,两者的 -1000 NPV相等。当折现率低于15%时,A投资的NPV高于B投资 -1500 的NPV,从而A投资就优于B投资:当折现率高于15%时,则 刚好相反。 产生上述结果的原因可从对两者现金流序列的结构 图1-1-5NPV对折现率的敏感性 的分析中得出。对于投资A,其现金流随时间的后移呈增 大趋势,而投资B刚好相反。当我们考虑时间价值时,随 复贴现法(Compound Discount Method)】 着折现率的增加,离现期近的现金流在NPV中占的比重逐 复贴现法是计算现值的方法,分复利率贴现法和复贴现 渐增加,离现期远的现金流在NPV中占的比重逐渐减少, 率贴现法。 同样是使NPV下降,A投资的NPV下降速度高于B投资的 复利率贴现法(Compound Interest Rate Discount Meth- od)由复利终值公式F=P(1+)'可得计算贴现值公式: 速度,从而自某一点开始,A投资的NPV低于B项目的

8第一篇金融定量分析方法 P=- F 式中,P一贴现额; (1+i) F一票面金额: 式中,P—贴现额: —复贴现率: F—票面金额: t一计息期数。 一复利率: 显然,分别用以上两种方法求得的票据的贴现额相等时,定有 t一计息期数: r=io 1 一复利贴现系数。 (1+) 复利计息期数的计算(Interest Period of Compound 复贴现率贴现法(Discount Method of Compound Discount Rate)以到期值为准,以此数额用复利法计息,并先扣除的 Interest) 方法为复贴现率贴现法。其计算公式是: 如果已知复利终值F,现值P,利率i,则可由复利终值公 P=F(1-r)' 式F=P(1+i)'得到计算期数的公式: 式中,P一贴现额: IgF-IgP 1= 1g(1+i) F一票面金额; 例如,终值F=1000,现值P=900,月利率i=10%c,每月 一复贴现率; 复利一次,则计息期数为: t一计息期数。 1=000-1900=10.5886个月(即10个月18天) 1g(1+10%c) 复贴现法等值率(Equivalence Rate of Compound Discount Method)】 计息期数为非整数的复利终值和现值(Compound 设票据的到期值为F,贴现日至到期日的计息期数为t。 Final and Present Value of Non-integral Interest Pe- 如果分别用复利率贴现法和复贴现率贴现法求得的贴现额都 riod) 是P,那么这时的复利率i和复贴现率,对贴现息来说是等价 当计息期数t为非整数时,复利终值公式F=P(1+i)'和 的,我们称这种率值等价关系为复贴现法等值率,其数学表达 式是: 复利现值公式P= F1十)也是适用的。这种计算计息期数为 i二1-r 非整数的终值与现值的方法称为终值与现值的准确算法。例 如,若年利率为10%,每年复利一次,则两2零3个月后1000 i r二1+i 元的终值是: 由上式可看出,总有: F=1000×(1+10%)25=1239.18(元) 2年零3个月前的现值是: F(1-r)'=(1+i订 1000 P=0+10%25=806.9(元) i>r 实际上,准确法并不常用。常用的方法是复利法计算最接 连续复贴现法(Continuous and Compound Discount 近的整数计息期部分,再用单利法计算不足一个计息期以内 的部分利息。这种计算计息期数为非整数的终值与现值的方 Method) 法称为终值与现值的近似算法或实用算法。其计算公式是: 计算现值的方法,分连续复利率贴现法和连续复贴现率 贴现法。 F=P(1+i)0[1+(t-[t])] 连续复利率贴现法(Continuous and Compound Interest Rate F P=a+i1+(0+1-) Discount Method)由连续复利终值公式F=Pe可得连续复利 式中,F一终值: 率贴现法计算贴现值公式: P一贴现值: P=Fe-h 一利率: 连续复贴现率贴现法(Continuous and Compound Discount —一非整数计息期数; Rate Discount Method)由复贴现率贴现法计算现值公式P= [t]一1的整数部分: F(1-r)'可知,若每年复贴现m次,则贴现值为: t-[]一t的正纯小数部分,0<t-[]<1。 P=-) 用实用算法可算得上例中,两年零三个月后1000元的终 当每年贴现次数m→∞时,则贴现值为: 值是: F=1000×(1+10%)2×(1+0.25×10%)=1240.25(元) P-limp-im()=Fe 2年零3个月前1000元的现值是:

第1章货币时间价值方法9 (1+10%)×(1+0.75×10%)=807.66(元) 1000 P= 称为年金额。自第一次支付期间开始到最后一次支付期间终 了的时期,称为年金时期。每期末支付的年金,称为普通年 金,或期末付年金。每期初支付的年金,称为期初年金。 特殊现金流评价(Specific Cash Flow Evaluation) 我们在时间价值分析模型中得到了一般现金流的评价 年金终值(Final Value of Annuity)】 计算方法。为了便于使用,人们编制了在不同折现率下1个 即各期支付的年金在年金时期终了时的终值之和,称为 单位期末值所对应的现值表,即现值系数表。尽管如此,当 年金终值。有单利年金终值和复利年金终值两种情况。 较大时,人工计算仍然十分麻烦。因此,便引出了年金的概 单利年金终值(Simple Interest Final Value of Annuity) 念。 若每期发生年金额为A,每期利率为i,共1期,以单利计息,则 所谓年金(Annuity)是指满足下列4个条件的现金流序列: 各期支付的年金在年金时期终了时的本利和总额称为单利年 1.现金流量大小固定不变,时间间隔固定(一般指每年支 金终值。单利年金终值又可分为单利普通年金终值和单利期 付一次现金): 初年金终值两种情况: 2.支付期限为有限期: (1)单利普通年金终值。每期年金的本利和如表1-1-6 3.从第一期末开始支付,每期期末支付现金: 所示。 4.对所有的现金流,其折现率相同。 表中最后一行是各期年金终值,其和就是单利普通年金 根据以上条件,用等比级数求和公式不难算出期限为n 终值: 期,折现率为k,现金流量为CF(因为CF,为常数,故省去t)的 F=A+A(1+i)+…+A[1+(t-2)i]+A[1+(t-1)i] 年金现值,记为PVA: PVA CF.I-(1+k) =4[1+专(t-1)i] (1) k 表1-1-6 相应地,在利率为r的条件下,年金的未来值(FVA)可用 期 数 1 2 公式(2)计算: FTA=CF.1+)"-1 每期末年金 A A (2) t期末终值 4[1+(t-1)]4[1+(t-2)i] A(1+i) 最后,考虑一个特殊情形:某项投资预期有无限期的现金 流,而且其现金流以一固定增长率g增长,现金流的产生时间 (2)单利期初年金终值。每期年金的本利和如表1-1-7 间隔固定,所有的现金流用同一折现因子进行折现,则由无穷 所示。 等比级数求和公式可求得其现值为: 表中最后一行是各期年金终值,其和就是单利期初年金 WV.C (3) 终值: F=A(1+i)+A(1+2i)+…+A[1+(t-1)]+A(1+i) 这就是所谓的固定增长模型(The Constant Growth Mod- l)。因为由第一期现金流CF,和增长率g可推得所有其他各 =41++1)月 期的现金流,因此(3)中只出现CF,。 表1-1-7 在公式(3)中,当g为零时,即是“零增长模型”(The Zero 乡 华 2 Growth Model)。当g取零值时,相应的现金流是终身年金 (Perpetual Annuity),此时,现值可由(l)式取n趋于无穷大或 每期初年金 A A A 由(3)式取g=0相应地得出: t期末终值 A(1-t) M[1+(t-1)i] 4(1+2)M(1+i) Py =CF k (4) 复利年金终值(Compound Interest Final Value of Annuity) 这个公式虽然十分简单,但它具有深刻的经济意义。它 若每期发生年金额为A,每期利率为i,共t期,以复利计息,则 对评价诸如固定红利的优先股之类的终身年金十分有用,同 各期支付的年金在年金时期终了时的本利和总额称为复利年 时也广泛地用于对永久性固定附息息票债券的定价。 金终值。又可分为复利普通年金终值和复利期初年金终值两 种情况。 年金(Annuity) 1.复利普通年金终值。每期年金的本利和如表1-1-8 在一定时期,每间隔相等时间支付的金额,称为年金。例 所示。 如每月支付的房租,水电费、债券利息、股息、购货的分期付款 表中最后一行是各期年金终值,其和就是复利普通年金 等,都可称为年金。年金一般按固定利率计算利息。相邻两 终值: 个支付日的期间,称为支付期间。每一支付期间支付的金额, F=A(1+i)-1+A(1+i)-2+…+A(1+i)+A

10 第一篇 金融定量分析方法 =41+-1 表1-1-10 i 乡 数 2 t-1 表1-1-8 每期末年金 A A A A 乡 数 -1 各期年金 A A A 现值 1+i 1+2i 1+(t-1)i 1+ 每期末年金 A A +… A 2.单利期初年金现值。各期年金的现值如表1-1-11 :期末终值 A(1+i)- A(1+i)-2 A(1+i) 所示。 常把上式中1+'-山的称为年金终值系数,亦称等额分 表中最后一行是各期年金现值,其和就是单利期初年金 i 现值: 付本利和系数。由复利普通年金终值计算公式F=A A■ A (1+i)‘-1可得如下公式: i 表1-1-11 A=F)-1 i 期 数 2 4-1 此式的经济意义是,假如要在t年末筹集一笔款F,若 每期初年金 A A A A 利率为i,则按复利计算时每年应等额存入银行的款额应为 各期年金 A A A 现 1+i 1+(t-2)i 1+(t-1)i 4。式中的1+一称为年金储存系数,亦称资金存储系 复利年金现值(Compound Interest Present Value of Annui- 数。 y)若每期发生的年金额为A,每期利率为i,共t期,复利计 2.复利期初年金终值。每年年金的本利和如表1-1-9 息,则各期支付的年金在年金时期初的现值之和称为复利年 所示。 金现值。复利年金现值又可分为复利普通年金现值和复利期 表中最后一行是各期年金终值,其和就是复利期初年金 初年金现值两种情况。 终值: 1.复利普通年金现值。各期年金现值如表1-1-12 F=A(1+i)”+A(1+i)-1+…+A(1+i)2+A(1+i) 所示。 =A(1+)1+i)-1 表中最后一行是各期年金现值,其和就是复利普通年金 现值: 表1-1-9 A A A A 期 数 2 P=++++…+1+)++) ++4+ =A1-1+) 每期初年金 A i 1期末终值 A(1+i)t A(1+i)t-1 1(1+i)2A(1+i) 表1-1-12 期 数 1 2 t-1 年金现值(Present Value of Annuity)】 每期末年金 A 年金现值即各期支付的年金在年金时期初的现值之和。 A A A 各期年金现值 分为单利年金现值和复利年金现值两种情况。 1+i (1+i) (1+)可 (1+i) 单利年金现值(Simple Interest Present Value of Annuity) 若每期发生年金额为A,每期利率为i,共1期,单利计息,则各 常把上式中】-(1+)二的称为年金现值系数,亦称等额 期支付的年金在年金时期初的现值之和,称为单利年金现值。 支付现值系数。 单利年金现值可分为单利普通年金现值和单利期初年金现值 两种情况。 由复利普通年金现值计算公式P=AL-(1+),得投资 i 1.单利普通年金现值。各期年金的现值如表1-1-10 回收值公式: 所示。 i 表中最后一行是各期年金现值,其和就是单利普通年金 A=P1-(1+i) 现值: 此式的经济意义是:假如为实施某技术方案需向银行贷 P=+中2+…+14d丽+=名 A A 款P,利率i,按协议要在t年等额偿还,则每年应偿还额为A。 白1+m 投资回收值公式中的, -(1+)称为资金回收系数,亦称资 金还原系数

第1章货币时间价值方法11 2.复利期初年金现值。各期年金现值如表1-1-13所示。 求年金支付期数t。根据复利普通年金终值公式F=A 表中最后一行是各期年金现值,其和就是复利期初现值: 1+-或复利普通年金现值公式P=A-口+),利用 i A A A A i P=A+++++…+0+0+1+)四 对数,即可求得年金支付期数t和年金期限。一般地,由F或 =A(1+)1-(1+) P,I求得的支付期:不是整数。因此,需要调整最后一次支付 的年金金额,以使总和相等。常用下面两种方法调整: 表1-1-13 1.在最后一笔年金金额上加上一定数量的金额,使得各 期 数 0,。+ t-1 次支付的年金总和恰好等于年金终值F或现值P。 2.在最后一次正规支付之后,再求解出一笔较少的收尾 每期初年金 A A …… A 付款,并让它另占用一个新的计息期支付。在新增加的这个 A A A 各期年金现值 A (1+i) 0+)1+) 计息期里,因为原来已积累的年金终值能够再生息且此利息 总是超过结算金额,所以设想的那笔较少收尾付款就不必支 付了。 复利普通年金利率的计算(Compound Interest Ordi- nary Annuity Rate) 变额年金(Variable Annuity) 在许多投资活动中,真实利率往往是隐蔽的。为了比较 每期发生的年金不是常量,这样的年金称为变额年金。企 几个不同的投资方案,很有必要确定每个投资方案的实际利 业采用的分期分批不等额投资方式,即属变额年金。年金额 率水平,并据此做出投资决策。 的变动可分为下面3种情形: 在复利普通年金终值公式F=AL+'-上中,常要由F、 1.等差变动。每期发生的年金分别是A,A+d、A+2d, i :当d>0时,年金是递增的:当d<0时,年金是递减的。此 A和1来确定利率i,显然,用解高次方程F=A①+)'-山的 时普通年金复利现值和终值的计算方法是: 方法计算利率1是较为困难的,通常用线性插值法求出它的近 似解。具体步骤如下: ++0++ (1+) 1.选择适当的利率并由年金A进行试算,如果试算得到 ++4*…*4小 A 的年金终值小于实际终值F且差额较大,就用高利率再试算, *4+*+别 2d 3d 直到试算出一个小于且接近于实际终值F的终值F,把确定 F,的利率记为i1 2.再选择比i,大的利率并由年金A进行试算,如果试算 设 n=+a+a可*…*a时 A A 得到的年金终值大于实际终值且差额较大,就降低利率再试 算,直到试算出一个大于且接近于实际终值F的终值F:,把确 则B=A1-(1+i) 定F2的利率记为2: 设+华粉+分++名,提 d 2d 3d 3.把试算得到的马F,F代入线性插值公式: (1+i) 于 i=i*F+3(-4) 1+04+a+a++名:鼎 2d 求出利率i。 (1+i)回 为了使求得的利率i较为准确,常要求i2-i小于1%。 上面两式相减,得: 例如,若每月末存款250元,连续16个月,要使终值达到 识=4+a中+a可+…+ū++ d d d_(t-1)d 5000元时,则月利率应是多少?按以上方法可求得: i1=2.8%时,F,=4960.46 =d1-(1+)--1)4 (1+i) i2=3.0%时,F2=5039.22 则月利率为: 从而 B=d-*i)-d-1 “i(1+i) 4960.46 i=28%+4960.46+5039.22×(3.0%-28%) 所以 P=P +P2 =2.9% =A-1+出+a-+)-d,- i (1+i) 年金期限的计算(Calculation of Annuity Term) 有时要由年金终值F或年金现值P、年金金额A、利率i来 -++d+)