
第六篇 保险实务定量分析 保险(Insurance)一词是在17世纪从英国传入中国的。英女王伊丽 沙白在15世纪颁布的诏书中对保险作如下表述:“保险是将损害由少数 人的重负担变成多数人的轻负担。”这一古典定义高度概括了保险含义, 至今仍为各国保险业界所认同。 《中华人民共和国保险法》称保险“是指投保人根据合同约定,向保 险人支付保险费,保险人对于合同约定的可能发生的事故因其发生所造 成的财产损失承担赔偿保险金责任,或者当被保险人死亡、伤残、疾病或 者达到合同约定的年龄、期限时承担给付保险金责任的商业保险行为”。 保险一般可以划分为人身保险和非人身保险两大类。 保险公司是非银行金融机构,保险公司在某些方面具有与银行金融 机构相似的特点,特别是保险公司也具有融资的功能。但是,作为提供保 险产品服务的金融机构,保险公司的业务活动及经营管理又具有其特殊 性。本篇共收录可定量分析的保险词条509个。分为财产保险业务、人 寿保险业务、医疗保险业务、再保险业务、社会保险业务和保险公司经营 管理等六章来讨论

第1章财产保险业务1149 第1章 财产保险业务 财产保险(Property Insurance)是以被保险人财产及其有关利益作为保险标的的保险。或以造成财产经 济损失的赔偿责任作为标的的保险。 财产保险就其范围而言,可作狭义和广义之解释。狭义的财产保险,仅指物质财产作为保险标的的保 险。它包括处于相对静止状态下的财产物资,如楼宇、地产等,和处于流通过程中的财产物资,如汽车、船 舶、飞行器等。广义财产保险标的不仅包括物质财产,还包括与物质财产有关的经济利益,如预期利润、运 费、信用等,以及损害赔偿责任,如信用责任、公众责任、产品责任、职业责任等。我国《中华人民共和国财产 保险合同条例》第二条规定:“本条例所指的财产保险,包括财产保险、农业保险、责任保险、保证保险、信用 保险等以财产或利益为保险标的的各种保险。”可见,我国使用的财产保险概念,是指广义的财产保险,由于 保险业务包括财产保险和人身保险两大类别,因而习惯上人们又把财产保险视作人身保险之外的一切保险 业务的总和。 本章从个体风险入手,首先展开了一系列风险模型分析,通过分析出险频率与损失幅度的分布,研究出 险次数与每项损失大小的随机过程,之后分析损失分布状况以及损失分布与赔款的相互关系等:接下去进 行纯保贵和赔款准备金的精算分析:最后,对火险、机动车保险、水险、运输险、建工险和雇主责任险等具体 风险进行实务性分析。 个体风险(Individual Risk) 风险是以其变异性的大小进行度量的,因此度量风险水 方法分别为]和[X],侧风险集合的总损失为宫了 平的两个常用指标就是风险的方差和变异系数。方差反映 均值为E[立x]方差为@[立x]在没有保险的情况 了风险的绝对量,而变异系数反映了风险的相对水平。 下,保险人和被保险人所承担的风险如表6-1-3所示。 令X表示个体风险的随机损失,其均值为E[X],方差为 表6-1-3 没有保险时风险的转移情况 Va㎡[X]。在没有保险的情况下,保险人和被保险人所承担的 风险情况如表6-1-1所示。 被保险人承担的部分 保险人承担的部分 表6-1-1 没有保险时个体风险的转移情况 随机损失 0 被保险人承担的部分 保险人承担的部分 期望损失 =含 0 随机损失 0 期望损失 E[X] 0 方 差 方 Var[X] 0 如果风险集合中的所有个体风险都购买了全额保险,则 如果被保险人通过支付固定的保费E[X]将随机损失X 保险人和被保险人之间的关系如表6-1-4所示。 转移给保险人(这里暂且忽略附加保费和利率等因素),则保 表6-1-4 购买保险时风险的转移情况 险人和被保险人所承担的风险情况如表6-1-2所示。 被保险人承担的部分 保险人承担的部分 表6-1-2 购买保险时个体风险的转移情况 随机损失 2x,-2E[x] 被保险人承担的部分 保险人承担的部分 随机损失 E[X] X一E[X] 期望损失 EX)=EX) 0 期望损失 E[X] 0 方差 0 Var[X] 差 >Var[X.] 从表6-1-2可以看出,被保险人通过支付固定的保费 当被保险人只是将其随机损失的一部分转移给保险人 E[X],将其随机损失X的变异性Vr[X]全部转移给了保险人。 时,情况会变得更加复杂。 风险集合(Risk Aggregaeion) 相对风险(Relative Risk) 对于由n个相互独立的风险所组成的集合,风险的转移也 当许多相互独立且具有相同损失特性的个体风险聚合 可作同样的数学描述。令X为第i个风险的随机损失,均值和 成风险集合时,风险集合的相对变异性要小于个体风险的相

1150第六篇保险实务定量分析 对变异性。在这里,我们通过随机损失的变异系数来反映风 方差分别为E{E[XIr]Ir∈A}和VarE[XIr]Ir∈A。 险的相对变异性。方差反映了风险的绝对量,而变异系数则 其中均值还可进一步化简为 可以反映风险的相对水平。随机损失X的变异系数c:被定 EE[X I r]rEA=E[X I A] (1) 义为标准差War[X丁与均值E[X,]之比,即 上式表明,从风险集合A中随机抽取的个体风险,其期 ce = Narx]a 望损失的期望等于风险集合A的期望损失。由于风险集合A E[X,] (1) 的期望损失E[X丨A]是可以估计的,因此随机个体风险的期 式中u一个体风险X的均值: 望损失的期望E{E[XIt]IT∈A}也是可以估计的。但是, σ2一个体风险X的方差。 个体风险的期望E[XI]是难以估计的,因此随机个体风险 因此,保险的第3条原理也可表述为c[∑X]< 的期望损失的方差Var{E[XIt]Ir∈A}也是难以估计的。 随机个体风险的方差Var[XIr]也是一个随机变量,其 c[X],其中c[∑X]是n个独立风险之和的变异系数, 均值和方差分别为E{Var[XIr]reA}和Var Var[XIr]r cw[X]为第i个风险的变异系数。 eA}。 n个独立同分布随机风险X1,X.之和的均值和方差分别为 E[∑X]=∑E[X]=nE[X]=nu (2)互助性保费(Mutual Premium) 和 如果保险人按照风险集合A的期望损失E[XIA]收取 Var[∑X]=nar[X]=no2 (3) 保险费,那么从总体上看,保费水平是合理的,但对个体风 险而言,平均主义的保费制度可能隐含着相当的不公平性。 从而对于n个具有相同损失特性的独立风险所组成的 个体风险缴纳的合理保费应为E[X!r],因此当其缴纳平 风险集合,其随机损失的变异系数为 均保费E[X丨A]时,他事实上缴纳了互助性保费E[XI c(∑x]:√ar] A]一E[XI]。互助性保费可正可负。若互助性保费大于 E[∑X] 零,则意味着该个体风险缴纳了高于其实际风险水平的保 VnVar[X,] 费:若互助性保费小于零,则说明个体风险在保费上得到了 nE[X (4) 其他投保人的补贴。当个体风险的互助性保费为零时,则 =c] 按照风险集合A的期望损失E[XIA]收取保费,对于这一 个体风险而言是公平的。互助保费的大小反映了被保险人 上式表明,n个独立同分布随机变量之和的变异系数是 之间相互依赖相互补贴的程度,它在稳定保险市场方面有 单个随机变量的变异系数的√n分之一。如果上述n个相互 着十分重要的意义。 独立的随机变量具有不同的分布形式,则可以证明,随机变 量之和的变异系数要小于单个变异系数的某种加权平均数。 风险子集(Risk Sub-analysis) 这一结论对相关程度不高的n个随机变量也是近似成立的。 令S是风险集合A中的风险子集,其损失分布的均值和 因此,对于个具有相近分布形式、相关程度较低的随机变 方差分别为E[XIS]和Vr[XIS]。对于风险子集S,随机 量,上式也能提供一个合理的近似结果。 个体风险的期望损失的期望等于风险子集S的期望损失,即 E{E[XIr]Ir∈A=E[XIS] (1) 由于上式是对随机个体风险的期望损失关于风险子集S 风险集合的损失分布(Lost Distribution of Risk Ag- 求期望,所以结果不等于风险集合A的期望损失,而等于风 gregation)】 险子集S的期望损失。 对于风险集合A,其损失分布的均值和方差可分别表示 如果将风险集合A分解成若干个互不相交的风险子集, 为E[X1A]和Var[XIA]。当风险集合A足够大时,对 每一个个体风险r属于且仅属于一个风险子集,则从风险集 E[XIA]和Var[XIA]可分别估计如下: 合A中随机抽取的个体风险必然对应着一个风险子集。这 可14): (1) 一风险子集也可以看作是随机抽取的,因此其期望损失是一 n 随机变量。若把风险子集的期望损失看作是一个随机变量 axIA利-9_∑g 并对其求期望,则有 (2) n EE[X I S]SEA=E[X IA] (2) 风险子集的期望损失的期望等于风险集合的期望损失。 随机个体风险的损失分布(Lost Distribution of Random Individual Risk) 均值分解(Mean Value Analysis) 如果从风险集合A中随机抽取个体风险,则称r为随机 对于给定的个体风险ī,其期望损失可分解为 个体风险,随机个体风险的期望损失E[X丨]可以看作是一 E[X I]=E[XI A]+(E[X I S]-E[X I A]+ 个随机变量,它有自己的分布函数。这一分布函数的均值和 E[X I ]-E[X I S]) (1)

第1章财产保险业务1151 由此可见,个体风险的期望损失可以表述为下述三项 之和: k(∑X)=E[∑X-(∑x)] 1.风险集合A的期望损失,它确定了风险集合的一般保 =[∑(x-x)] (2) 费水平: 2.风险子集S的期望损失与风险集合A的期望损失之 =∑E[X-E(X)]3 差,它是风险分级所形成的保费差异: =43 3.个体风险的期望损失与风险子集的期望损失之差,这 在E[∑(X-EX)]萨的展开式中,除三次方项E[X- 一部分形成互助性保费。 E(X)]3以外,其余各项的期望值为零。因此n个独立同分 布的随机变量之和的偏度系数为 方差分解(Square Deviation Analysis) 根据条件方差的性质,如果风险集合A由若干个风险子 Y= 集S构成,则风险集合的方差可以分解为 (√/ar[∑x]) Var[XI A]E Var[X I S]I S E A+ (3) Var{E[XIS]IS∈A} (1) o'n n 同样,风险子集的方差可分解为 =Y Var[X I S]=E Var[X I r]l reS+ n VarE[XI r]lr E S (2) 由此可见,个独立同分布的随机变量之和的偏度系数 将(2)式代入“相对风险”式(1)即得 随着的变化呈反方向变化,这一结果与变异系数是相类似 Var[X I A]EE[Var(XI r)I r E S]S E A+ 的。这就说明,风险集合包含的相互独立的个体风险越多, E Var[E(XI r)I r E S]I SE A+ 其损失分布的变异性和非对称性就越小,少数巨灾风险对风 VarE[XI S]I S E A (3) 险集合的影响也就越小,从而对保险公司的经营稳定性就越 =E[Var(XIr)Ir∈A]+EVam[E(XIr)I 有利。 TeS]IS∈A}+VarE[XIS]IS∈A 由此可见,风险集合的方差可分解为下述三部分之和: 同质性保单组合的索赔次数模型(Claim Frequency 1.在风险集合内,个体风险的方差的平均数,它是不可 Model of Homogeneous Policy Combination) 观察的,代表着风险的内在变异性,是保险赖以存在的基础: 所谓同质性是指一个保单组合中每份保单具有相同的 2.在风险集合内,风险子集的方差(即风险子集内不同索赔频率,且各自相互独立。由于个体保单的风险事故属于 个体风险之间的方差)的平均数,它代表着不同个体风险之稀有事件,因此可以假定它的索赔次数过程N()具有如下 间的变异性,在费率结构中没有得到具体体现,因此也造成特性: 互助性保费的变异性; 1.在时间起点,它的索赔次数为零,即N(0)=0。 3.在风险集合内,各个风险子集之间的方差,它代表着 2.在一个足够短的时间区间内,最多只能发生一次索 不同风险子集之间的变异性,费率结构就是这种变异性的具 赔,且发生一次索赔的概率与此时间区间的长度成正比,而 体体现。 发生两次或两次以上索赔的概率是时间长度的高级无穷小 量,即 偏度系数(Biased Exponent) P N(t)=1 At+o(1) 偏度系数反映了损失分布关于均值不对称的程度,它的 P{N(t)=0}=1-At+o(t) (1) 大小受到巨灾风险的影响。随机变量X的偏度系数被定 P{N(t)≥2}=o(t) 义为 3.在两个不相交的时间区间内发生的索赔次数相互独 y=4,/a3 (1) 立,也就是说,N(t)是一平稳独立增量过程,有 式中4,=E[X-E(K)]3一X的三阶中心矩: p{N(t,1+s)=k}=PN(s)= (2) 一X的标准差。 且N(s)与N(t,t+s)相互独立。 对于对称分布(譬如正态分布),偏度系数为零:对于右 可以证明,满足上述三个条件的随机过程为泊松过 偏分布,偏度系数大于零:对于左偏分布,偏度系数小于零。 程,有 非寿险中的大多数损失分布属于右偏型的,即有较长较厚的 P10===0.1,2. (3) 右尾。 如时间长度为1,即令t=1,则上式可简化为 n个独立同分布的随机变量之和的偏度系数是单个随机 变量的偏度系数的1/Wn。这是因为,n个独立同分布的随机 PN=对=行 (4) 变量之和的三阶中心矩为: 由此可见,在一个单位时间内,同质性保单组合的索赔

1152第六篇保险实务定量分析 次数服从参数为入的泊松分布。 保单组合存在某种程度的非同质性。而且方差越是大于均 泊松分布具有如下特性: 值,这种非同质性越严重。这从混合泊松分布的方差与均值 (1)m个相互独立且参数分别为入,的泊松随机变量之 的差项Var(A)很容易看出,因为Var(∧)正是反映保单组 和仍然服从泊松分布,参数为∑A:。但这并不意味着m个 合非同质性程度的结构函数的方差。 相互独立的同质性保单组合的集合的索赔次数仍服从泊松 逆高斯结构函数:泊松一逆高斯模型(Contradictory 分布,因为这个保单集合有可能是非同质的,除非原m个同 Goss Structure Function:Poisson -Contradictory 质性保单组合的索赔频率相等。这里需要强调的是,所谓保 单组合的索赔次数分布是指此保单组合中发生k(k=1,2, Goss Model) 逆高斯分布的密度函数为: …)次索赔的保单数,或者是从此保单组合中随机抽取的一 份保单发生k-1次索赔的概率。 wep)-te-a2] r>0,β>0 (2)泊松分布的均值和方差都等于入,分布参数入的矩 (1) 估计和极大似然估计都是其样本均值X。偏数系数y随着入 相应的泊松一逆高斯分布的概率函数为 的增大逐渐减小,其中y=1/W。 B=脚{-合1+29-} 伽玛结构函数:负二项分布模型(Gamma Structure 月后么浩(9刿 2」 Function Negative Binomial Distribution Model) k=1,23,… (2) 在假定一个保单组合的泊松参数A服从参数为(α,B)的 泊松一逆高斯分布与负二项分布一样也有两个参数,其 伽玛分布的前提下,从此保单组合中随机抽取的任意一份保 均值、方差和偏度系数分别为 单在单位时间内发生k次索赔的概率为 均值μ=r (3) u(A)da (1) 方差G2=r(1+B) (4) 偏度系数y=o[32-2μ+3g二】 (5) =(作+e广( a>0,B>0 其中y就是结构函数一逆高斯分布的均值,方差大于均 此即负二项分布的概率函数。其均值、方差和偏度系数 值的差项yB就是逆高斯分布的方差。 分别为 泊松一逆高斯分布参数的矩估计为 均值u= (2) 子=元 (6) B a=黄-1 (7) 方老d=合1+合) (3) 泊松一逆高斯分布参数r的极大似然估计仍然是?=元 偏度系数y=3{3o2-2μ+2(2-u)2} (4) 参数B的极大似然估计是下述方程的正解 若令x和2分别为样本均值和样本方差,则负二项分布 参数的矩估计为 7@- (8) a=- (5) 式中,T(B)—(1+28)n (6) Te1+k-1B+7ie] k=1,2,… 泊松一逆高斯分布与负二项分布的一个相似性质是对 参数的极大似然估计为B=兰,其中α是下述方程 卷积运算的封闭性,即若N,服从参数为(,,β)的泊松一逆高 的解: 斯分布,且相互独立,则∑N,也服从泊松一逆高斯分布,参 i 含(日++含+)) 数为(立,B)。同样地,若N服从参数为(a,B)的负二项分 由于负二项分布是泊松公布在伽玛分布作为结构函数 时的混合分布,因此它属于混合泊松分布。混合泊松分布的 布,且相互独立,则∑N也服从负二项分布,参数为 一个显著特点是其方差大于均值,即 方差2=Var(A)+E(A) 均值μ=E(∧) 式中,∧一泊松参数,代表结构函数的随机变量。 我们知道,泊松分布的均值等于方差,因此当保单组合 的索赔次数观察分布的样本方差大于其均值时,即可断定此
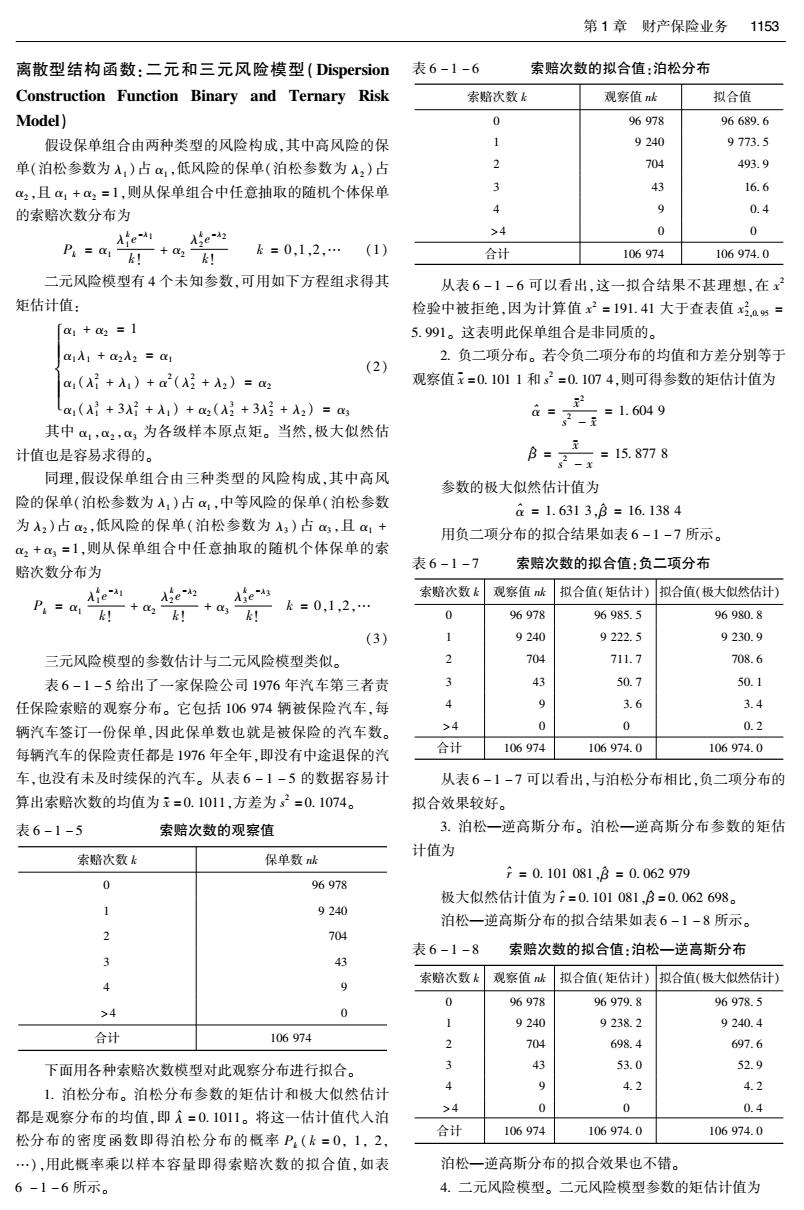
第1章财产保险业务1153 离散型结构函数:二元和三元风险模型(Dispersion 表6-1-6 索赔次数的拟合值:泊松分布 Construction Function Binary and Ternary Risk 索赔次数k 观察值nk 拟合值 Model) 0 96978 96689.6 假设保单组合由两种类型的风险构成,其中高风险的保 1 9240 9773.5 单(泊松参数为入,)占α,低风险的保单(泊松参数为入2)占 2 704 493.9 a2,且α,+a2=1,则从保单组合中任意抽取的随机个体保单 3 为 16.6 的索赔次数分布为 4 9 0.4 >4 0 0 k=0,1,2,…(1) 合计 106974 106974.0 二元风险模型有4个未知参数,可用如下方程组求得其 从表6-1-6可以看出,这一拟合结果不甚理想,在x 矩估计值: 检验中被拒绝,因为计算值x2=191.41大于查表值x.。5= [a+a=1 5.991。这表明此保单组合是非同质的。 01入1+C2A2=1 2.负二项分布。若令负二项分布的均值和方差分别等于 (2) a(A+入1)+a2(A2+A2)=2 观察值x=0.1011和s2=0.1074,则可得参数的矩估计值为 1(A+3A7+A1)+a2(A2+3A径+A2)=a 2 其中α,2,a3为各级样本原点矩。当然,极大似然估 a=-i =1.6049 计值也是容易求得的。 =15.878 B-x 同理,假设保单组合由三种类型的风险构成,其中高风 参数的极大似然估计值为 险的保单(泊松参数为入1)占α,中等风险的保单(泊松参数 &=1.6313,p=16.1384 为A2)占2,低风险的保单(泊松参数为入,)占am,且a1+ 用负二项分布的拟合结果如表6-1-7所示。 %2+a=1,则从保单组合中任意抽取的随机个体保单的索 赔次数分布为 表6-1-7 索赔次数的拟合值:负二项分布 Aie-a Aie-2 索赔次数k 观察值k 拟合值(矩估计)拟合值(极大似然估计) P=a++ k=0.1,2.… 0 96978 96985.5 96980.8 (3) 9240 9222.5 9230.9 三元风险模型的参数估计与二元风险模型类似。 2 704 711.7 708.6 表6-1-5给出了一家保险公司1976年汽车第三者责 43 50.7 50.1 任保险索赔的观察分布。它包括106974辆被保险汽车,每 4 9 3.6 3.4 辆汽车签订一份保单,因此保单数也就是被保险的汽车数。 >4 0 0 0.2 每辆汽车的保险责任都是1976年全年,即没有中途退保的汽 合计 106974 106974.0 106974.0 车,也没有未及时续保的汽车。从表6-1-5的数据容易计 从表6-1-7可以看出,与泊松分布相比,负二项分布的 算出索赔次数的均值为x=0.1011.方差为s2=0.1074。 拟合效果较好。 表6-1-5 索赔次数的观察值 3.泊松一逆高斯分布。泊松一逆高斯分布参数的矩估 计值为 索赔次数 保单数nk f=0.101081,p=0.062979 0 96978 极大似然估计值为7=0.101081,B=0.062698。 1 9240 泊松一逆高斯分布的拟合结果如表6-1-8所示。 2 704 表6-1-8 索赔次数的拟合值:泊松一逆高斯分布 3 43 索赔次数k 观察值d 拟合值(矩估计)拟合值(极大似然估计) 4 9 0 96978 96979.8 96978.5 >4 0 9240 9238.2 9240.4 合计 106974 704 698.4 697.6 下面用各种索赔次数模型对此观察分布进行拟合。 43 53.0 52.9 1.泊松分布。泊松分布参数的矩估计和极大似然估计 9 4.2 4.2 >4 都是观察分布的均值,即无=0.1011。将这一估计值代入泊 0 0 0.4 106974 106974.0 106974.0 松分布的密度函数即得泊松分布的概率P.(k=0,1,2, 合计 ),用此概率乘以样本容量即得索赔次数的拟合值,如表 泊松一逆高斯分布的拟合效果也不错。 6-1-6所示。 4.二元风险模型。二元风险模型参数的矩估计值为
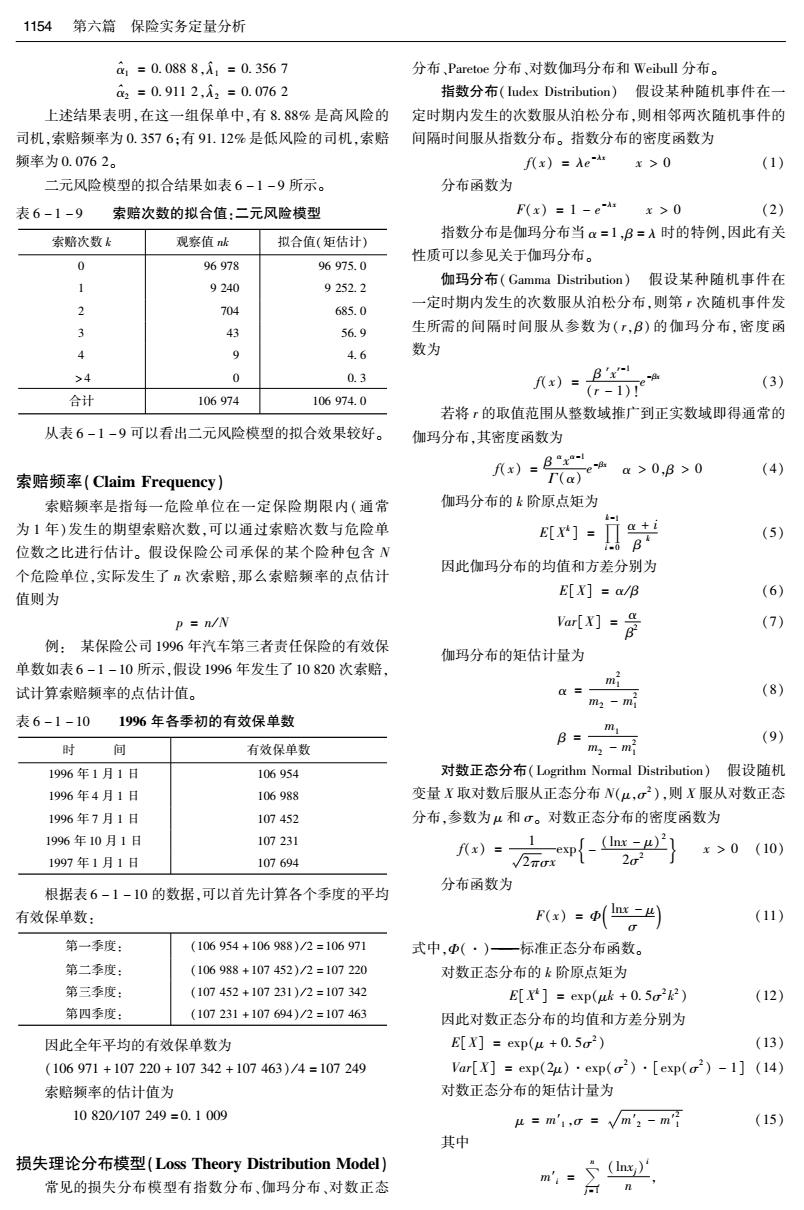
1154第六篇保险实务定量分析 a=0.0888,i,=0.3567 分布,Paretoe分布、对数伽玛分布和Weibull分布。 c2=0.9112,i2=0.0762 指数分布(ludex Distribution)假设某种随机事件在一 上述结果表明,在这一组保单中,有8.88%是高风险的 定时期内发生的次数服从泊松分布,则相邻两次随机事件的 司机,索赔频率为0.3576:有91.12%是低风险的司机,索赔 间隔时间服从指数分布。指数分布的密度函数为 频率为0.0762。 f(x)=Ae x>0 (1) 二元风险模型的拟合结果如表6-1-9所示。 分布函数为 表6-1-9 索赔次数的拟合值:二元风险模型 F(x)=1-e x>0 (2) 指数分布是伽玛分布当x=1,B=A时的特例,因此有关 索赔次数k 观察值k 拟合值(矩估计) 性质可以参见关于伽玛分布。 0 96978 96975.0 伽玛分布(Gamma Distribution)假设某种随机事件在 9240 9252.2 2 704 685.0 一定时期内发生的次数服从泊松分布,则第,次随机事件发 3 43 56.9 生所需的间隔时间服从参数为(T,β)的伽玛分布,密度函 9 4.6 数为 >4 0.3 (3) 合计 106974 106974.0 若将,的取值范围从整数域推广到正实数域即得通常的 从表6-1-9可以看出二元风险模型的拟合效果较好。 伽玛分布,其密度函数为 八x)sEx a>0,B>0 (4) 索赔频率(Claim Frequency) (a)e 索赔频率是指每一危险单位在一定保险期限内(通常 伽玛分布的k阶原点矩为 A- 为1年)发生的期望索赔次数,可以通过索赔次数与危险单 E[X]= +i (5) 位数之比进行估计。假设保险公司承保的某个险种包含N d B 个危险单位,实际发生了次索赔,那么索赔频率的点估计 因此伽玛分布的均值和方差分别为 值则为 E[X]a/B (6) p n/N ar)-合 (7) 例:某保险公司1996年汽车第三者责任保险的有效保 伽玛分布的矩估计量为 单数如表6-1-10所示,假设1996年发生了10820次索赔, 试计算索赔频率的点估计值。 (8) m2-mi 表6-1-10 1996年各季初的有效保单数 B=- m (9) 时 间 有效保单数 m2 -mi 1996年1月1日 106954 对数正态分布(Logrithm Normal Distribution)假设随机 1996年4月1日 106988 变量X取对数后服从正态分布N(μ,2),则X服从对数正态 1996年7月1日 107452 分布,参数为μ和σ。对数正态分布的密度函数为 1996年10月1日 107231 f(x)=- _(lnx-)2 1997年1月1日 107694 一exp{ 2rx 22 x>0(10) 根据表6-1-10的数据,可以首先计算各个季度的平均 分布函数为 有效保单数: )=。) (11) 第一季度: (106954+106988)/2=106971 式中,中(·)一标准正态分布函数。 第二季度: (106988+107452)/2=107220 对数正态分布的k阶原点矩为 第三季度: (107452+107231)/2=107342 E[X exp(uk +0.5) (12) 第四季度: (107231+107694)/2=107463 因此对数正态分布的均值和方差分别为 因此全年平均的有效保单数为 E[X]exp(u +0.52) (13) (106971+107220+107342+107463)/4=107249 Var[X]=exp(2μ)·exp(o2)·[exp(c2)-1](14) 索赔频率的估计值为 对数正态分布的矩估计量为 10820/107249=0.1009 μ=m'1,心=√m'2-m (15) 其中 损失理论分布模型(Loss Theory Distribution Model) 常见的损失分布模型有指数分布、伽玛分布、对数正态 m=(m) n

第1章财产保险业务1155 对数正态分布有一个很好的性质:设a和b是正实数,X k阶原点矩为 是参数为u和2的对数正态分布,则Y=a仍是对数正态 =(-合)B> (31) 分布,参数为u+lna和g2。 Paretoe分布(Paretoe Distribution)Paretoe分布的密度函 由此可见,对数伽玛分布只存在有限阶矩,这是由其密 数为 度函数的厚尾性所决定的。对数伽玛分布的均值和方差分 cB 别为 x)=(B+)丽 x>0 (16) (32) 分布函数为 F(x)=1- B (B+x) (17) a0-(g是广-(6品)》产B>2 (33) k阶原点矩为 α和B的矩估计量为 m'经 a s- m'2-m'月 ELX]-B'k/(a-i) k1 (19) 其中 aB ar[x=(a-1产(a-2 a>2 (20) m,=i1,2 n Paretoe分布的矩估计量为 2(2-m) 损失分布模型的通货膨胀影响(Inflation Effect of = (21)) m2-2m Loss Distribution Model) m m2 B=- (22) 若令X代表历史损失额的随机变量,Y代表模型应用时 m2-2m 期损失额的随机变量,为前后两期之间的通货膨胀率,即Y 其中 =(1+)X,则X与Y的分布函数之间存在如下关系: m,=立 F(y)=P[Y≤y] 分n =P[(x)X≤y] (1) 可以证明,当均值μ=E[X门保持不变,并令a→时,Pa retoe分布收敛到指数分布,分布参数为l/μ。参数为(a,B) =Px≤+] 的Paretoe分布乘以正实数c之后仍然服从Paretoe分布,相 应的分布参数为(α,B)。 J Weibull分布(Weibull Distribution)Weibull分布的概 如果X为连续型随机变量,则X与Y的密度函数之间有 率密度函数为 如下关系: f(x)=crx"-exp(-ex'),c >0,T >0 x >0 (23) (2) 分布函数为 )=, F(x)1-exp(-cx') (24) =(制 Weibull分布的k阶原点矩为 E[X]=cr(/灯+1)k=1,2,… 根据X与Y之间的上述关系式,容易由X的分布函数求 (25) 得Y的分布函数。事实上,除对数伽玛分布以外Y=(1+r)X 因此均值和方差分别为 具有与X相同的分布形式,只是分布参数有如表6-1-11 E[X]=cT(1/F+1) (26) Vam[X]=c2[r(2/x+1)-r2(1/x+1)](27) 所示的变化。 关于τ的矩估计方程为: 表6-1-11 通货膨胀对理论分布模型的影响 lnT(1+2/r)-2lnT(1+1/x)-nm2+lnm1=0 分 布 X的分布参数 Y=(1+r)X的分布参数 (28) 对数正态 μ,r 4+ln(1+r),c Paretoe c的矩估计为 a,B a,(1+r)B 伽玛 e=[I1+] a,B a,B/(1+r) (29) 对数伽玛 a,B 非对数伽玛 m Weibull c.T c/(1+r)1,T 对数伽玛分布(Logrithm Gamma Distribution)对数伽玛 分布的分布函数为F(x)=T(a:lx),密度函数为 fx)=B(Int)a 复合分布(Compound Distribution) x8"r(a) ,a>0,β>0 (30) 索赔次数与赔付额的合成分布在统计学中称作复合分
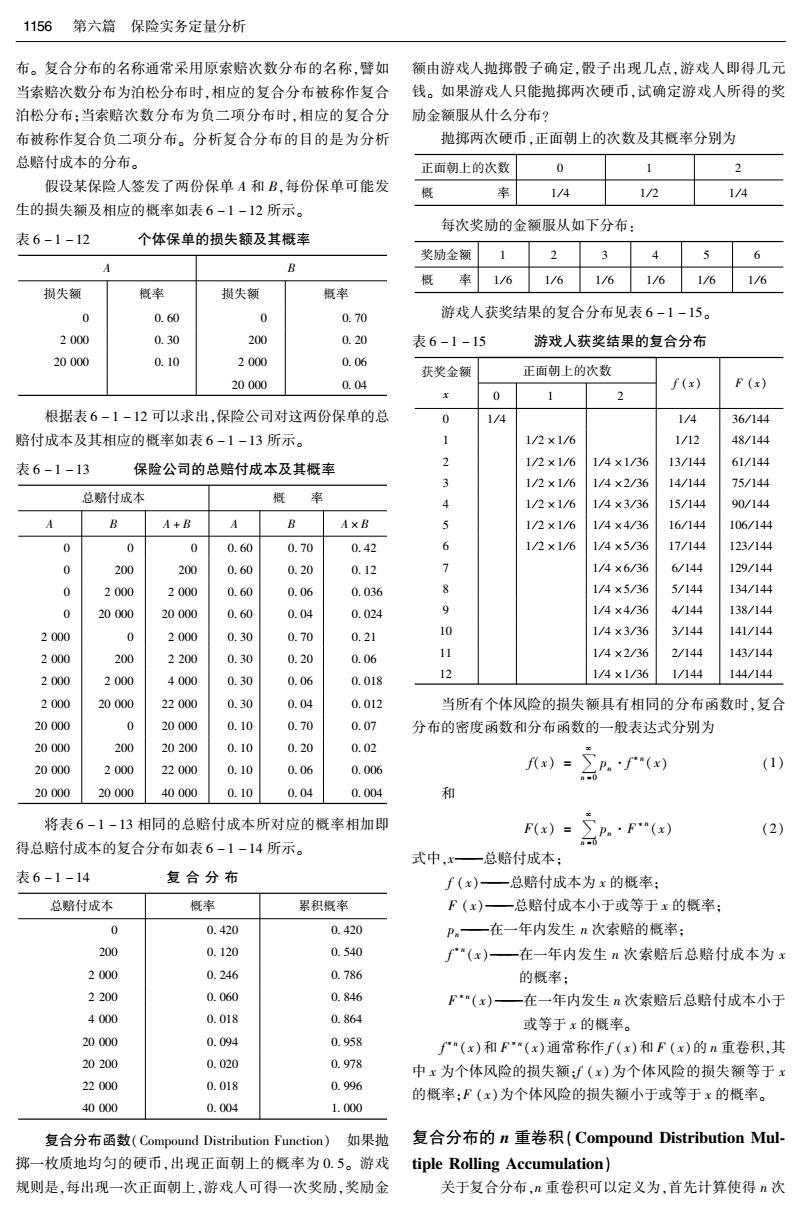
1156第六篇保险实务定量分析 布。复合分布的名称通常采用原索赔次数分布的名称,譬如 额由游戏人抛掷骰子确定,骰子出现几点,游戏人即得几元 当索赔次数分布为泊松分布时,相应的复合分布被称作复合 钱。如果游戏人只能抛掷两次硬币,试确定游戏人所得的奖 泊松分布:当索赔次数分布为负二项分布时,相应的复合分 励金额服从什么分布? 布被称作复合负二项分布。分析复合分布的目的是为分析 抛掷两次硬币,正面朝上的次数及其概率分别为 总赔付成本的分布。 正面朝上的次数 0 假设某保险人签发了两份保单A和B,每份保单可能发 1/4 1/2 1/4 生的损失额及相应的概率如表6-1-12所示。 每次奖励的金额服从如下分布: 表6-1-12 个体保单的损失额及其概率 奖励金额 1 2 3 4 5 6 6 概 率 1/6 1/6 1/6 1/6 1/6 1/6 损失额 概率 损失额 概率 0 0.60 0 0.70 游戏人获奖结果的复合分布见表6-1-15。 2000 0.30 200 0.20 表6-1-15 游戏人获奖结果的复合分布 20000 0.10 2000 0.06 获奖金额 正面朝上的次数 20000 0.04 f(x) F(x) 0 1 2 根据表6-1-12可以求出,保险公司对这两份保单的总 0 4 1/4 36/144 赔付成本及其相应的概率如表6-1-13所示。 1/2×1/6 1/12 48/144 表6-1-13 保险公司的总赔付成本及其概率 2 1/2×1/6 1/4×1/36 13/144 61/144 3 1/2×1/6 1/4×2/36 14/144 75/144 总黯付成本 概 率 4 1/2×1/6 1/4×3/36 15/144 90/144 B A+B AxB 1/2×1/6 1/4×4/36 16/144 106/144 0 0 0 0.60 0.70 0.42 6 1/2×1/6 1/4×5/36 17/144 123/144 0 200 200 0.60 0.20 0.12 7 1/4×6/36 6/144 129/144 0 2000 2000 0.60 0.06 0.036 8 1/4×5/36 5/144 134/144 0 20000 20000 0.60 0.04 0.024 1/4×4/36 4/144 138/144 2000 2000 0.30 0.70 0.21 o 1/4×3/36 3/144 141/144 2000 200 2200 0.30 0.20 0.06 11 1/4×2/36 2/144 143/144 12 1/144 2000 2000 4000 0.30 0.06 0.018 1/4×1/36 144/144 2000 20000 22000 0.30 0.04 0.012 当所有个体风险的损失额具有相同的分布函数时,复合 20000 20000 0.10 0.70 0.07 分布的密度函数和分布函数的一般表达式分别为 20000 200 20200 0.10 0.20 0.02 20000 2000 22000 0.10 0.06 0.006 fx)=∑p.f(x) n0 20000 20000 40000 0.10 0.04 0.004 和 将表6-1-13相同的总赔付成本所对应的概率相加即 F)=A.·F() (2) 得总赔付成本的复合分布如表6-1-14所示。 n=0 式中,x一总赔付成本: 表6-1-14 复合分布 f(x)一总赔付成本为x的概率: 总赔付成本 概率 累积概率 F(x)一总赔付成本小于或等于x的概率: 0 0.420 0.420 P。一在一年内发生n次索赔的概率: 200 0.120 0.540 “(x)一在一年内发生n次索赔后总赔付成本为x 2000 0.246 0.786 的概率: 2200 0.060 0.846 F“(x)一在一年内发生n次索赔后总赔付成本小于 4000 0.018 0.864 或等于x的概率。 20000 0.094 0.958 f"(x)和F(x)通常称作f(x)和F(x)的n重卷积,其 20200 0.020 0.978 中x为个体风险的损失额∫(x)为个体风险的损失额等于x 22000 0.018 0.996 的概率:F(x)为个体风险的损失额小于或等于x的概率。 40000 0.004 1.000 复合分布函数(Compound Distribution Function) 如果抛 复合分布的n重卷积(Compound Distribution Mul- 掷一枚质地均匀的硬币,出现正面朝上的概率为0.5。游戏 tiple Rolling Accumulation) 规则是,每出现一次正面朝上,游戏人可得一次奖励,奖励金 关于复合分布,n重卷积可以定义为,首先计算使得n次

第1章财产保险业务1157 索赔的总赔付成本为x的各种可能组合,然后将各种可能组 F“(x)=F*Fa-)(x) (2) 合出现的概率相加。 我们这里以游戏人抛掷三次骰子为例,试计算他的获奖 上述定义既适用于个体风险的损失额为同分布的情形, 金额服从什么分布。 也适用于非同分布的情形,对于两个不同的分布∫(x)和 若记一次抛掷结果的获奖金额服从概率函数为∫(x)的 g(x),它们的卷积可记为f(x)'g(x)。因此n重卷积也可 分布,则三次抛掷的获奖金额服从∫(x)的三重卷积。∫(x) 以分解为 的二重卷积在表6-1-15第4栏已得到,因此f(x)的三重 产“(x)=f*fa-)(x) (1) 卷积可以通过计算f(x)的二重卷积与∫(x)的卷积得到。具 和 体结果如表6-1-16所示。 表6-1-16 f(x)的三重卷积 f(x) 广2(x) f(x)"f2(x) f3(x) 1 1/6 1/6 1/36 3 1/6 2/36 1/6×1/36 1/216 4 1/6 3/36 1/6×2/36+1/6×1/36 3/216 5 1/6 4/36 1/6×3/36+1/6×2/36+1/6×1/36 6/216 6 1/6 5/36 1,/6×4/36+1/6×3/36+1/6×2/36+1/6×1/36 10/216 > 6/36 1/6×5/36+1/6×4/36+1/6×3/36+1/6×2/36+1/6×1/36 15/216 8 5/36 1/6×6/36+1/6×5/36+1/6×4/36+1/6×3/36+1/6×2/36+1/6×1/36 21/216 9 4/36 1/6x×5/36+1/6×6/36+1/6×5/36+1/6×4/36+1/6×3/36+1/6×2/36 25/216 0 3/36 1/6×4/36+1/6×5/36+1/6×6/36+1/6×5/36+1/6×4/36+1/6×3/36 27/216 11 2/36 1/6×3/36+1/6×4/36+1/6×5/36+1/6×6/36+1/6×5/36+1/6×4/36 27/216 12 1/36 1/6×2/36+1/6×3/36+1/6×4/36+1/6×5/36+1/6×6/36+1/6×536 25/216 13 1/6×2/36+1/6×2/36+1/6×3/36+1/6×4/36+1/6×5/36+1/6×6/36 21/216 14 1/6×2/36+1/6×2/36+1/6×3/36+1/6×4/36+1/6×5/36 15/216 的 1/6×2/36+1/6×2/36+1/6×3/36+1/6×4/36 10/216 16 1/6×2/36+1/6×2/36+1/6×3/36 6/216 公 1/6×2/36+1/6×2/36 3/216 18 1/6×1/36 1/216 下面我们给出卷积的数学定义。对于两个离散型的概 xe 率函数f(x)和g(x),它们的卷积厂g(x)被定义为 因此 fg(x)=∑fy)g(x-y) (3) F2(x)=2(y)d山 同样,两个连续型密度函数的卷积可定义为 =[yedy (7) fg(x)=fy)g(x-y)山 (4) =1-(1+x)e 应用Stieltjes积分,上两个卷积公式可表述为 计算复合分布的均值需要应用条件概率的一些结果。 若令N表示索赔次数的随机变量;X(i=1,2,…,N)表示 fg(x)=g(x-y)dF(y) (5) 每次赔付额的随机变量,且X,(i=1,2,…,N)独立同分布, 指数分布的二重卷积(Duplicate Rolling Accumulation of 则关于总赔付成本的随机变量可以表述为 Index Distribution)指数分布的密度函数为f(x)=e, S=X1+X2+…+X。 (8) x>0。由卷积的计算公式(4)式得 若记E[N]=n,E[X[X,]]=m,则有 E[S]=EE[SI N] fr2(x)=f)x-y)d西y =EINE[X, (9) E[mN] feve-(dy (6) nm 复合泊松分布的均值等于其方差,即E[N]=Var[N]= n,同时若令Var[X,]=c2,则有 Var[S]Var E[SI N]+E Var[SI N]