
第八章 非标准化期权的解析法定价 马文婧李娜阮佳佳程钰
第八章 非标准化期权的解析法定价 马文婧 李娜 阮佳佳 程钰
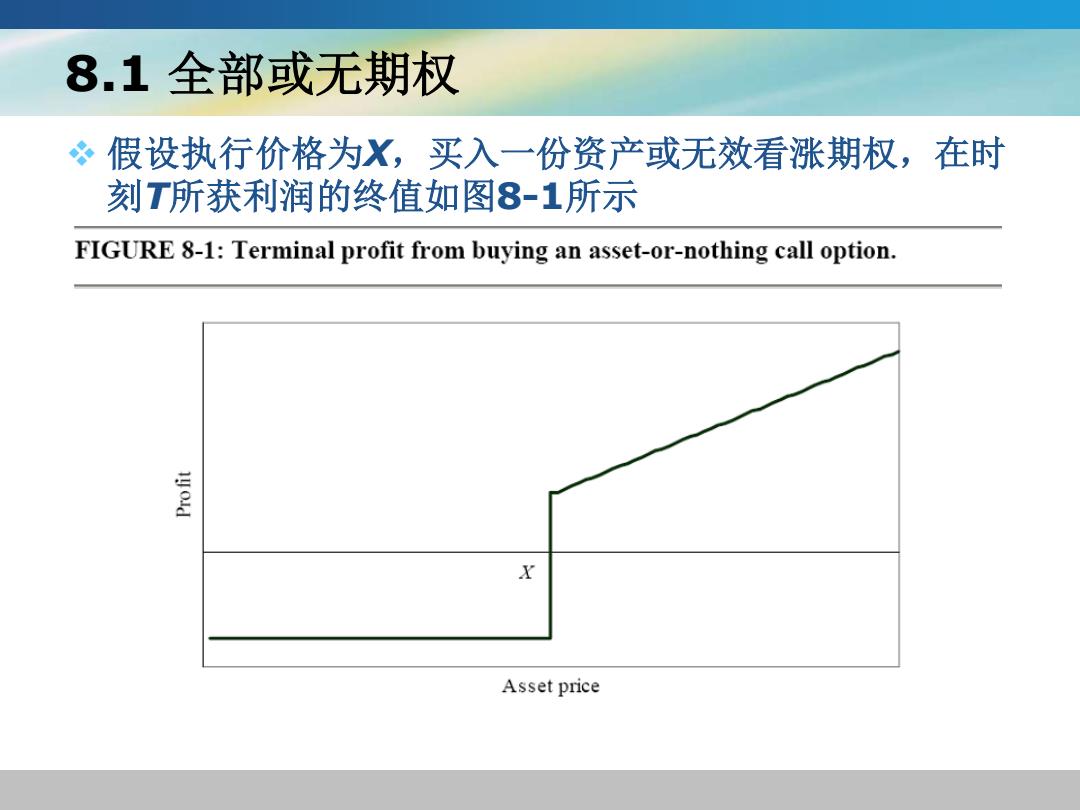
8.1全部或无期权 ?假设执行价格为X,买入一份资产或无效看涨期权,在时 刻T所获利润的终值如图8-1所示 FIGURE 8-1:Terminal profit from buying an asset-or-nothing call option. X Asset price
8.1 全部或无期权 ❖ 假设执行价格为X,买入一份资产或无效看涨期权,在时 刻T所获利润的终值如图8-1所示

在BSM假设下,资产或无效欧式期权的价值为 Cov(X,T)=e"N(d) 其中 dIn(Sedd aT
❖在BSM假设下,资产或无效欧式期权的价值为 其中

购买1美元现金或无效看涨期权的期末利润如图8-2所示 FIGURE 8-2:Terminal profit from buying a cash-or-nothing call option. 复 X Asset price 冬在BSM假设下,现金或无效欧式期权的价值为 Ccov(X:T)=e"N(d2)
❖ 购买1美元现金或无效看涨期权的期末利润如图8-2所示 ❖ 在BSM假设下,现金或无效欧式期权的价值为

标准化欧式看涨期权赋予持有人在时刻T按照约 定价格X购买当前价格为S的基础资产的权利。 冬要构建这样一个标准化看涨期权,我们可以买入 S单位的资产或无效看涨期权,卖出X单位的现金 或无效看涨期权。因此,按照复制定价原则,标 准化欧式看涨期权的价值为 Casu Se "N(d)-Xe "N(d)
❖标准化欧式看涨期权赋予持有人在时刻T按照约 定价格X购买当前价格为S的基础资产的权利。 ❖要构建这样一个标准化看涨期权,我们可以买入 S单位的资产或无效看涨期权,卖出X单位的现金 或无效看涨期权。因此,按照复制定价原则,标 准化欧式看涨期权的价值为

。1单位资产或无效看跌期权价值为 Paov(X.T)=e "N(-d) 。1美元现金或无效看跌期权价值为 Pcov(X.T)=e"N(-d)
❖1单位资产或无效看跌期权价值为 ❖1美元现金或无效看跌期权价值为

冬标准化欧式看跌期权赋予持有人在时刻T按照约 定的价格X卖出当前价格为S的基础资产的权利。 冬要构建这样的标准化看跌期权,我们卖出S单位 的资产或无效看跌期权,买入X单位的现金或无 效看跌期权。因此,标准化欧式看跌期权的价值 为 Pasu Xe N(-d2)-Se "N(-d)
❖标准化欧式看跌期权赋予持有人在时刻T按照约 定的价格X卖出当前价格为S的基础资产的权利。 ❖要构建这样的标准化看跌期权,我们卖出S单位 的资产或无效看跌期权,买入X单位的现金或无 效看跌期权。因此,标准化欧式看跌期权的价值 为

例8-1: 假设你的叔叔告诉你,如果六个月后XYZ公司的股票价 格大于100美元,他将给你100美元。XYZ公司股票当 前的价格为90美元每股,股息收益率为1%,波动率为 206,无风险利率为3%。你叔叔送你这个礼物的价值 是多少? Seir=90e0.0io5)=89.551,Xer=100e0.o305)=98.551. 4,=h(89.51/98.510-0.50.20)0.5-0.7450. 0.200.5 ccow=e0305)W(-0.7450)×100 =24.453
❖ 例8-1: 假设你的叔叔告诉你,如果六个月后XYZ公司的股票价 格大于100美元,他将给你100美元。XYZ公司股票当 前的价格为90美元每股,股息收益率为1%,波动率为 20%,无风险利率为3%。你叔叔送你这个礼物的价值 是多少?

8.1.1全部或无期权的风险度量 FIGURE 8-3:Numerical approximation for the delta of a put option. anJeA uondO -OV(S+)-Ov(S) (S+)-(S-) OV(S+)-OV(S-0) OV(S-6) 20 OV(S+9) S-6 S S+中 Asset price
8.1.1 全部或无期权的风险度量

Y反映的是资产价格变化所引起的△变化,可利用 以下公式来计算: OV(S+)-2xOV(S+)+OV(S-) Y= 2
❖ γ反映的是资产价格变化所引起的∆变化,可利用 以下公式来计算: