
第7章标准化期权 的解析法定价 朱子川接小波张翠萍 杨杨
第7章 标准化期权 的解析法定价 朱子川 接小波 张翠萍 杨杨

背景 第6章中,推导了期权价格关系式。仅指明了价格的边界, 而非精确的期权价值。本章推导欧式期权的定价公式,将该 公式用于风险管理,如何估计定价公式中的参数。 女 期权的定价也是未来现金流的现值。看涨期权的预期现金流 取决于:基础资产经风险调整的预期价格升值率。贴现率是期 权经风险调整的预期回报率。该传统定价法的一个问题是, 要准确估计风险调整的预期回报参数是非常困难的 1973年,随着Black和Scholes(1973)以及Merton(1973) (BSM)在期权和其基础资产之间构建一个无风险套期保值, 期权定价就与个人风险偏好无关,假设个体是风险中性的。 所有资产的预期回报率等于它们的无风险利率
背景 ❖ 第6章中,推导了期权价格关系式。仅指明了价格的边界, 而非精确的期权价值。本章推导欧式期权的定价公式,将该 公式用于风险管理,如何估计定价公式中的参数。 ❖ 期权的定价也是未来现金流的现值。看涨期权的预期现金流 取决于:基础资产经风险调整的预期价格升值率。贴现率是期 权经风险调整的预期回报率。该传统定价法的一个问题是, 要准确估计风险调整的预期回报参数是非常困难的。 ❖ 1973年,随着Black和Scholes (1973)以及Merton (1973) (BSM)在期权和其基础资产之间构建一个无风险套期保值, 期权定价就与个人风险偏好无关,假设个体是风险中性的。 所有资产的预期回报率等于它们的无风险利率

内容 第一节风险中性定价的直觉分析 。第二节给定正态分布回报率的均值和方差, 推导了资产预期价值的表达式。 ·第三节欧式看涨期权的定价公式。 ·第四节欧式看跌期权的定价公式。 ~第五节说明如何利用期权定价公式去度量期 权的风险特征。 心最后一节是结论
内容 ❖ 第一节风险中性定价的直觉分析 ❖ 第二节给定正态分布回报率的均值和方差, 推导了资产预期价值的表达式。 ❖ 第三节欧式看涨期权的定价公式。 ❖ 第四节欧式看跌期权的定价公式。 ❖ 第五节说明如何利用期权定价公式去度量期 权的风险特征。 ❖ 最后一节是结论

7.1风险中性定价的直觉分析 ÷7.1.1利用二项式模型构建无风险保值组合 ·欧式看涨期权,三个月后X=40。假设S=40, 三个月后资产的价格是45或35。这些资产价格 列于下图7-1.3个月后为45,则看涨期权价值 为5;如果资产价格3个月后为35,期权价值为 0
7.1 风险中性定价的直觉分析 ❖ 7.1.1 利用二项式模型构建无风险保值组合 ❖ 欧式看涨期权,三个月后X=40。假设S=40, 三个月后资产的价格是45或35。这些资产价格 列于下图7-1。3个月后为45,则看涨期权价值 为5;如果资产价格3个月后为35,期权价值为 0
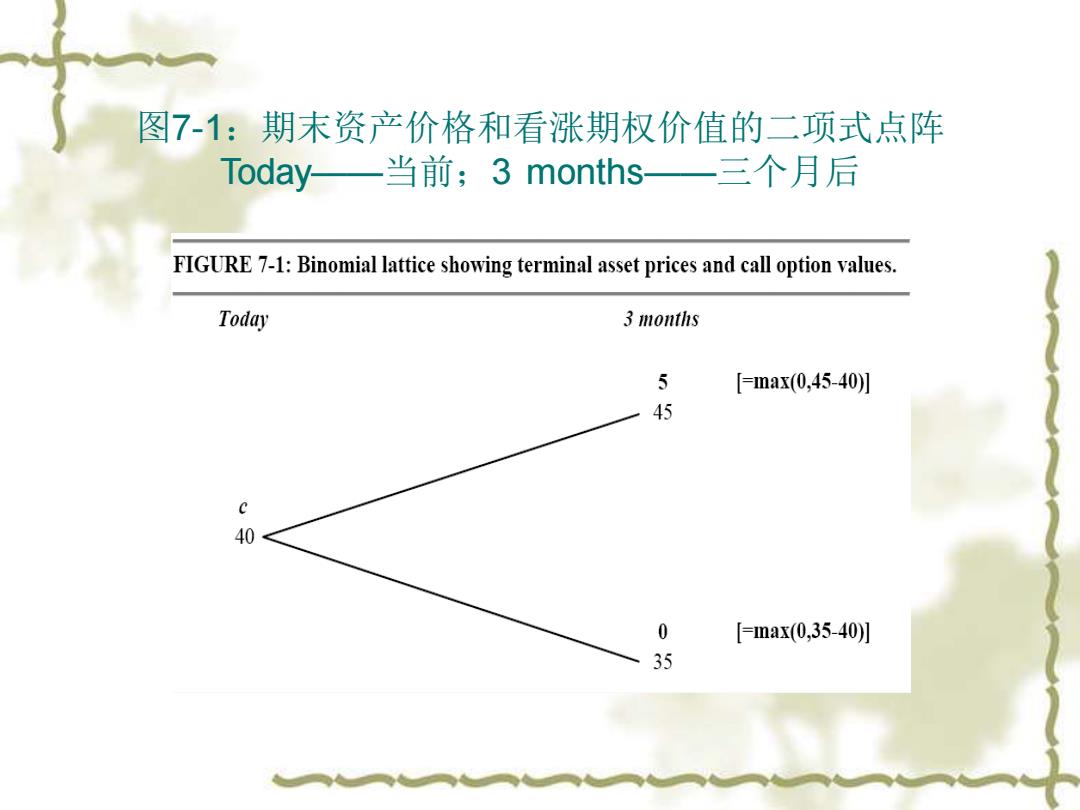
图7-1:期末资产价格和看涨期权价值的二项式点阵 Today-一当前;3 months-一三个月后 FIGURE 7-1:Binomial lattice showing terminal asset prices and call option values. Today 3 months 5 [=max(0,45-40)1 45 40 0 [=max(0,35-40)1 35
图7-1:期末资产价格和看涨期权价值的二项式点阵 Today——当前;3 months——三个月后

一买入一单位资产并卖出门份看涨期权 ÷我们令n满足45-5n=35,卖出两份看涨期权(即n=2) 可以消除所有组合风险。R=2%,欧式看涨期权的价格 为2.84。 多 在无风险套利情况下,现在构建无风险组合的成本满足:40- 2c=35/1.02 ,无成本套利机会 假设看涨期权价格为3,卖出看涨期权,买入0.5单位资 产,并借款17.16(即35的一半的现值),产生现金 3-0.5(40)+17.16=0.16到期时,到期S=45,组合价值为 -(45-40)+0.5(45)-17.50=0 ÷如果S=35,组合价值为0+0.5(35)-17.50=0
买入一单位资产并卖出n份看涨期权 ❖ 我们令n满足45−5n=35,卖出两份看涨期权(即n=2) 可以消除所有组合风险。R= 2%,欧式看涨期权的价格 为2.84。 ❖ 在无风险套利情况下,现在构建无风险组合的成本满足:40- 2c=35/1.02 ❖ 无成本套利机会 ❖ 假设看涨期权价格为3,卖出看涨期权,买入0.5单位资 产,并借款17.16(即35的一半的现值),产生现金 3-0.5(40)+17.16=0.16到期时,到期S=45,组合价值为 −(45−40)+0.5(45)−17.50=0 ❖ 如果S=35,组合价值为0+0.5(35)−17.50=0

TABLE 7-1:Arbitrage portfolio trades. Value in 3 months Trades Initial investment Sx=35 Sr=45 Sell call 3 0 -(45-40) Buy asset -20 .535)=17.50 .5(45)=22.50 Sell risk-free bonds 17.16 -17.50 -17.50 Net portfolio value .16 0 0

7.1.2风险中性假设下二项式模型定价 在风险中性下,其中p是上界的概率,1-p是下界 的概率 40(1.02)=45p+35(1-p), 然后求解上段风险中性的概率p,等于58%。 交 找出概率后,就可计算看涨期权的预期终值 为 看涨期权的预期价值=5(.58)+0(.42)=2.90。 必 看涨期权的现值是预期终值的贴现。 2.90 C= =2.84 1.02 该值与利用无风险保值组合法计算的结果完全 一样
7.1.2风险中性假设下二项式模型定价 ❖ 在风险中性下,其中p是上界的概率,1−p是下界 的概率, 40(1.02) =45p +35(1−p), ❖ 然后求解上段风险中性的概率p,等于58%。 ❖ 找出概率后,就可计算看涨期权的预期终值 为 看涨期权的预期价值=5(.58) +0(.42) =2.90。 ❖ 看涨期权的现值是预期终值的贴现。 2.90 2.84 1.02 c = = 该值与利用无风险保值组合法计算的结果完全 一样

7.1.3风险厌恶假设下二项式模型定价 找到基础资产经风险调整的预期回报率,以便计算资产的预期终 值 的 找到看涨期权的经风险调整的预期回报率,以便将看涨期权的终 值贴现为现值。 假设未来三个月资产的预期升值率为4%—2%的无风险回报落 加2%的个人风险溢价率。因为当前资产价格为40,预期回报率 为4%,所以风险厌恶假设下上界概率p'和下界概率1-p'必须满 足 必 40(1.04)=45p'+35(1-p) 风险厌恶假设下,上界概率为66%。风险厌恶个体的上界概率高 于风险中性个体的上界概率(假设二项式模型中资产价格终值相 同),这是因为,给定资产价格终值保持不变,风险厌恶下更高 的预期回报率必须对应更高的上界概率。 E(cr)=5(0.66)+0(0.34)=3.30
7.1.3 风险厌恶假设下二项式模型定价 ❖ 找到基础资产经风险调整的预期回报率,以便计算资产的预期终 值 ❖ 找到看涨期权的经风险调整的预期回报率,以便将看涨期权的终 值贴现为现值。 ❖ 假设未来三个月资产的预期升值率为4%——2%的无风险回报率 加2%的个人风险溢价率。因为当前资产价格为40,预期回报率 为4%,所以风险厌恶假设下上界概率 p‘和下界概率 1- p’必须满 足 ❖ 40(1.04)=45 p' +35(1- p') 风险厌恶假设下,上界概率为66%。风险厌恶个体的上界概率高 于风险中性个体的上界概率(假设二项式模型中资产价格终值相 同),这是因为,给定资产价格终值保持不变,风险厌恶下更高 的预期回报率必须对应更高的上界概率。 ( ) 5(0.66) 0(0.34) 3.30 ~ E cT = + =

。前面第3章我们已推导了预期收益和风险之间的取舍关 系,该关系称为资本资产定价模型(CAPM),也表明 资产的预期回报率为 E、=r+(EM-r)P (7-1) 其中,Es是资产的预期回报率,E是市场组合的预期回报率,r是无风险回报率,Bs是 资产的贝塔风险。 在(7-1)式预期收益/风险取舍关系式中,资产的贝塔B、是相对于市场水平1%的变化, 资产价格变化的百分比。因为CAPM模型适用于所有风险资产,包括看涨期权,因此看涨 期权的预期收益率可表示为 Ec=r+(Ew-r)βc (7-2) 其中,看涨期权的贝塔β℃是相对于市场水平1%的变化,看涨期权价格变化的百 分比。用βs乘以看涨期权价格相对于资产价格的变化百分比,即可得看涨期权的 贝塔 dclc B。=Bs dsIS
❖ 前面第3章我们已推导了预期收益和风险之间的取舍关 系,该关系称为资本资产定价模型(CAPM),也表明 资产的预期回报率为 S M S E = r + (E − r) (7-1) 其中,Es是资产的预期回报率,EM是市场组合的预期回报率,r是无风险回报率,S是 资产的贝塔风险。 在(7-1)式预期收益/风险取舍关系式中,资产的贝塔S是相对于市场水平1%的变化, 资产价格变化的百分比。因为CAPM模型适用于所有风险资产,包括看涨期权,因此看涨 期权的预期收益率可表示为 EC= r +(EM - r) C (7-2) 其中,看涨期权的贝塔c是相对于市场水平1%的变化,看涨期权价格变化的百 分比。用S乘以看涨期权价格相对于资产价格的变化百分比,即可得看涨期权的 贝塔 = dS S dc c c S / /