
第六章无套利价格关系式: 期权
1 第六章 无套利价格关系式: 期权

本章主要内容: ·6.1期权和远期合约 ·6.2连续变动率 ·6.3离散现金流 。6.4期货期权的无套利关系 ·6.5市场间的无套利关系
2 • 6.1期权和远期合约 • 6.2连续变动率 • 6.3离散现金流 • 6.4期货期权的无套利关系 • 6.5市场间的无套利关系 本章主要内容:

关于无套利定价法: 在不需要期初投资的条件下,交易者在金融资产交易中转 移资金,从而赚取无风险利润: 套利的两种常用方法: 1现在进行净支出为零,在将来产生正的收益; 2.现在产生正的收益,在将来不会产生净支付:
3 关于无套利定价法: • 在不需要期初投资的条件下,交易者在金融资产交易中转 移资金,从而赚取无风险利润; • 套利的两种常用方法: 1.现在进行净支出为零,在将来产生正的收益; 2.现在产生正的收益,在将来不会产生净支付;

6.1期权和远期合约 两个区别: 远期净持有成本为零,期权需要投资费用: 权利与义务的区别: S,-X,如果S,≥X 多头看涨期权收益: 0 如果Sx<X 多头看涨期权利润: S,-X-ce”,如果S,≥X -ce", 如果S,<X 兀空头看涨,T二一兀多头看涨,T
4 6.1期权和远期合约 两个区别: • 远期净持有成本为零,期权需要投资费用; • 权利与义务的区别; 多头看涨期权收益: 多头看涨期权利润:

6.1期权和远期合约(续) 看涨期权多头与空头的期末利润: FIGURES 6-2a and 6-2b:Terminal profit of long and short call positions. (a) (b) Profit,πr Profit,πr Cerr -cerr S St Sr-X-ceT Sr-X-ceT
5 6.1期权和远期合约(续) 看涨期权多头与空头的期末利润:
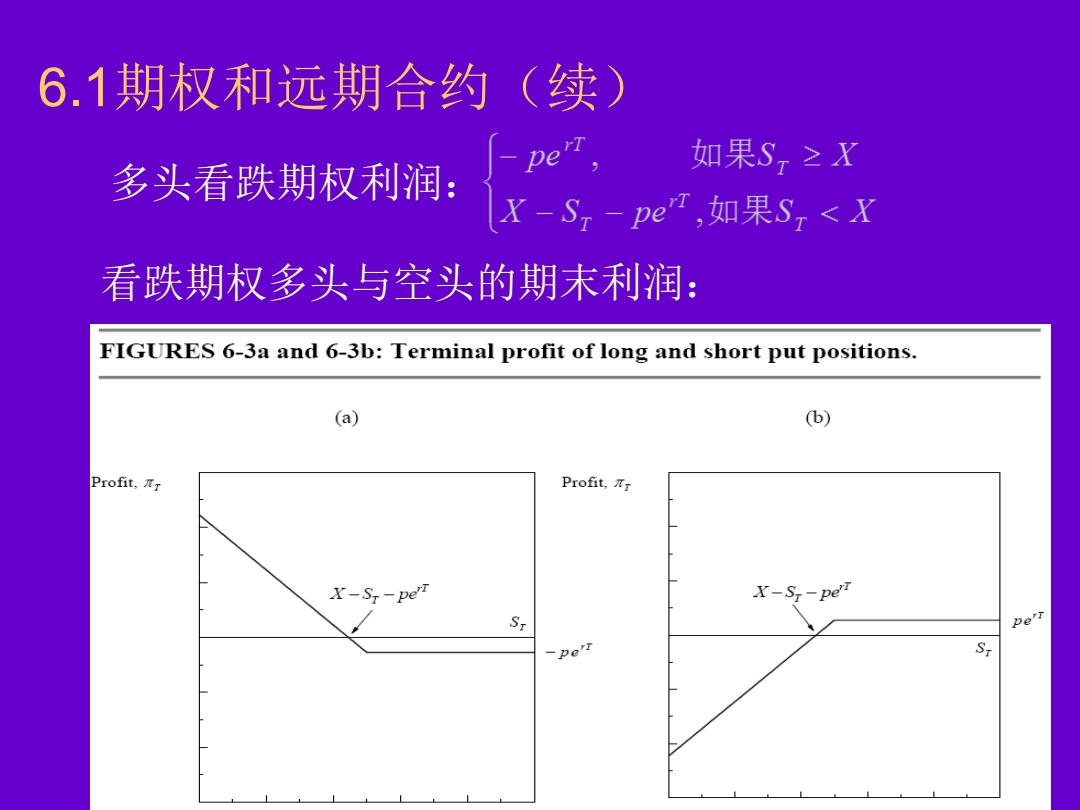
6.1期权和远期合约(续) 多头看跌期权利润: pe", - 如果S,≥X X-S,-pe,如果S,<X 看跌期权多头与空头的期末利润: FIGURES 6-3a and 6-3b:Terminal profit of long and short put positions. (a) (b) Profit,πr Profit,πr X-St-pefT X-St-peT ST De'r -pe'r S
6 6.1期权和远期合约(续) 多头看跌期权利润: 看跌期权多头与空头的期末利润:
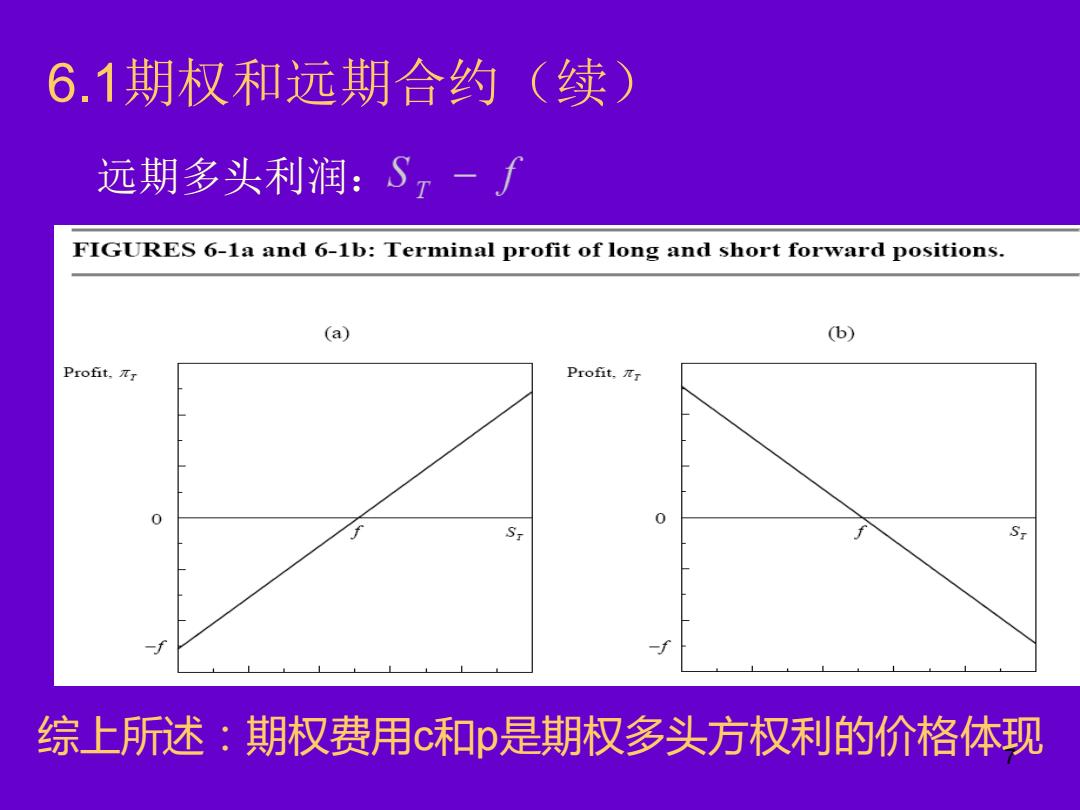
6.1期权和远期合约(续) 远期多头利润:S, FIGURES 6-1a and 6-1b:Terminal profit of long and short forward positions. (a) (b) Profit,πr Profit.πr 0 S S 综上述:期权费用c和是期权多头方权利的价格体现
7 6.1期权和远期合约(续) 远期多头利润: 综上所述:期权费用c和p是期权多头方权利的价格体现

6.1期权和远期合约(续) 看涨期权和看跌期权利润与远期合约利润的关系: 远期可由看涨期权多头和看跌期权空头构建: S=X-ce+pe,如果S7≥X . p.T S,-X-ce+pe,如果S,<X =ST-X-ce"!pe" 如果: f X+ce"-pem πc,r-元p.x=S7-f1 看涨期权多头与看跌期权空头的净头寸与远期相似 事实上,远期合约可由看张期权和看跌期权来构建
8 6.1期权和远期合约(续) 看涨期权和看跌期权利润与远期合约利润的关系: 远期可由看涨期权多头和看跌期权空头构建; 如果: 看涨期权多头与看跌期权空头的净头寸与远期相似, 事实上,远期合约可由看涨期权和看跌期权来构建

6.1期权和远期合约(续) 所有的衍生合约都可由以下这些基本工具中的任何 一个来构建: (1)远期合约和看涨期权: (2)远期合约和看跌期权; (③)看涨期权和看跌期权; 问题:既然所有的衍生合约可由远期和期权来构建,而 远期可由看涨期权和看跌期权来构建,那么任何衍生合 约都可由期权来构建?
10 6.1期权和远期合约(续) 所有的衍生合约都可由以下这些基本工具中的任何 一个来构建: (1)远期合约和看涨期权; (2)远期合约和看跌期权; (3)看涨期权和看跌期权; 问题:既然所有的衍生合约可由远期和期权来构建,而 远期可由看涨期权和看跌期权来构建,那么任何衍生合 约都可由期权来构建?

6.2连续变动率 利息成本收益为连续,这与在离散现金流假设下相同;非 利息成本收益亦为连续,这与离散现金流的假设不同; 利息持有成本收益为(为无风险利率),非利息持有成本/ 收益为(可正可负); 6.2.1欧式看涨期权的价格下限 c≥最大值(0,Ser=XeI) c≥0 c≥Seir-Xem
11 • 利息成本/收益为连续,这与在离散现金流假设下相同;非 利息成本/收益亦为连续,这与离散现金流的假设不同; • 利息持有成本/收益为r(为无风险利率),非利息持有成本/ 收益为i(可正可负); 6.2连续变动率 6.2.1 欧式看涨期权的价格下限