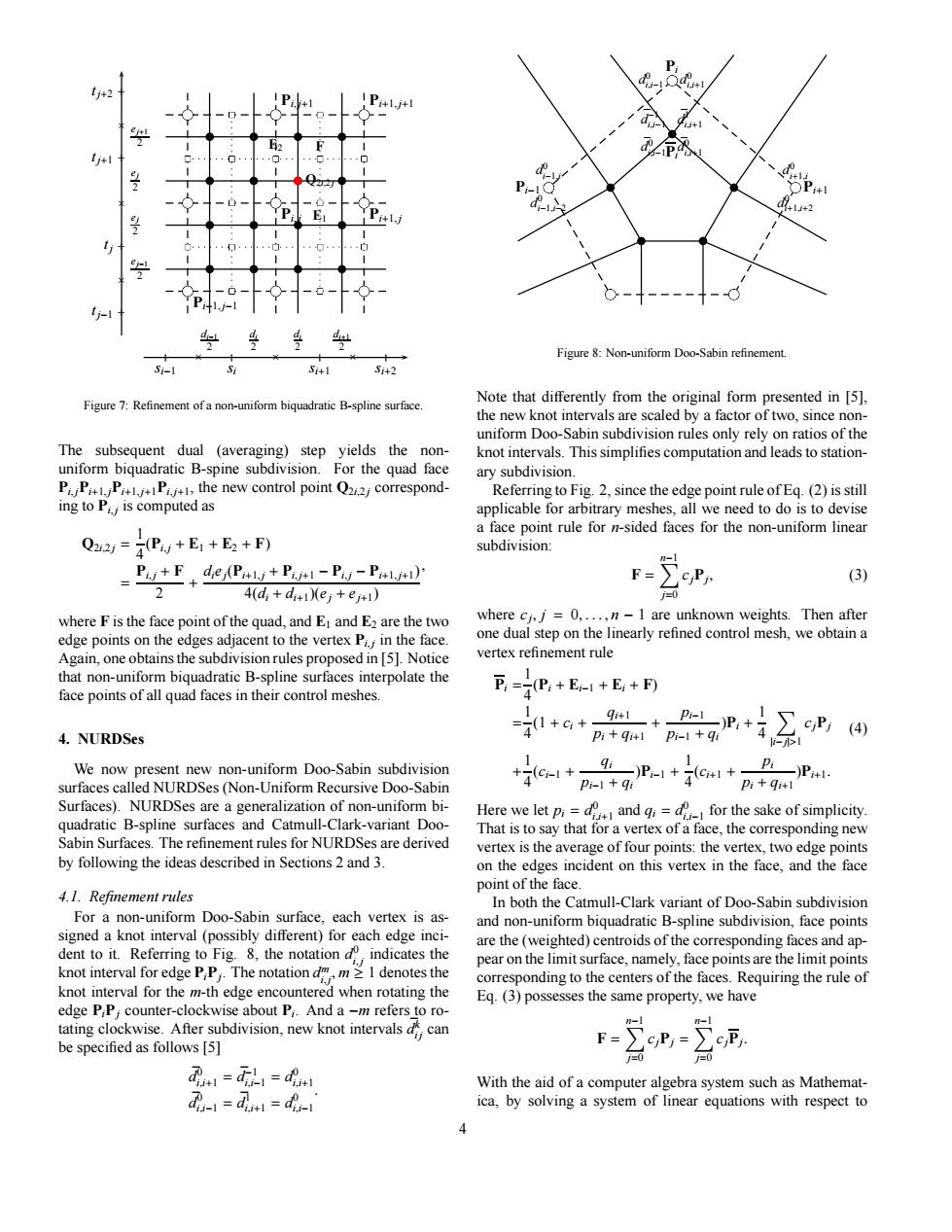
O-,+E,+E2+F F-Zep 下=P,+E+E+ +a+n+e +c+P+o1+fnP E.(3)p0s F-Xcr,-ZoF, bc bc bc bc bc bc bc bc bc rs rs rs rs rs rs rs rs rs rs rs rs rs rs rs rs b b b b b b b b b b b b b b b b b E1 E2 F Pi, j Pi+1, j Pi, j+1 Pi+1, j+1 Pi−1, j−1 Q2i,2 j | | | | × × × si−1 si si+1 si+2 di−1 2 di 2 di 2 di+1 2 + + + + × × × tj−1 tj tj+1 tj+2 ej−1 2 ej 2 ej 2 ej+1 2 Figure 7: Refinement of a non-uniform biquadratic B-spline surface. The subsequent dual (averaging) step yields the non￾uniform biquadratic B-spine subdivision. For the quad face Pi, jPi+1, jPi+1, j+1Pi, j+1, the new control point Q2i,2 j correspond￾ing to Pi, j is computed as Q2i,2 j = 1 4 (Pi, j + E1 + E2 + F) = Pi, j + F 2 + diej(Pi+1, j + Pi, j+1 − Pi, j − Pi+1, j+1) 4(di + di+1)(ej + ej+1) , where F is the face point of the quad, and E1 and E2 are the two edge points on the edges adjacent to the vertex Pi, j in the face. Again, one obtains the subdivision rules proposed in [5]. Notice that non-uniform biquadratic B-spline surfaces interpolate the face points of all quad faces in their control meshes. 4. NURDSes We now present new non-uniform Doo-Sabin subdivision surfaces called NURDSes (Non-Uniform Recursive Doo-Sabin Surfaces). NURDSes are a generalization of non-uniform bi￾quadratic B-spline surfaces and Catmull-Clark-variant Doo￾Sabin Surfaces. The refinement rules for NURDSes are derived by following the ideas described in Sections 2 and 3. 4.1. Refinement rules For a non-uniform Doo-Sabin surface, each vertex is as￾signed a knot interval (possibly different) for each edge inci￾dent to it. Referring to Fig. 8, the notation d 0 i, j indicates the knot interval for edge PiPj . The notation d m i, j , m ≥ 1 denotes the knot interval for the m-th edge encountered when rotating the edge PiPj counter-clockwise about Pi . And a −m refers to ro￾tating clockwise. After subdivision, new knot intervals d¯k i j can be specified as follows [5] d¯0 i,i+1 = d¯−1 i,i−1 = d 0 i,i+1 d¯0 i,i−1 = d¯1 i,i+1 = d 0 i,i−1 . bc bc bc bc bc b b b b b Pi d 0 i,i+1 d 0 i,i−1 Pi−1 d 0 i−1,i d 0 i−1,i−2 Pi+1 d 0 i+1,i d 0 i+1,i+2 Pi d¯0 i,i+1 d¯0 i,i−1 d¯1 i,i+1 d¯−1 i,i−1 Figure 8: Non-uniform Doo-Sabin refinement. Note that differently from the original form presented in [5], the new knot intervals are scaled by a factor of two, since non￾uniform Doo-Sabin subdivision rules only rely on ratios of the knot intervals. This simplifies computation and leads to station￾ary subdivision. Referring to Fig. 2, since the edge point rule of Eq. (2) is still applicable for arbitrary meshes, all we need to do is to devise a face point rule for n-sided faces for the non-uniform linear subdivision: F = Xn−1 j=0 cjPj , (3) where cj , j = 0, . . . , n − 1 are unknown weights. Then after one dual step on the linearly refined control mesh, we obtain a vertex refinement rule Pi = 1 4 (Pi + Ei−1 + Ei + F) = 1 4 (1 + ci + qi+1 pi + qi+1 + pi−1 pi−1 + qi )Pi + 1 4 X |i−j|>1 cjPj + 1 4 (ci−1 + qi pi−1 + qi )Pi−1 + 1 4 (ci+1 + pi pi + qi+1 )Pi+1. (4) Here we let pi = d 0 i,i+1 and qi = d 0 i,i−1 for the sake of simplicity. That is to say that for a vertex of a face, the corresponding new vertex is the average of four points: the vertex, two edge points on the edges incident on this vertex in the face, and the face point of the face. In both the Catmull-Clark variant of Doo-Sabin subdivision and non-uniform biquadratic B-spline subdivision, face points are the (weighted) centroids of the corresponding faces and ap￾pear on the limit surface, namely, face points are the limit points corresponding to the centers of the faces. Requiring the rule of Eq. (3) possesses the same property, we have F = Xn−1 j=0 cjPj = Xn−1 j=0 cjPj . With the aid of a computer algebra system such as Mathemat￾ica, by solving a system of linear equations with respect to 4