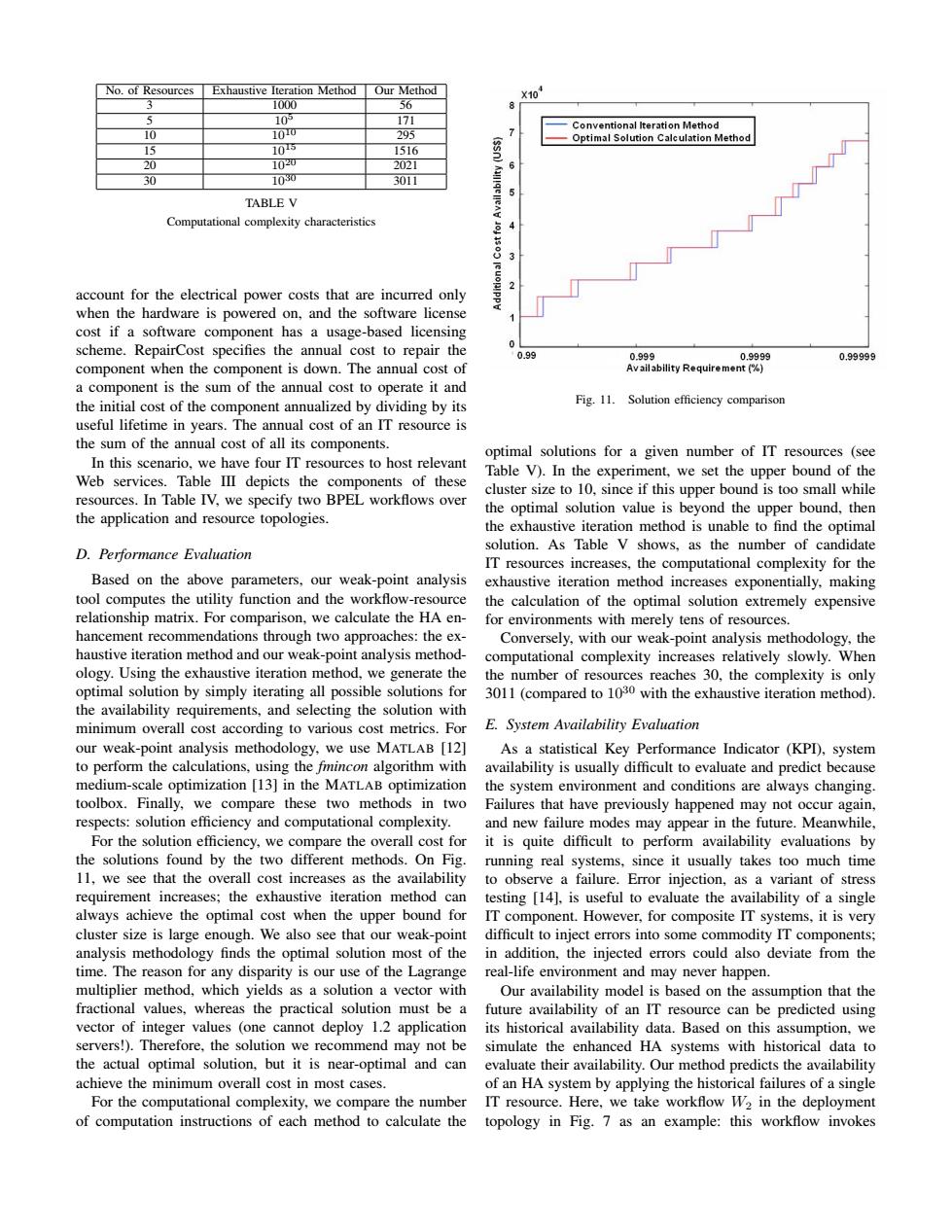
No.of Resources Exhaustive Iteration Method Our Method X10 1000 56 10时 171 Conventional Iteration Method 10 100 295 7 Optimal Solution Calculation Method 15 105 1516 20 1020 2021 30 1030 3011 TABLE V Computational complexity characteristics 2 account for the electrical power costs that are incurred only when the hardware is powered on,and the software license cost if a software component has a usage-based licensing scheme.RepairCost specifies the annual cost to repair the 0.99 099A 0.9999 0.99999 component when the component is down.The annual cost of Avail ability Require ment(%) a component is the sum of the annual cost to operate it and the initial cost of the component annualized by dividing by its Fig.11.Solution efficiency comparison useful lifetime in years.The annual cost of an IT resource is the sum of the annual cost of all its components optimal solutions for a given number of IT resources (see In this scenario,we have four IT resources to host relevant Web services.Table III depicts the components of these Table V).In the experiment,we set the upper bound of the cluster size to 10,since if this upper bound is too small while resources.In Table IV,we specify two BPEL workflows over the optimal solution value is beyond the upper bound,then the application and resource topologies. the exhaustive iteration method is unable to find the optimal D.Performance Evaluation solution.As Table V shows,as the number of candidate IT resources increases,the computational complexity for the Based on the above parameters,our weak-point analysis exhaustive iteration method increases exponentially,making tool computes the utility function and the workflow-resource the calculation of the optimal solution extremely expensive relationship matrix.For comparison,we calculate the HA en- for environments with merely tens of resources. hancement recommendations through two approaches:the ex- Conversely,with our weak-point analysis methodology,the haustive iteration method and our weak-point analysis method- computational complexity increases relatively slowly.When ology.Using the exhaustive iteration method,we generate the the number of resources reaches 30,the complexity is only optimal solution by simply iterating all possible solutions for 3011(compared to 1030 with the exhaustive iteration method). the availability requirements,and selecting the solution with minimum overall cost according to various cost metrics.For E.System Availability Evaluation our weak-point analysis methodology,we use MATLAB [12] As a statistical Key Performance Indicator (KPD),system to perform the calculations,using the finincon algorithm with availability is usually difficult to evaluate and predict because medium-scale optimization [13]in the MATLAB optimization the system environment and conditions are always changing. toolbox.Finally,we compare these two methods in two Failures that have previously happened may not occur again, respects:solution efficiency and computational complexity. and new failure modes may appear in the future.Meanwhile, For the solution efficiency,we compare the overall cost for it is quite difficult to perform availability evaluations by the solutions found by the two different methods.On Fig.running real systems,since it usually takes too much time 11,we see that the overall cost increases as the availability to observe a failure.Error injection,as a variant of stress requirement increases;the exhaustive iteration method can testing [14].is useful to evaluate the availability of a single always achieve the optimal cost when the upper bound for IT component.However,for composite IT systems,it is very cluster size is large enough.We also see that our weak-point difficult to inject errors into some commodity IT components; analysis methodology finds the optimal solution most of the in addition,the injected errors could also deviate from the time.The reason for any disparity is our use of the Lagrange real-life environment and may never happen. multiplier method,which yields as a solution a vector with Our availability model is based on the assumption that the fractional values,whereas the practical solution must be a future availability of an IT resource can be predicted using vector of integer values (one cannot deploy 1.2 application its historical availability data.Based on this assumption,we servers!).Therefore,the solution we recommend may not be simulate the enhanced HA systems with historical data to the actual optimal solution,but it is near-optimal and can evaluate their availability.Our method predicts the availability achieve the minimum overall cost in most cases. of an HA system by applying the historical failures of a single For the computational complexity,we compare the number IT resource.Here,we take workflow W2 in the deployment of computation instructions of each method to calculate the topology in Fig.7 as an example:this workflow invokesNo. of Resources Exhaustive Iteration Method Our Method 3 1000 56 5 105 171 10 1010 295 15 1015 1516 20 1020 2021 30 1030 3011 TABLE V Computational complexity characteristics account for the electrical power costs that are incurred only when the hardware is powered on, and the software license cost if a software component has a usage-based licensing scheme. RepairCost specifies the annual cost to repair the component when the component is down. The annual cost of a component is the sum of the annual cost to operate it and the initial cost of the component annualized by dividing by its useful lifetime in years. The annual cost of an IT resource is the sum of the annual cost of all its components. In this scenario, we have four IT resources to host relevant Web services. Table III depicts the components of these resources. In Table IV, we specify two BPEL workflows over the application and resource topologies. D. Performance Evaluation Based on the above parameters, our weak-point analysis tool computes the utility function and the workflow-resource relationship matrix. For comparison, we calculate the HA en￾hancement recommendations through two approaches: the ex￾haustive iteration method and our weak-point analysis method￾ology. Using the exhaustive iteration method, we generate the optimal solution by simply iterating all possible solutions for the availability requirements, and selecting the solution with minimum overall cost according to various cost metrics. For our weak-point analysis methodology, we use MATLAB [12] to perform the calculations, using the fmincon algorithm with medium-scale optimization [13] in the MATLAB optimization toolbox. Finally, we compare these two methods in two respects: solution efficiency and computational complexity. For the solution efficiency, we compare the overall cost for the solutions found by the two different methods. On Fig. 11, we see that the overall cost increases as the availability requirement increases; the exhaustive iteration method can always achieve the optimal cost when the upper bound for cluster size is large enough. We also see that our weak-point analysis methodology finds the optimal solution most of the time. The reason for any disparity is our use of the Lagrange multiplier method, which yields as a solution a vector with fractional values, whereas the practical solution must be a vector of integer values (one cannot deploy 1.2 application servers!). Therefore, the solution we recommend may not be the actual optimal solution, but it is near-optimal and can achieve the minimum overall cost in most cases. For the computational complexity, we compare the number of computation instructions of each method to calculate the Fig. 11. Solution efficiency comparison optimal solutions for a given number of IT resources (see Table V). In the experiment, we set the upper bound of the cluster size to 10, since if this upper bound is too small while the optimal solution value is beyond the upper bound, then the exhaustive iteration method is unable to find the optimal solution. As Table V shows, as the number of candidate IT resources increases, the computational complexity for the exhaustive iteration method increases exponentially, making the calculation of the optimal solution extremely expensive for environments with merely tens of resources. Conversely, with our weak-point analysis methodology, the computational complexity increases relatively slowly. When the number of resources reaches 30, the complexity is only 3011 (compared to 1030 with the exhaustive iteration method). E. System Availability Evaluation As a statistical Key Performance Indicator (KPI), system availability is usually difficult to evaluate and predict because the system environment and conditions are always changing. Failures that have previously happened may not occur again, and new failure modes may appear in the future. Meanwhile, it is quite difficult to perform availability evaluations by running real systems, since it usually takes too much time to observe a failure. Error injection, as a variant of stress testing [14], is useful to evaluate the availability of a single IT component. However, for composite IT systems, it is very difficult to inject errors into some commodity IT components; in addition, the injected errors could also deviate from the real-life environment and may never happen. Our availability model is based on the assumption that the future availability of an IT resource can be predicted using its historical availability data. Based on this assumption, we simulate the enhanced HA systems with historical data to evaluate their availability. Our method predicts the availability of an HA system by applying the historical failures of a single IT resource. Here, we take workflow W2 in the deployment topology in Fig. 7 as an example: this workflow invokes