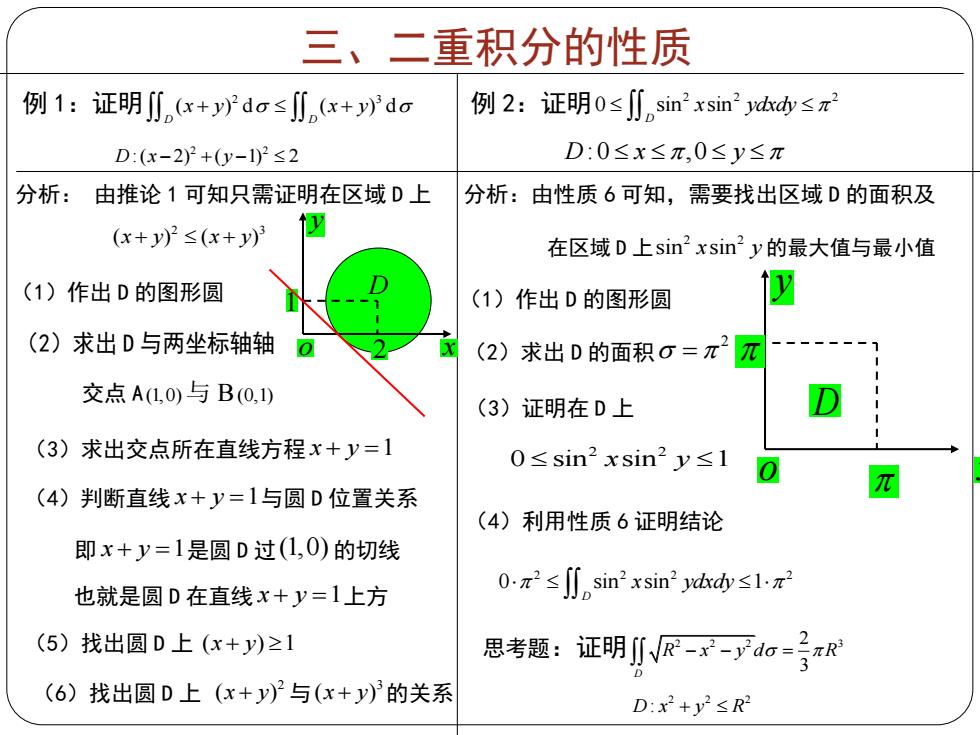
三、二重积分的性质 例1：证明，x+ydo≤∬n(x+yda 例2：证明0≤∬nsin2xsin2dkd≤元2 D:(x-22+0y-102≤2 D:0≤x≤π，0≤y≤π 分析： 由推论1可知只需证明在区域D上 分析：由性质6可知，需要找出区域D的面积及 (x+y)2≤(x+y) 在区域D上sin2xsin2y的最大值与最小值 (1)作出D的图形圆 (1)作出D的图形圆 極 (2)求出D与两坐标轴轴 0 (2) 求出D的面积0=π2元 交点A(L,0)与B0,) (3)证明在D上 D (3)求出交点所在直线方程x+y=1 0≤sin2xsin2y≤l 0 (4)判断直线x+y=1与圆D位置关系 π (4)利用性质6证明结论 即x+y=1是圆D过(L,0)的切线 也就是圆D在直线x+y=1上方 0:x2≤J∬nsin2xsin2d≤1x (5)找出圆D上(x+y)≥1 2 思考题：证明川R-x-ydo= (6)找出圆D上(x+y)与(x+y)3的关系 D:x2+y2≤R2 三、二重积分的性质 例 1：证明 2 3 ( ) d ( ) d D D x y x y        2 2 D x y :( 2) ( 1) 2     例 2：证明 2 2 2 0 sin sin D   x ydxdy   D x y :0 ,0       y o 2 x 1 D 分析： 由推论 1 可知只需证明在区域 D 上 2 3 ( ) ( ) x y x y    （1）作出 D 的图形圆 （2）求出 D 与两坐标轴轴 交点 A(1,0)与 B(0,1) （3）求出交点所在直线方程 x y  1 （4）判断直线 x y  1与圆 D 位置关系 即 x y  1是圆 D 过(1,0) 的切线 也就是圆 D 在直线 x y  1上方 （5）找出圆 D 上 ( ) 1 x y   （6）找出圆 D 上 2 ( ) x y  与 3 ( ) x y  的关系 分析：由性质 6 可知，需要找出区域 D 的面积及 在区域 D 上 2 2 sin sin x y 的最大值与最小值 （1）作出 D 的图形圆 （2）求出 D 的面积 2    （3）证明在 D 上 2 2 0 sin sin 1   x y （4）利用性质 6 证明结论 y  o x D  2 2 2 2 0 sin sin 1 D       x ydxdy  思考题：证明 2 2 2 3 2 3 D R x y d R       2 2 2 D x y R :  