第九章重积分及曲线积分 二重积分及应用 主要内容 三重积分及应用 曲线积分 曲面积分
二重积分及应用 三重积分及应用 曲线积分 主 要 内 容 曲面积分 第九章 重积分及曲线积分
§9.1二重积分的概念及性质 概念产生的背景 二重积分的概念 主要内容 二重积分的性质 二重积分性质的应用
概念产生的背景 二重积分的概念 二重积分的性质 二重积分性质的应用 主 要 内 容 §9.1 二重积分的概念及性质
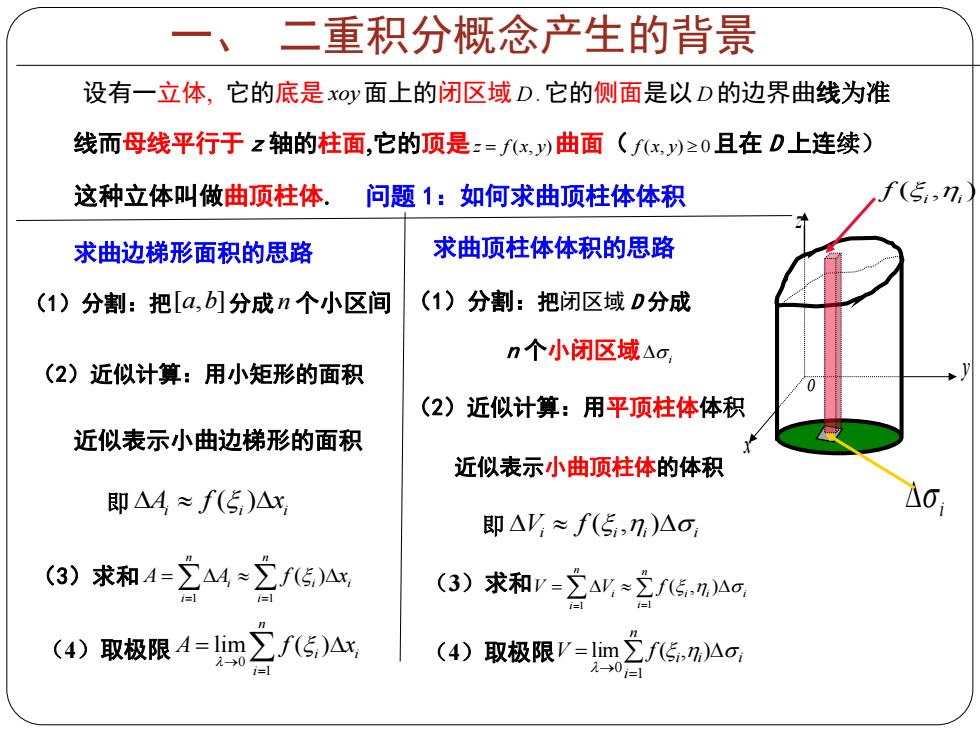
一、二重积分概念产生的背景 设有一立体,它的底是x0y面上的闭区域D.它的侧面是以D的边界曲线为准 线而母线平行于z轴的柱面,它的顶是:=fx,)曲面(fx,)≥0且在D上连续) 这种立体叫做曲顶柱体。问题1:如何求曲顶柱体体积 (5,7,》 求曲边梯形面积的思路 求曲顶柱体体积的思路 (1)分割:把[a,b]分成n个小区间 (1)分割:把闭区域D分成 n个小闭区域△a (2)近似计算:用小矩形的面积 (2)近似计算:用平顶柱体体积 近似表示小曲边梯形的面积 近似表示小曲顶柱体的体积 即A4≈f(5)△x 即△V,≈f(5,7)△ (3) 求和A=2AM∑f5)Ax (3)求和r-2a业2.na (4) 取极限A=lim∑f传)△x (4) 元0 取极限V=m2f传△a, 201
设有一立体 它的底是 xoy面上的闭区域D .它的侧面是以D的边界曲线为准 线而母线平行于 z 轴的柱面它的顶是z f x y ( , )曲面( f x y ( , ) 0 且在 D 上连续) 这种立体叫做曲顶柱体 x z y o D 问题 1:如何求曲顶柱体体积 求曲边梯形面积的思路 (1)分割:把[ , ] a b 分成 n 个小区间 (2)近似计算:用小矩形的面积 近似表示小曲边梯形的面积 即 ( ) A f x i i i (3)求和 1 1 ( ) n n i i i i i A A f x (4)取极限 0 1 lim ( ) n i i i A f x (1)分割:把闭区域 D 分成 n 个小闭区域 i (2)近似计算:用平顶柱体体积 近似表示小曲顶柱体的体积 即 ( , ) V f i i i i (3)求和 1 1 ( , ) n n i i i i i i V V f 求曲顶柱体体积的思路 i ( , ) i i f (4)取极限 i i i n i V f lim ( , ) 1 0 一、 二重积分概念产生的背景
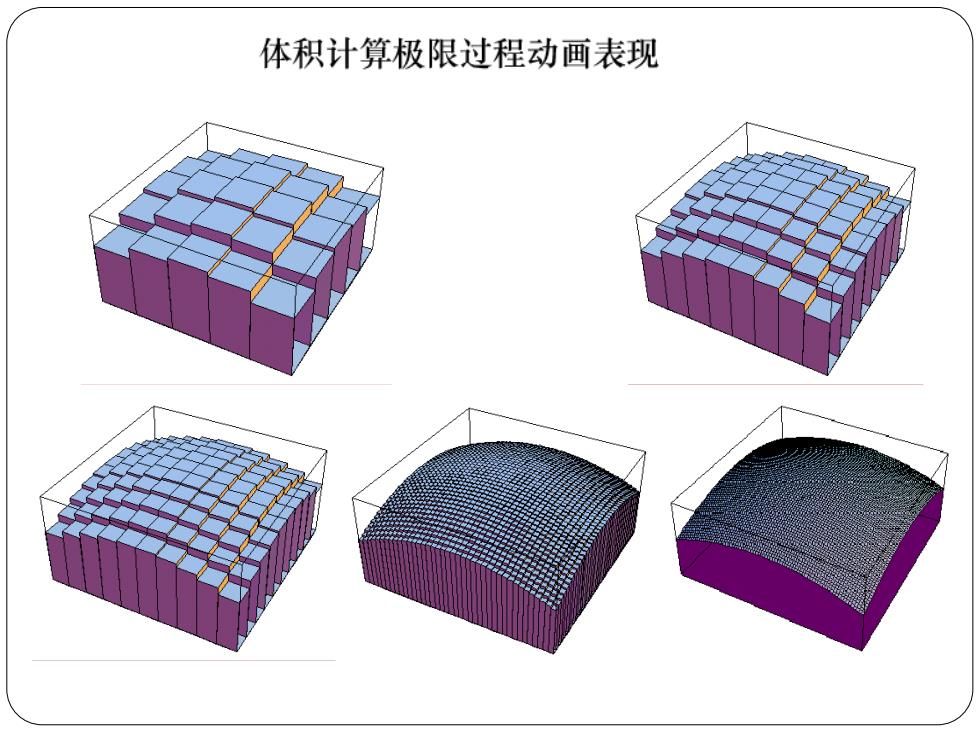
体积计算极限过程动画表现

二、二重积分的概念 1.二重积分的定义 设fx,y)是有界闭区域D上的有界函数. (1)将闭区域D任意分成n个小闭区域△o,△o2,,△on其中△o,表示第i个小区域 也表示它的面积. (2)在每个Ag,上任取-点(5,),作乘积f,n)△a,并作和2/怎,)Aa. I- (3)如果当无限增大且各小闭区域的直径中的最大值入趋于零时,这和的极限总存在 则称此极限为函数f(x,y)在闭区域D上的二重积分,记作∬xo,即 D 即 f(x.yxlo-lim2f(m)Aa, D →01 D f(x,y) x,y f(x,y)do do f(.)Ac, 1=1 积分区域 被积函数 积分变量 被积表达式 面积元素 积分和
1. 二重积分的定义 设 f x y ( , )是有界闭区域 D 上的有界函数 (1)将闭区域 D 任意分成 n 个小闭区域 1 2, n 其中 i表示第 i 个小区域 也表示它的面积 (2)在每个 i上任取一点( i i) 作乘积 ( , ) , i i i f 并作和 i i i n i f ( , ) 1 (3)如果当n 无限增大且各小闭区域的直径中的最大值 趋于零时 这和的极限总存在 则称此极限为函数 f x y ( , )在闭区域 D 上的二重积分 记作 f x y d D ( , ) 即 即 i i i n D i f x y d f ( , ) lim ( , ) 1 0 D 积分区域 f x y ( , ) 被积函数 x y, 积分变量 f x y d ( , ) 被积表达式 d 面积元素 1 ( , ) n i i i i f 积分和 二、 二重积分的概念

二、二重积分的概念 注记1:二重积分fx,o仅与被积函数和积分 注记2二重积分的几何意义 区域有关与区域D的分法及点的选择 (1)如果f(x,)≥0,二重积分川fxo 就是曲顶柱体的体积」 无关 (2)如果fx,)<0,二重积分∬fxo 就是曲顶柱体的体积的负值. (3)如果f(x,y)在D的若干部分是正的 在其余部分是负的,那么f(x,y)在 因此在直角坐标系中,有时也把面积元素do D上的二重积分等于xOy面上方的曲 记作kd山而把二重积分记作∬fx,yk山. 顶柱体体积减去xOy面下方的曲顶柱 注记3:当f(x,y)在闭区域D上连续时 函数fx,)在D上的二重积分必定存在. 体体积的所得的差
注记 1:二重积分 f x y d D ( , ) 仅与被积函数和积分 区域有关与区域 D 的分法及点的选择 无关. 因此在直角坐标系中 有时也把面积元素 d 记作dxdy 而把二重积分记作 f x y dxdy D ( , ) . x y o D 注记 3: 当 f x y ( , )在闭区域 D 上连续时 函数 f x y ( , )在 D 上的二重积分必定存在 注记 2 二重积分的几何意义 (1)如果 f x y ( , ) 0 ,二重积分 f x y d D ( , ) 就是曲顶柱体的体积 (2)如果 f x y ( , ) 0 ,二重积分 f x y d D ( , ) 就是曲顶柱体的体积的负值 (3)如果 f x y ( , )在 D 的若干部分是正的 在其余部分是负的 那么 f (x, y)在 D 上的二重积分等于 xoy面上方的曲 顶柱体体积减去 xoy面下方的曲顶柱 体体积的所得的差. 二、 二重积分的概念

二重积分与一元函数的定积分的比较 二重积分的概念是一元函数定积分概念的推广(都是积分和的极限) 1.二重积分的积分符号是表示 定积分的积分符号用一个表示 2.二重积分的积分区域是平面上的一个闭区域 定积分的积分区间是数轴上的一个闭区间 3.二重积分的积分函数是一个二元函数 定积分的积分函数是一个一元函数 4.二重积分的积分变量有两个 定积分的积分变量有一个 5.二重积分的绝对值是一个曲顶柱体的体积 定积分的绝对值是一个曲边梯形的面积
二重积分的概念是一元函数定积分概念的推广(都是积分和的极限) 1. 二重积分的积分符号是 表示 定积分的积分符号用一个 表示 2. 二重积分的积分区域是平面上的一个闭区域 定积分的积分区间是数轴上的一个闭区间 3. 二重积分的积分函数是一个二元函数 定积分的积分函数是一个一元函数 4. 二重积分的积分变量有两个 定积分的积分变量有一个 5. 二重积分的绝对值是一个曲顶柱体的体积 定积分的绝对值是一个曲边梯形的面积 二重积分与一元函数的定积分的比较

三、二重积分的性质 类比定积分的性质 二重积分的性质 性质1: 心f)d=kf6)杰 性质1:∬xo=fx,o 性质2:心U)+gxk=心fk+心gd 性质2: Ux,n+8o-∬fyao+∬sxa 性质3(积分区间的可加性) 性质3(积分区域的可加性)如果积分区域D分为两个 (x=d+ds 闭区域A与B,则∬fco=∬fxo+∬fx,o 0 性质4 f1dk=b-a 性质4 o-=go为的西积, 性质5(定积分的保号性)如果在区间[a,]上 性质5(保号性)如果在区域D上,fx,)≥0 fx)≥0,则fx)d≥0 则 J∬fx,y)dG≥0 推论1 如果在区间[a,b1上,fx)≤g(x) 推论1 如果在闭区域D上,fx,)≤g(x,y) 则f≤∫心gwd 则∬fx,yda≤川gx,do 推论2 rd ss 推论2 fx,ydos∬fx,yldo
类比定积分的性质 二重积分的性质 性质 1: kf x dx b a ( ) k f x dx b a ( ) 性质 1: kf x y d k f x y d D D ( , ) ( , ) 性质 2: f x g x dx f x dx g x dx b a b a b a ( ) ( ) ( ) ( ) : 性质 2: f x y g x y d f x y d g x y d D D D [ ( , ) ( , )] ( , ) ( , ) 性质 3 (积分区间的可加性) 性质 3 (积分区域的可加性)如果积分区域 D 分为两个 闭区域 D1与 D2 则 f x y d f x y d f x y d D D D 1 2 dx ( , ) ( , ) ( , ) f x dx f x dx f x b c c a b a ( ) ( ) ( ) 性质 4 1 b a dx b a 性质 4 D D 1 d d ( 为 D 的面积) 性质 5 (定积分的保号性) 如果在区间[a,b]上 f x( ) 0 ,则 ( ) 0 f x dx b a 性质 5 (保号性)如果在区域D上, f x y ( , ) 0 则 ( , ) 0 D f x y d 推论 1 如果在区间[a,b]上, f x g x ( ) ( ) 则 ( ) ( ) b b a a f x dx g x dx 推论 1 如果在闭区域D上, f x y g x y ( , ) ( , ) 则 ( , ) ( , ) D D f x y d g x y d 推论 2 f x dx f x dx b a b a ( ) ( ) 推论 2 ( , ) ( , ) D D f x y d f x y d 三、二重积分的性质

三、二重积分的性质 类比定积分的性质 二重积分的性质 性质6 如果m,M是函数fx)在区间a,b]上性质6如果m,M是函数f(x,)在闭区域D上 最小值和最大值,则 最小值和最大值,则 mb-a)≤fe)k≤M6-a). mo≤∬fx,y)do≤Mo,其中,o为D的面积. 性质7(积分中值定理)如果函数fx)在性质7(积分中值定理)如果函数fx,y)在 积分区间[a,b1上连续 闭区域D上连续,σ为D的 则在[a,1上至少存在一个点使得 面积则在D上至少存在一个点(5,)使得 ∫心fx)=f5b-a) .yda-.a
类比定积分的性质 二重积分的性质 性质 6 如果m M, 是函数 f x( )在区间[a,b]上 最小值和最大值,则 m b a f x dx M b a a b b a ( ) ( ) ( ), 性质 6 如果m M, 是函数 f x y ( , )在闭区域D上 最小值和最大值,则 m f (x, y)d M, D 其中, 为 D 的面积 性质 7 (积分中值定理)如果函数 f (x)在 积分区间[a,b]上连续 则在[a,b]上至少存在一个点 使得 f (x)dx f ( )(b a) b a 性质 7 (积分中值定理)如果函数 f x y ( , )在 闭区域D上连续, 为 D 的 面积则在 D 上至少存在一个点(,)使得 ( , ) ( , ) D f x y d f 三、二重积分的性质
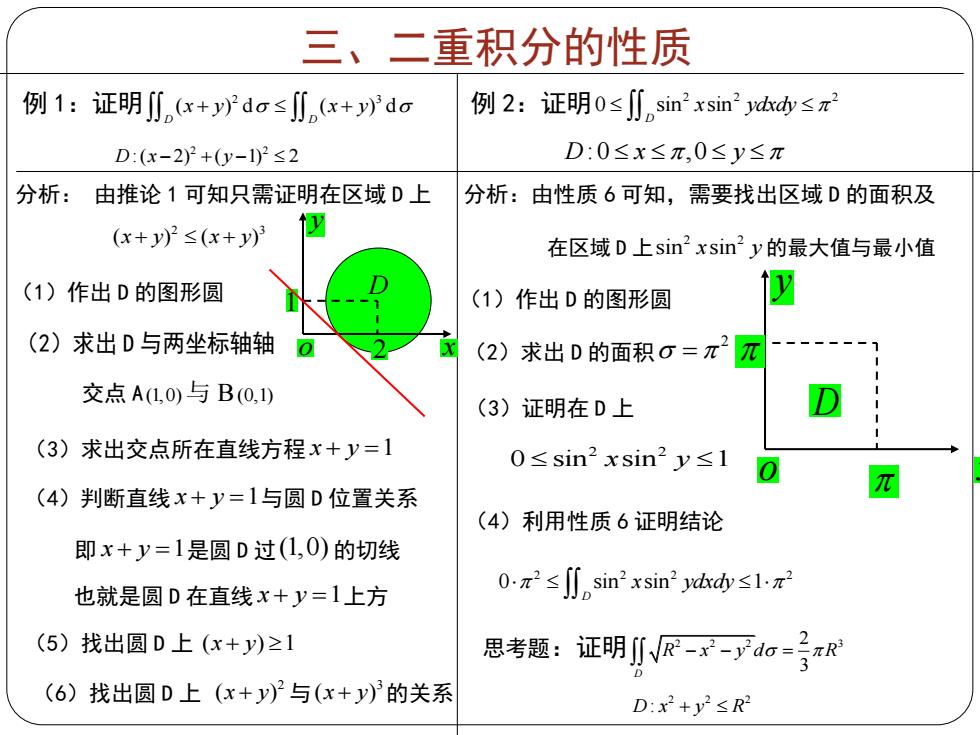
三、二重积分的性质 例1:证明,x+ydo≤∬n(x+yda 例2:证明0≤∬nsin2xsin2dkd≤元2 D:(x-22+0y-102≤2 D:0≤x≤π,0≤y≤π 分析: 由推论1可知只需证明在区域D上 分析:由性质6可知,需要找出区域D的面积及 (x+y)2≤(x+y) 在区域D上sin2xsin2y的最大值与最小值 (1)作出D的图形圆 (1)作出D的图形圆 極 (2)求出D与两坐标轴轴 0 (2) 求出D的面积0=π2元 交点A(L,0)与B0,) (3)证明在D上 D (3)求出交点所在直线方程x+y=1 0≤sin2xsin2y≤l 0 (4)判断直线x+y=1与圆D位置关系 π (4)利用性质6证明结论 即x+y=1是圆D过(L,0)的切线 也就是圆D在直线x+y=1上方 0:x2≤J∬nsin2xsin2d≤1x (5)找出圆D上(x+y)≥1 2 思考题:证明川R-x-ydo= (6)找出圆D上(x+y)与(x+y)3的关系 D:x2+y2≤R2
三、二重积分的性质 例 1:证明 2 3 ( ) d ( ) d D D x y x y 2 2 D x y :( 2) ( 1) 2 例 2:证明 2 2 2 0 sin sin D x ydxdy D x y :0 ,0 y o 2 x 1 D 分析: 由推论 1 可知只需证明在区域 D 上 2 3 ( ) ( ) x y x y (1)作出 D 的图形圆 (2)求出 D 与两坐标轴轴 交点 A(1,0)与 B(0,1) (3)求出交点所在直线方程 x y 1 (4)判断直线 x y 1与圆 D 位置关系 即 x y 1是圆 D 过(1,0) 的切线 也就是圆 D 在直线 x y 1上方 (5)找出圆 D 上 ( ) 1 x y (6)找出圆 D 上 2 ( ) x y 与 3 ( ) x y 的关系 分析:由性质 6 可知,需要找出区域 D 的面积及 在区域 D 上 2 2 sin sin x y 的最大值与最小值 (1)作出 D 的图形圆 (2)求出 D 的面积 2 (3)证明在 D 上 2 2 0 sin sin 1 x y (4)利用性质 6 证明结论 y o x D 2 2 2 2 0 sin sin 1 D x ydxdy 思考题:证明 2 2 2 3 2 3 D R x y d R 2 2 2 D x y R :