南阳师范学院：《高等数学》课程教学资源（课件讲稿）10.3 幂级数

§10.3 幂级数 函数项级数的概念 幂级数及收敛区间 幂级数的运算

§10.3 幂级数 函数项级数的概念 幂级数及收敛区间 幂级数的运算

函数项级数及其有关的概念 函数项级数的概念 函数项级数的收敛域 给定一个定义在区间I上的函数列 o∈I ∑4(x)收敛 (x)发散 4(x),山2(x),…,山n(x),…,则式子 4(x)+4(x)+…+un(x)+… x称为 xo称为 收敛点 发散点 称为区间I上的函数项级数，记作 ∑u.( 即 ∑4，()=4(x)+4,()+…+,(x)+. =1+++ 函数项级数“， 函数项级数u,(x) n=1 如 n=1 所有收敛点集合 所有发散点集合 显然r 称为收敛域 称为发散域 的收敛域为(-1,1) n=1

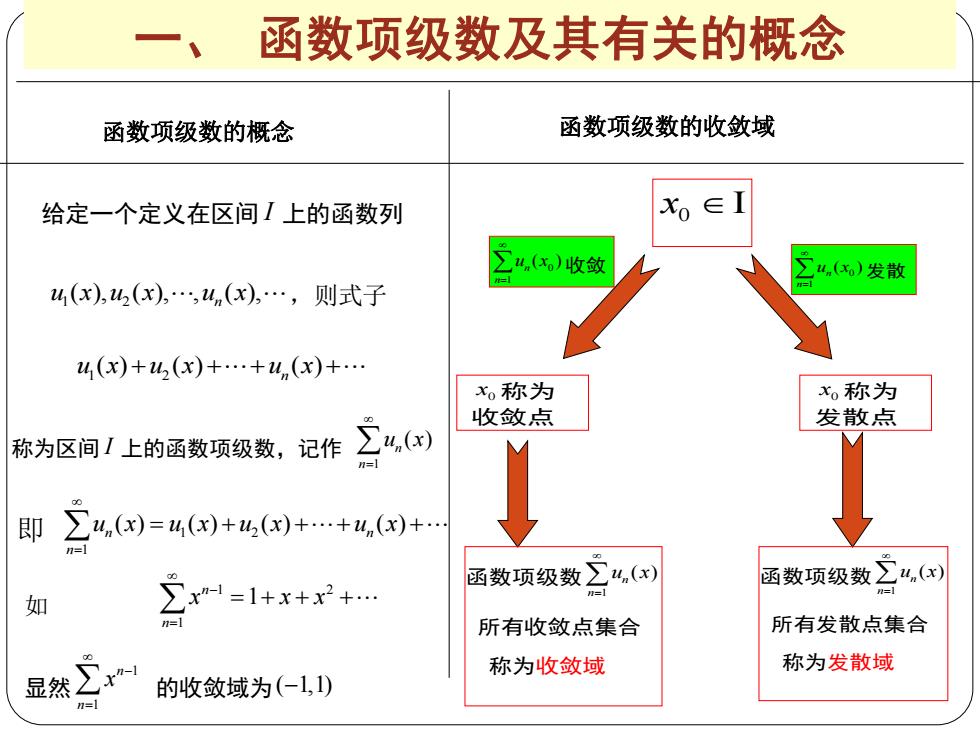
一、 函数项级数及其有关的概念 函数项级数的概念 函数项级数的收敛域 给定一个定义在区间 I 上的函数列 1 2 ( ), ( ), , ( ), n u x u x u x  ，则式子 1 2 ( ) ( ) ( ) u x u x u x    n 称为区间 I 上的函数项级数，记作 1 ( ) n n u x    即 1 2 1 ( ) ( ) ( ) ( ) n n n u x u x u x u x         如 1 2 1 1 n n x x x          0 x 0 1 ( ) n n u x    收敛 x0 称为 收敛点 0 1 ( ) n n u x    发散 x0 称为 发散点 函数项级数 1 ( ) n n u x    所有收敛点集合 称为收敛域 函数项级数 1 ( ) n n u x    所有发散点集合 称为发散域 显然 1 1 n n x     的收敛域为( 1,1) 

二 幂级数及收敛域 幂级数的概念 幂级数的收敛域 上a-称为的幂级数 定理1：幂级数，x:的收敛性为下列三种情形之一 (1)在(-0，+∞)内处处绝对收敛 41,42,…,an…称为幂级数 (称它的收敛半径R=+0,(-∞，+∞)是它的收敛域) 的系数，是常数 2)仅在x=0处收敛； 当。=0时， 称为x的幂级数 (称它的收敛半径R=0,它的收敛域为一个点x=0 (3)存在确定的正数R,当R时发散. 就转化为幂级数a (称它的收敛半径为R,收敛区间为（一R,R), 收敛域为四种之一：(-RR),(←R,R,-R,R),[一RR]

二、 幂级数及收敛域 幂级数的概念 幂级数的收敛域  0  0 n n n a x x     称为( ) 0 x  x 的幂级数 1 2 , , , n a a a   称为幂级数 的系数，是常数 当 0 x0  时， 0 n n n a x    称为 x 的幂级数. 令 0 t x x   时，幂级数  0  0 n n n a x x     就转化为幂级数 0 n n n a t    定理 1：幂级数 0 n n n a x    :的收敛性为下列三种情形之一： （1）在(,)内处处绝对收敛 （称它的收敛半径 R   ，(,) 是它的收敛域） （2）仅在 x  0处收敛； （称它的收敛半径R  0，它的收敛域为一个点 x  0） （3）存在确定的正数 R ，当 x R  时绝对收敛， 当 x R  时发散. （称它的收敛半径为 R ，收敛区间为( , ) R R ， 收敛域为四种之一：( , ), R R ( , ], R R [ , ), R R [ , ] R R

二 幂级数及收敛域 定理2 设幂级数∑a,r的系数满足 例1 求幂级数-)的收敛半径和收敛域 n=0 lim an*l上p 解 显然a=(-1) n-c0 an n 1 则这幂级数的收敛半径 因此 im卡limn+=l a. 1 D=0 所以p=1,故收敛半径为R==1 P≠0 0 p=+∞ 当x=1时，幂级数成为2-是收敛的 第一步：确定幂级数a,r的系数通项a 当x=-1时，幂级数成为是发散的 第二步：计算极限P 因此，幂级数立-1)的收敛域为-1,1]. 第三步：确定2ar的收敛半径 = 第四步： 确定三x的收敛域

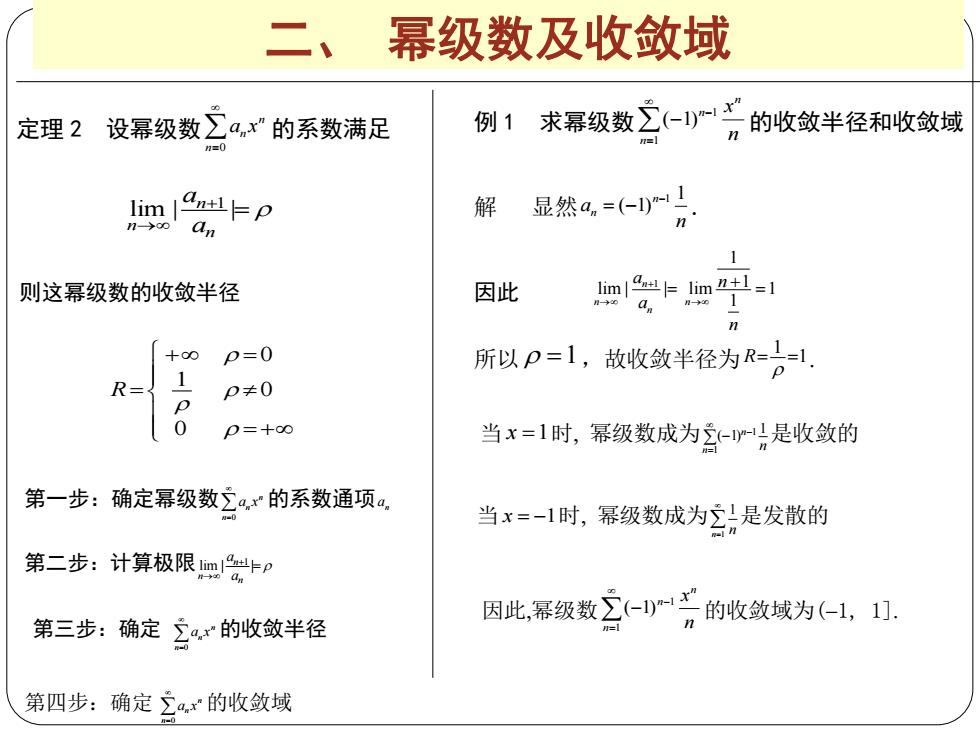
二、 幂级数及收敛域 定理 2 设幂级数 0 n n n a x    的系数满足     lim | | 1 n n n a a 则这幂级数的收敛半径                0 0 1 0 R 例 1 求幂级数 1 1 ( 1) n n n x n      的收敛半径和收敛域 第一步：确定幂级数 0 n n n a x    的系数通项 n a 第二步：计算极限     lim | | 1 n n n a a 第三步：确定 0 n n n a x    的收敛半径 第四步：确定 0 n n n a x    的收敛域 解 显然 1 1 ( 1)n n a n    . 因此 1 1 1 lim | | lim 1 1 n n n n a n a n       所以  1，故收敛半径为 1 1    R  当 x 1时 幂级数成为     1 1 1 ( 1) n n n 是收敛的 当 x  1时 幂级数成为 1 1 n n    是发散的 因此幂级数 1 1 ( 1) n n n x n      的收敛域为(1, 1]

二 幂级数及收敛域 定理2 设幂级数 r的系数满足 例2 求幂级数三 的收敛半径和收敛域 lim卡p 解 1n-→c0 an 显然a,=m 1 则这幂级数的收敛半径 因此 lmu卡limm+=lim1 =0 月→ a i-→on+1 n! +00 p=0 p≠0 所以p=0,故收敛半径为R=0. P D=+0 第一步：确定幂级数4，x的系数通项a, 因此，幂级数的收敛域为(-o,+o), 第二步：计算极限mp 第三步：确定2ar的收敛半径 第四步：确定ar的收敛域

二、 幂级数及收敛域 定理 2 设幂级数 0 n n n a x    的系数满足     lim | | 1 n n n a a 则这幂级数的收敛半径                0 0 1 0 R 例 2 求幂级数 0 ! n n x n    的收敛半径和收敛域 第一步：确定幂级数 0 n n n a x    的系数通项 n a 第二步：计算极限     lim | | 1 n n n a a 第三步：确定 0 n n n a x    的收敛半径 第四步：确定 0 n n n a x    的收敛域 解 显然 1 ! n a n  . 因此 1 1 ( 1)! 1 lim | | lim lim 0 1 1 ! n n n n n a n a n n          所以   0，故收敛半径为 R  因此幂级数 0 ! n n x n    的收敛域为 ( , ).  

二 幂级数及收敛域 定理2 设幂级数∑a,的系数满足 例3求幂级数∑nl(x-l)的收敛域 =0 lim an 解令1=x-l,则幂级数空-y变为2r 则这幂级数的收敛半径 显然∑mlr 的通项系数an=n!. +0 p=0 因此 m12卡hma+少-n R 1 n! D≠0 0 p=+0 即p=+o.所以∑nlr的收敛半径为R=0 第一步： 确定幂级数a,r的系数通项。 第二步：计算极限m型p 从而级数2ar仅在1=0处收敛因此∑m(x- 第三步：确定 三0，r的收敛半径 仅在x=1处收敛. 第四步：确定 ∑ar的收敛域

二、 幂级数及收敛域 定理 2 设幂级数 0 n n n a x    的系数满足     lim | | 1 n n n a a 则这幂级数的收敛半径                0 0 1 0 R 例 3 求幂级数 1 !( 1)n n n x     的收敛域 第一步：确定幂级数 0 n n n a x    的系数通项 n a 第二步：计算极限     lim | | 1 n n n a a 第三步：确定 0 n n n a x    的收敛半径 第四步：确定 0 n n n a x    的收敛域 解 令 t x  1，则幂级数   0 ! 1 n n n x     变为 0 ! n n n t    显然 0 ! n n n t    的通项系数 ! n a n  . 因此 1 ( 1)! lim | | lim ! n n n n a n a n        即  .所以 0 ! n n n t    的收敛半径为 R  0 从而级数 0 ! n n n t    仅在t  0处收敛因此   0 ! 1 n n n x     仅在 x 1处收敛

二 幂级数及收敛域 例4求幂级敌器产的收敛区间 例4求器级数三器产的收敏区间 分析级数缺少奇次幂的项，定理2不能应用 解：幂级数的一般项记为4，)=2mx2.则 ()2 可根据比值审敛法来求收敛半径： 20n+10x2m+ limlimlim I( u (x) n-→∞un(x) 《)幂级数的一般项记为侧器产 m产 (2)计算1im 4n+1(x) 1=41x2 =lim (2n+22n+x2=41xP n-→0 (n+1)2 n-→o4n(x) 由比值审敛法可知： (3)利用比值审敛法判断x取何值时 当4|x2<1即1xk时级数收敛 当4|x?1即b号时级数发散 立u,(收敛、术取何值时疗4国发散、 所以器产收敛半径为号收敏城区间为

二、 幂级数及收敛域 例 4 求幂级数   0 2 2 ( !) (2 )! n n x n n 的收敛区间 解：幂级数的一般项记为 n n x n n u x 2 2 ( !) (2 )! ( ) 则 2( 1) 2 1 1 2 2 [2( 1)]! ( ) ( ) [( 1)!] lim | | lim lim ( ) ( ) (2 )! ( !) n n n n n n n n n n x u x u x n u x u x n x n           2 2 2 (2 2)(2 1) lim 4 | | ( 1) n n n x x  n      由比值审敛法可知： 当 4|x| 2 1 即 2 1 |x| 时级数收敛 当 4|x| 2 1 即 2 1 |x| 时级数发散 例 4 求幂级数   0 2 2 ( !) (2 )! n n x n n 的收敛区间 分析 级数缺少奇次幂的项 定理 2 不能应用 可根据比值审敛法来求收敛半径 （1）幂级数的一般项记为 n n x n n u x 2 2 ( !) (2 )! ( )  （2）计算 1 2 | 4| | ( ) ( ) lim | x u x u x n n n    （3）利用比值审敛法判断 x 取何值时 0 ( ) n n u x    收敛、 x 取何值时 0 ( ) n n u x    发散、 所以   0 2 2 ( !) (2 )! n n x n n 收敛半径为 2 1 R 收敛域区间为 1 1 , 2 2       

三 幂级数的运算及性质 幂级数的运算 幂级数的性质 设ar=KR6r=50,s()为2a,的和函数 = 则(1)s(x)在其收敛域内是连续.的 则 (2)s(x)在其收敛区间-R)内可导，且有逐项 交ar+9r-a线=0 求导公式 w-②ory-2ary-2ar 位arr)-a++ab+taA 求导后幂级数的收敛半径不变， (3)s(x)在其收敛区间(R)内有逐项积分公式 =S(x)S2(x) a0h=2orh=gorh=2r 其中 x<min(R,R) 积分后幂级数的收敛半径不变

三、 幂级数的运算及性质 幂级数的运算 幂级数的性质 设 0 n n n a x    1 1 2 2 0 ( ), ; ( ), n n n s x x R b x s x x R        则 1 2 0 0 0 ( ) ( ) ( ) n n n n n n n n n n a x b x a b x s x s x               0 0 0 0 0 ( )( ) ( ) n n n n n n k n k n n n n a x b x a b a b a b x               1 2  s x s x ( ) ( ) 性质：设   n0 n n a x 的收敛半径R  0, s x( ) 为   n0 n n a x 的和函数 则（1） s x( ) 在其收敛域内是连续的 （2） s x( ) 在其收敛区间( , ) R R 内可导，且有逐项 求导公式 1 0 0 1 ( ) ( ) ( ) n n n n n n n n n s x a x a x na x               求导后幂级数的收敛半径不变. （3） s x( ) 在其收敛区间( , ) R R 内有逐项积分公式 1 0 0 0 0 0 0 ( ) ( ) 1 x x x n n n n n n n n n a s t dt a t dt a t dt x n                  其中 min( , ) 1 2 x R R  积分后幂级数的收敛半径不变

三、幂级数的运算及性质 注 记 例5求幂级数∑(n+)x的和函数. (1)如果逐项微分或积分后的幂级数 解容易求得幂级数的收敛域为(-1,1). 当x=-R或x=R时收敛，则在x=-R 设和函数为)=2m+r心，xe(-L 或x=R处逐项微分和逐项积分公式 对上式从0到x积分可得 仍然成立. (2)如果a,在=-R或x=R时发散 0w-[2a+r]-2arw-2r- 则na,在x=-R或x=R时发敞 所以 - 两边求导可得 但2品”在一或=R时可能收敛 1 s(x)= 1- x∈(-1，) 也可能发散

三、 幂级数的运算及性质 注 记 （1）如果逐项微分或积分后的幂级数 当 x R   或 x R  时收敛则在 x R   或 x R  处逐项微分和逐项积分公式 仍然成立 （2）如果   n0 n n a x 在x R   或 x R  时发散 则 1 1 n n n na x     在x R  或 x R  时发散 但 1 0 1 n n n a x n      在x R  或 x R  时可能收敛 也可能发散 例 5 求幂级数 0 ( 1) n n n x     的和函数 解 容易求得幂级数的收敛域为（1 1) 设和函数为 0 ( ) ( 1) , ( 1,1) n n s x n x x        对上式从 0 到 x 积分可得 1 0 0 0 0 0 0 ( ) ( 1) ) ( 1) 1 x x x n n n n n n x s t dt n t dt n t dt x x                           所以 0 ( ) 1 x x s t dt x    两边求导可得   2 1 ( ) , 1 s x x   x ( 1,1)

三、幂级数的运算及性质 例6求幂级数x的收敛区间，并在收敛区间内求和函数， 2n-1 解令片”，则 则-2片j-2- lim =lim 因为 2-r,xe(-l10 故当|xk1时级数收敛，当x1时级数发散 所以 立-r,xe(-l,0 所以幂级数一的收敛半径为R=1 因此 x∈(-1,1) 收敛区间为(-1，) 故=0+s0h=1+7d 设 s)=-)4 xe(-L1) 2n-1 arctanx

三、 幂级数的运算及性质 例 6 求幂级数 1 2 1 1 ( 1) 2 1 n n n x n        的收敛区间，并在收敛区间内求和函数 解 令 1 2 1 ( 1) 2 1 n n n u x n      ，则 1 2 1 2 2 lim lim 2 1 n n n n u n x x u n        故当| | 1 x  时级数收敛，当| | 1 x  时级数发散. 所以幂级数 1 2 1 1 ( 1) 2 1 n n n x n        的收敛半径为R 1 收敛区间为( 1,1)  设 1 2 1 1 ( 1) ( ) 2 1 n n n s x x n         x ( 1,1) 则 1 2 1 1 ( 1) ( ) 2 1 n n n s x x n                 1 2( 1) 1 ( 1)n n n x         因为 1 1 1 1 ( 1) 1 n n n x x          x ( 1,1) 所以 1 2( 1) 2 1 1 ( 1) 1 n n n x x          x ( 1,1) 因此 2 1 ( ) 1 s x x    x ( 1,1) 故 2 0 0 1 ( ) (0) ( ) 1 x x s x s s t dt dt t         arctan x