§7.4平面及其方程 曲面方程 平面方程 两平面的 量平面的位 夹角 置关系
§7.4 平面及其方程 曲面方程 平面方程 两平面的 夹角 量平面的位 置关系

一 曲面方程 曲面在空间解析几何中被看成是点的几何轨迹 背景:求球心为M(x,,20)半径为 球心为原点半径为R的球面方程为 R的球面方程 x2+y2+z2=R2 解:设M(x,y,z)是球面上的任意点 (1)球面方程是一个关于x,八,2 则M(x,y,z)在球面上的充要条件是 的三元方程 (2)球面S上任一点的坐满足方程 MoM=R (x-x)}+(y-⅓)2+(2-)2=R2 即Vx-x)2+(y-)2+(z-2)2=R (3)满足方程x-+0-+-= 化简得(x-x)+(y-%)}+(2-)=R2 的点都在球面S上
一、曲面方程 曲面在空间解析几何中被看成是点的几何轨迹. 背景:求 球心为 ( , , ) 0 0 0 0 M x y z 半径为 R 的球面方程 解:设 M x y z ( , , )是球面上的任意点 则M x y z ( , , )在球面上的充要条件是 M M R 0 即 2 2 2 0 0 0 x x y y z z R 化简得 2 2 2 2 0 0 0 x x y y z z R (1)球面方程是一个关于 x y z , , 的三元方程 (2)球面S 上任一点的坐满足方程 2 2 2 2 0 0 0 x x y y z z R (3)满足方程 2 2 2 2 0 0 0 x x y y z z R 的点都在球面S 上 球心为原点半径为 R 的球面方程为 2 2 2 2 x y z R

一、 曲面方程 曲面方程 注记1:求曲面方程的步骤 如果曲面S与三元方程 第一步:建立适当的坐标系 F(x,y,z)=0 (1) 第二步:找出任意点在曲面上的 有下述关系: ①曲面S上任一点的坐标满足 充要条件 方程(); 第三步:用向量表示任意点在曲面上 ②满足方程(1)的点都在曲面S上 的充要条件 那么方程(1)就叫做曲面S的方程 第四步:化简 曲面S叫做方程()的图形
一、曲面方程 曲面方程 如果曲面 S 与三元方程 F x y z ( , , ) 0 (1) 有下述关系: ①曲面 S 上任一点的坐标满足 方程(1) ; ②满足方程(1) 的点都在曲面S 上 那么方程(1) 就叫做曲面S 的方程 曲面 S 叫做方程(1) 的图形. 注记1:求曲面方程的步骤 第一步:建立适当的坐标系 第二步:找出任意点在曲面上的 充要条件 第三步:用向量表示任意点在曲面上 的充要条件 第四步:化简
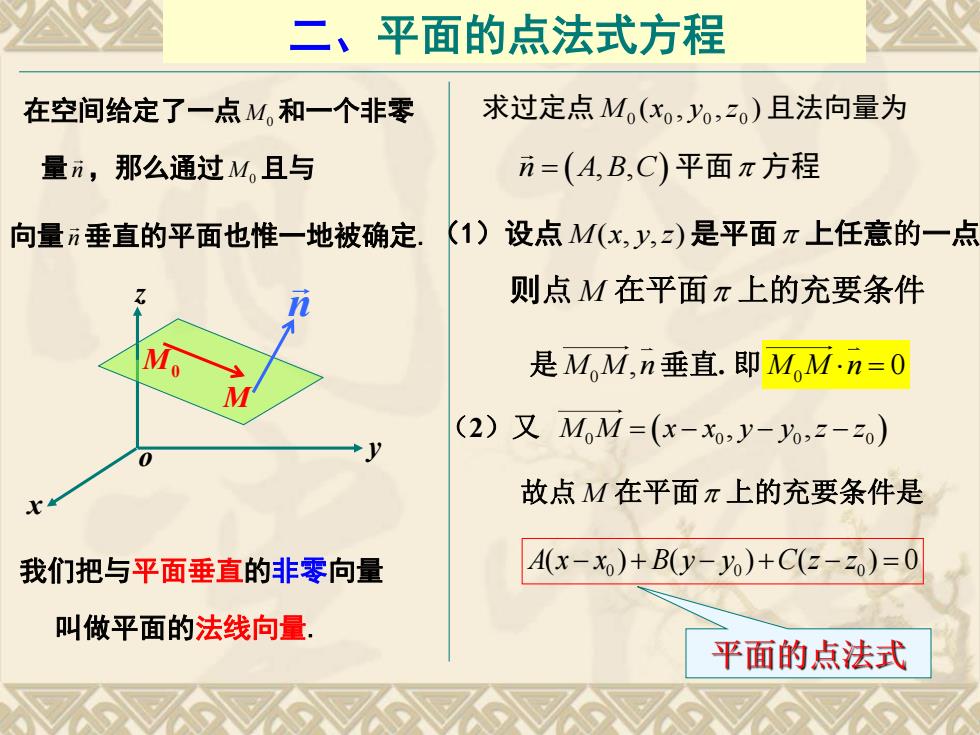
二、平面的点法式方程 在空间给定了一点M和一个非零 求过定点M(xo,y,二o)且法向量为 量n,那么通过M。且与 n=(A,B,C)平面π方程 向量垂直的平面也惟一地被确定。 (1)设点M(x,y,z)是平面π上任意的一点 则点M在平面π上的充要条件 是MoM,n垂直.即MoM·n=0 (2)又MM=(x-xy-o,2-2o) 故点M在平面π上的充要条件是 我们把与平面垂直的非零向量 A(x-x)+By-)+C(z-20)=0 叫做平面的法线向量. 平面的点法式
在空间给定了一点M0 和一个非零 二、平面的点法式方程 x y z o M0 M n 量 n ,那么通过M0 且与 向量n垂直的平面也惟一地被确定. 我们把与平面垂直的非零向量 叫做平面的法线向量. 求过定点 ( , , ) 0 0 0 0 M x y z 且法向量为 n A B C , , 平面 方程 (1)设点 M x y z ( , , )是平面 上任意的一点 则点 M 在平面 上的充要条件 是 0 M M n, 垂直. 即 0 M M n 0 (2)又 M M x x y y z z 0 0 0 0 , , 故点 M 在平面 上的充要条件是 0 0 0 A x x B y y C z z ( ) ( ) ( ) 0 平面的点法式

二、平面的点法式方程 注记2:利用点法式求平面方程的步骤 例1求过M(2,-1,4),M(-1,3,-2) (1) 找出平面上的一个点M(xo,yo,2o) 和M3=(0,2,3)的平面的方程 解 (1)显然MM,=(-3,4,-6) (2) 找出平面上的法向量方=(A,B,C) M,M?=(-2,3,-1) (3) 代入点法式方程中,并整理化简 (2) 取法向量n=MM,×MM则 分析(1)取平面上的一个点M,(2,-1,4) n=-34 -6 =14i+9j-k (2)法向量n⊥M1M2,n⊥MM3, -23-1 因此 i‖MM×M,M 故平面的点法式方程为 故取 14(x-2)+9y+1)-(z-4)=0 n=M,M2×M,M 即 14x+9y-z-15=0
二、平面的点法式方程 注记 2:利用点法式求平面方程的步骤 (1) 找出平面上的一个点 ( , , ) 0 0 0 0 M x y z (2) 找出平面上的法向量n A B C , , (3) 代入点法式方程中,并整理化简 例 1 求过 1 2 M M (2, 1,4), ( 1,3, 2) 和 3 M (0,2,3)的平面的方程. 分析(1)取平面上的一个点 1 M (2, 1,4) (2)法向量 1 2 1 3 n M M n M M , , 因此 n M M1 2 M M1 3 故取 n M M1 2 M M1 3 解 (1)显然 1 2 M M ( 3,4, 6) 1 3 M M ( 2,3, 1) 3 4 6 2 3 1 i j k n (2)取法向量 1 2 1 3 n M M M M 则 14 9 i j k 故平面的点法式方程为 14( 2) 9( 1) ( 4) 0 x y z 即 14 9 15 0. x y z

三、平面的一般式方程 结论:空间中任一平面的方程都可表示成一个关于变量x,y,z的一次方程; 反过来,每一个关于变量x,y,z的一次方程都表示一张平面, Ax+By+Cz+D=0 平面的一般式 (A,B,C不同时为零) 注记3:空间中平面的一般式方程是平面中直线一般式方程的推广 注记4:平面一般方程的系数A,B,C是平面法向量的坐标 注记5:与Ax+By+Cz+D=0平行的平面的方程可以表示为 Ax+By+Cz+=0 注记6:利用一般式求平面方程时,只要求出A,B,C,D四个数的比值
机动 目录 上页 下页 返回 结束 三、平面的一般式方程 结论:空间中任一平面的方程都可表示成一个关于变量 x y z , , 的一次方程; 反过来,每一个关于变量 x y z , , 的一次方程都表示一张平面. 0 ( , , Ax By Cz D A B C 不同时为零) 平面的一般式 注记3:空间中平面的一般式方程是平面中直线一般式方程的推广 注记 4:平面一般方程的系数 A,B,C 是平面法向量的坐标. 注记 5:与 Ax By Cz D 0平行的平面的方程可以表示为 Ax By Cz 0 注记 6:利用一般式求平面方程时,只要求出 A B C D , , , 四个数的比值
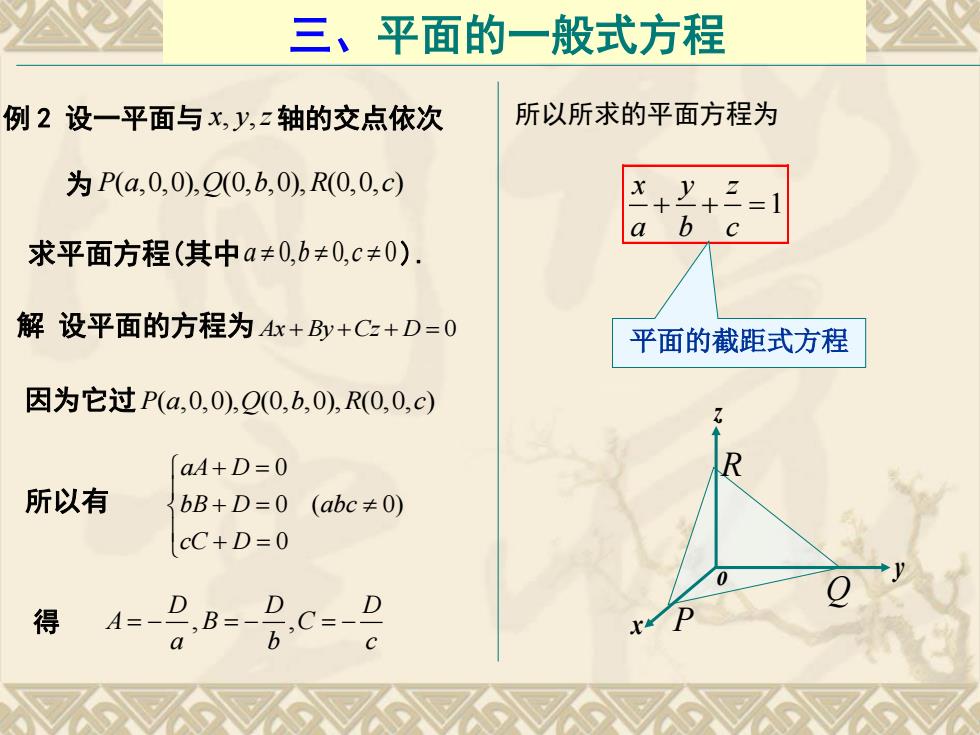
三、平面的一般式方程 例2设一平面与x,y,z轴的交点依次 所以所求的平面方程为 为P(a,0,0),Q(0,b,0),R(0,0,c) X +y+= a 求平面方程(其中a≠0,b≠0,c≠0) 解设平面的方程为Ax+By+Cz+D=0 平面的截距式方程 因为它过P(a,0,0),Q0,b,0),R0,0,c) aA+D=0 所以有 bB+D=0 (abc≠0) cC+D=0 得 48=8c=8
三、平面的一般式方程 例 2 设一平面与 x y z , , 轴的交点依次 为 P a Q b R c ( ,0,0), (0, ,0), (0,0, ) 求平面方程(其中abc 0, 0, 0 ). 解 设平面的方程为 Ax By Cz D 0 因为它过P a Q b R c ( ,0,0), (0, ,0), (0,0, ) 所以有 0 0 ( 0) 0 aA D bB D abc cC D 得 , , D D D A B C a b c 所以所求的平面方程为 1 x y z a b c 平面的截距式方程 x y z o P Q R

三、平面的一般式方程 平面过原点的充要条件是D=0 平面不过原点的充要条件是D≠0 平面过x轴的充要条件是A=D=0 平面平行于x轴的充要条件是A=0,D≠0 平面过y轴的充要条件是B=D=0 平面平行于y轴的充要条件是B=0,D≠0 平面过z轴的充要条件是C=D=0 平面平行于z轴的充要条件是C=0,D≠0 平面平行于xoy面的充要条件是 平面平行于0y面的充要条件是 A=B=0,D≠0 B=C=O,D≠0 平面平行于xoz面的充要条件是 例3求通过点x轴和点(4,-3,-)的平面的方 A=C=0,D≠0 解设过x轴的平面的方程为y+Cz=0.因为它过(4,-3,-1),所以有 -3B-C=0, 解得C=-3B,从而B:C=-1:3所以所求的平面方程为y-3z=0
三、平面的一般式方程 平面过原点的充要条件是D 0 平面不过原点的充要条件是D 0 平面过 x 轴的充要条件是 A D 0 平面平行于 x 轴的充要条件是 A D 0, 0 平面过 y 轴的充要条件是B D 0 平面平行于 y 轴的充要条件是B D 0, 0 平面过 z 轴的充要条件是C D 0 平面平行于 z 轴的充要条件是C D 0, 0 平面平行于 xoy面的充要条件是 A B D 0, 0 平面平行于 zoy 面的充要条件是 B C D 0, 0 平面平行于 xoz 面的充要条件是 A C D 0, 0 例 3 求通过点 x轴和点(4, 3, 1) 的平面的方程. 解 设过 x轴的平面的方程为By Cz 0 .因为它过(4, 3, 1) ,所以有 3 0, B C 解得 C B 3 ,,从而 B C: 1:3 所以所求的平面方程为 y z 3 0

四、两平面的夹角及特殊位置的判定 1:1 两平面的夹角: 即cos0= 44+BB+CC2 平面Π,几,的法线向量元,,的夹角 42+B2+C2++C2 (通常指锐角)称为两平面的夹角, 例4求出两平面2x-y+z-6=0 若记0是几,几,的夹角,则 x+y+2z-5=0的夹角 cos0=cos∠(i,i,) 解 显然两平面的法向量 m=(2,-1,1),m2=(1,1,2) 2×1+(-1)×1+1×2 cos0=- 22+(-102+1PP+P+22 2 因此
四、两平面的夹角及特殊位置的判定 1:两平面的夹角: 平面 1 2 , 的法线向量 1 2 n ,n 的夹角 (通常指锐角)称为两平面的夹角. 若记 是 1 2 , 的夹角,则 1 2 cos cos ( , ) n n 1 2 1 n 2 n 即 cos = 1 2 1 2 1 2 2 2 2 2 2 2 1 1 1 2 2 2 A A B B C C A B C A B C 例 4 求出两平面2 6 0 x y z x y z 2 5 0的夹角. 解 显然两平面的法向量 n n 1 2 2, 1,1 , 1,1,2 cos = 2 2 2 2 2 2 2 1 ( 1) 1 1 2 1 2 ( 1) 1 1 1 2 2 因此 3

四、两平面的夹角及特殊位置的判定 2 两平面特殊位置关系的判定 注记P(x,%,o)到平面A+By+Cz+D=0 (1)平面Π,与几,垂直的充要条件是 距离为 44,+B,B2+CC2=0 d=4%o+Byo+Czo+D 2+B2+C2 (2)平面Π,与Π,平行的充要条件是 考研题(96,3分)设一平面经过点(6,-3,2) 4-B-G≠D A B,C2 D. 且与平面2x+4y-2=0平行 (3)平面与几,重合的充要条件是, 则此平面方程为 4=B=9=D A,B,C,D
四、两平面的夹角及特殊位置的判定 2 两平面特殊位置关系的判定 (1)平面1 与2 垂直的充要条件是 . A1 A2 B1 B2 C1 C2 0 . (2)平面1 与2 平行的充要条件是. 1 1 1 1 2 2 2 2 A B C D A B C D . (3)平面1 与2 重合的充要条件是. 1 1 1 1 2 2 2 2 A B C D A B C D . 注记 0 0 0 0 P x y z ( , , )到平面 Ax By Cz D 0 距离为 0 0 0 2 2 2 | | Ax By Cz D d A B C 考研题(96,3 分)设一平面经过点(6, 3,2) 且与平面2 4 0 x y z 平行 则此平面方程为__________