§6.2可分离变量的微分方程 主要 内 容 阶可分离 阶可分离 变量的微 变量的微 分方程概念 分方程的求法
§6.2 可分离变量的微分方程 一阶可分离 变量的微 分方程概念 主 要 内 容 一阶可分离 变量的微 分方程的求法

阶可分离变量的微分方程的定义 观察 (1)y'=2xy ((2) x灯y'=yln 发现 (1) Idy=2xdx (2) dy =-dx yIny 共性具有8(y)y=f(x)dk形式 定义:如果一个一阶微分方程能写成g(y)=f(x)k的形式即 (1)一端只含y的函数和dy 如何求 一阶可分离变量微分方程的解? (2)另一端只含x的函数和dx 那么原方程就称为可分离变量的微分方程
一、一阶可分离变量的微分方程的定义 观察 (1) y xy 2 (2) xy y y ln 发现 (1) 1 dy xdx 2 y (2) 1 1 ln dy dx y y x 共性具有 g y dy f x dx ( ) ( ) 形式 定义:如果一个一阶微分方程能写成 g y dy f x dx ( ) ( ) 的形式即 (1)一端只含 y 的函数和dy (2)另一端只含 x 的函数和dx 那么原方程就称为可分离变量的微分方程 如何求 一阶可分离变量微分方程的解?
二、一阶可分离变量的微分方程求法 阶微分方程g(y)d=f(x)d 设g(y),fx)的原函数分别为G(y),F(x) 两边积分 不定积分定义 「g(y)dy=「f(x)d g(y)dy=G(y)+C ∫fx)dk=Fx)+C2 g=Fx+ 由方程Gy)=F(x)+C所确定的隐函数就是原方程的通解
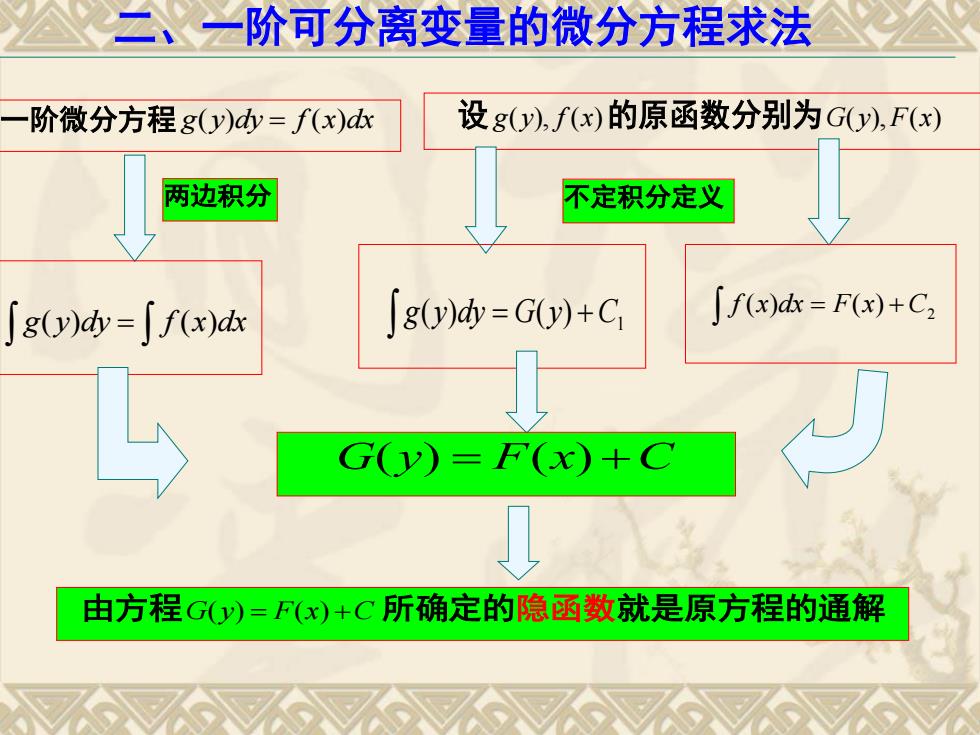
一阶微分方程 g y dy f x dx ( ) ( ) 设g y f x ( ), ( )的原函数分别为G y F x ( ), ( ) 两边积分 g y dy f x dx ( ) ( ) 1 g(y)dy G(y) C 2 f (x)dx F(x) C 不定积分定义 G y F x C ( ) ( ) 由方程G y F x C ( ) ( ) 所确定的隐函数就是原方程的通解 二、一阶可分离变量的微分方程求法

二、一阶可分离变量的微分方程求法 求一阶可分离变量微分方程通解步骤 例1求微分方程安=2的通解。 第一步 分离变量,将方程写成 解: 分离变量,将方程写成 g(y)dy=f(x)dx -=2xd 2 第二步 两端积分:∫g0)=∫fx) 两端积分: 得到 G(y)=F(x)+C 得到 Iny=x2+C 第三步求出由G(y)=F(x)+C所确定的 即 隐函数y=o(w)(或x=wy)就是通解 记 C=±e9,则方程的通解为y=Ce 微分方程的通解 dy d =2y的通解y=Ce 不一定 是所有的解 丢失了y=0
求一阶可分离变量微分方程通解步骤 第一步 分离变量 将方程写成 g y dy f x dx ( ) ( ) 第二步 两端积分 g(y)dy f (x)dx 得到 G y F x C ( ) ( ) 第三步 求出由G y F x C ( ) ( ) 所确定的 隐函数 y x ( ) (或 x y ( ) ) 就是通解 例 1 求微分方程 xy dx dy 2 的通解 解: 分离变量 将方程写成 xdx y dy 2 两端积分 xdx y dy 2 得到 1 2 ln y x C 即 2 1 C x y e e 记 C1 C e ,则方程的通解为 2 x y Ce 微分方程的通解 不一定 是所有的解 xy dx dy 2 的通解 2 x yCe 丢失了 y 0 二、一阶可分离变量的微分方程求法

二、一阶可分离变量的微分方程求法 通过变换可否化为 dy I 例2:求方程 一阶可分离变量微分方程 x+y 解:设x+y=w,则y=u-x d1= _-1.于是 即 du u+l dxdx dx u 分离变量得 u du=dx u+1 两边积分得 u-Inu+1=x+C 将u=x+y代入可得y-lnx+y+1=C 即 x=Ce"-y-1
例 2:求方程 dy 1 dx x y 解:设 xyu ,则 , 1 dy du y u x dx dx . 于是 1 1 du dx u 即 du u 1 dx u 分离变量得 1 u du dx u 将 u x y 代入可得 1 y x y C ln 1 即 1 y x Ce y 两边积分得 1 u u x C ln 1 通过变换可否化为 一阶可分离变量微分方程 二、一阶可分离变量的微分方程求法