第三节二元函数的全微分 全微分的 定义 可微与 主要 可微的 连续关系 内容 条件 全微分 应用
全微分的 定义 可微与 连续关系 可微的 条件 全微分 应用 主 要 内 容 第三节 二元函数的全微分

全微分的定义 类比推广 联想:如果函数y=fx)在点x的增量 定义:如果函数:=fx,y)在点(x,)的全增量 △y=f(x+△x)-f(x) △=fx+△x,y+Ay)-fx,y) 可表示为 可表示为 △y=A△x+o(△x) △=A△x+B△y+O(P) (1)A不依赖于△x而仅与x有关, (1)AB不依赖于△x,△y而仅与x,y有关 (2)o(△x)是比△x高阶的无穷小量 2) o(p)是比p=√△+(△高阶无穷小 则称函数y=)在点x可微 量,则称函数:=fx,)在点(x,)可微 称AAx为函数y=fm在点x的微分 称A△r+BAy为z=fx,y)在点(x,)的微分 记作y即 dy=A△x 记作dz即 d止=A△x+B△
一、 全微分的定义 联想: 如果函数 y f x ( )在点x的增量 y f x x f x ( ) ( ) y A x o x ( ) 可表示为 (1) A不依赖于x 而仅与 x 有关 (2) o x ( ) 是比x 高阶的无穷小量 则称函数 y f x ( )在点x可微 称A x 为函数y f x ( )在点x的微分 记作dy 即 dy A x 定义: 如果函数z f x y ( , )在点( , ) x y 的全增量 z f x x y y f x y ( , ) ( , ) z A x B y o( ) 可表示为 (1) A B, 不依赖于 x y , 而仅与x y, 有关 (2) o( ) 是比 2 2 ( ) ( ) x y 高阶无穷小 量,则称函数z f x y ( , )在点( , ) x y 可微 称 A x B y 为z f x y ( , )在点( , ) x y 的微分 记作dz 即 dz A x B y 类比推广
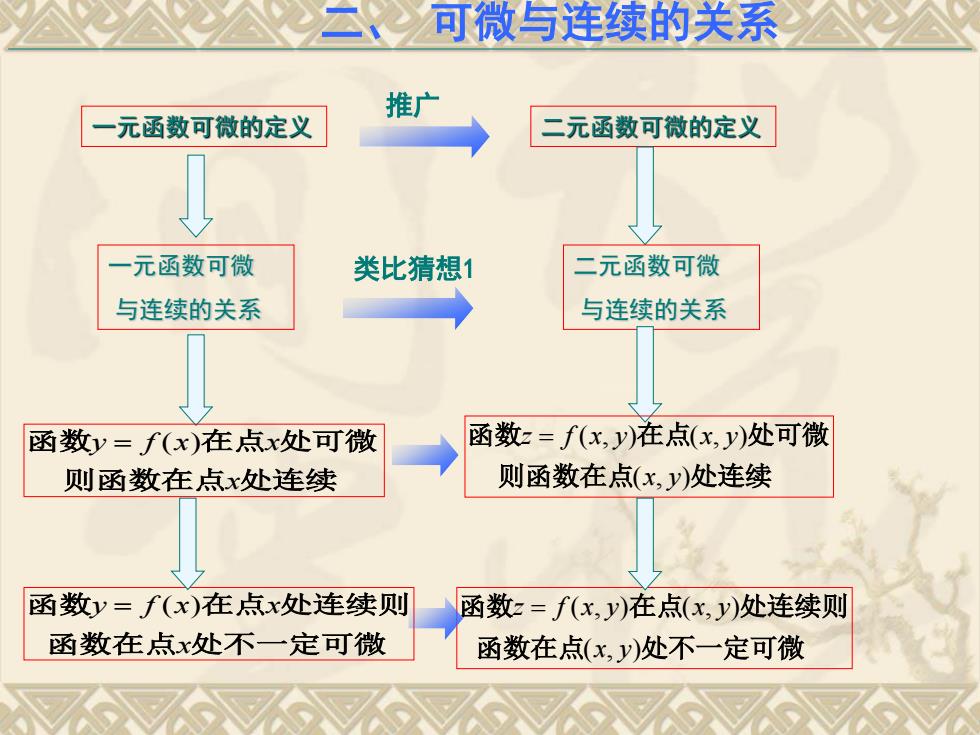
可微与连续的关系 推广 一元函数可微的定义 二元函数可微的定义 元函数可微 类比猜想1 二元函数可微 与连续的关系 与连续的关系 函数y=f(x)在点x处可微 函数z=f(x,y)在点(x,y)处可微 则函数在点x处连续 则函数在点(x,y)处连续 函数y=f(x)在点x处连续则 函数z=f(x,y)在点(x,y)处连续则 函数在点x处不一定可微 函数在点(x,y)处不一定可微
推广 一元函数可微的定义 二元函数可微的定义 一元函数可微 与连续的关系 二元函数可微 与连续的关系 类比猜想1 ( , ) ( , ) ( , ) z f x y x y x y 函数 在点 处可微 则函数在点 处连续 y f x x ( ) x 函数 在点 处可微 则函数在点 处连续 y f x x ( ) x 函数 在点 处连续则 函数在点 处不一定可微 ( , ) ( , ) ( , ) z f x y x y x y 函数 在点 处连续则 函数在点 处不一定可微 二、 可微与连续的关系

探究猜想1的正确性会之△心 函数:=x,)在点x,)处可微 函数:=fx,)在点x,)处连续 微分 连铁 定义 定义 △=A△x+B△y+o(p) lim。f(x+△x,y+△y)=f(x,y (Ax,△y)→(0,0) 当(△x,△)→0.0)时 △x→0,△y→0,p→0 lim.△z=limA△x+limB△y+limo(p)=O (△x,△y)(0,0) △x0 △y-0 p→0 极限的定义及运算法则 高阶无穷小的定义
z A x B y o( ) ? 微分 定义 当( , 0 0) x y) ( , 时 x 0, y 0, 0 ( , ) (0,0) 0 0 0 lim lim lim lim ( ) 0 x y x y z A x B y o ( , ) (0,0) lim ( , ) ( , ) x y f x x y y f x y 探究猜想 1 的正确性 函数z f x y ( , )在点( , ) x y 处可微 函数z f x y ( , )在点( , ) x y 处连续 极限的定义及运算法则 高阶无穷小的定义 连续 定义

可微与连续的关系 定理1若函数:=fx,)在点(x,y)处可微,则 函数:=fx,)在点(x,)处连续 注记1如果函数:=fx,y)在点(x,)处不连续,则函数在点(x,y) 一定不可微, 注记2如果函数=fx,)在点(x,)处连续,则函数在点(x,) 不一定可微 连续是二元函数可微的 必要条件而非充分条件 思考题:举例说明
定理 1 若函数z f x y ( , )在点( , ) x y 处可微,则 函数z f x y ( , )在点( , ) x y 处连续 注记 1 如果函数z f x y ( , )在点( , ) x y 处不连续,则函数在点( , ) x y 一定不可微. 注记 2 如果函数z f x y ( , )在点( , ) x y 处连续,则函数在点( , ) x y 不一定可微. 连续是二元函数可微的 必要条件而非充分条件 思考题:举例说明 二、 可微与连续的关系

、二元函数可微分的条件 类比推广 联想:一元函数y=f)在点X可微 猜想:如果函数:=fx,)在点(x,y)可微 的必要条件 的必要条件 如果函数y=fx)在点x可微 如果函数:=fx,y)在点(x,y)可微 则(1) 导数少必定存在 则(1)偏导数空、三必定存在 d (2) A=少=fx) (2) A=0 B& dx 可y 即函数y=f)在点x的微分为 即函数:=fx,)在点(x,)全微分为 d=f'(x)△x de=Ax+ 若记△x=,则 若记△x=dk,△y=dy,则 dy f'(x)dx y 止=产k+9 Ox y
三、二元函数可微分的条件 联想:一元函数 y f x ( )在点 x 可微 的必要条件 猜想: 如果函数z f x y ( , )在点( , ) x y 可微 的必要条件 类比推广 如果函数 y f x ( )在点 x 可微 则(1) 导数 dy dx 必定存在 (2) ( ) dy A f x dx 即函数 y f x ( )在点x的微分为 dy f x x ( ) 若记 x dx,则 dy f x dx ( ) 如果函数z f x y ( , )在点( , ) x y 可微 则(1)偏导数 x z 、 y z 必定存在 (2) , z z A B x y 即函数z f x y ( , )在点( , ) x y 全微分为 z z dz x y x y 若记 x dx y dy , ,则 z z dz dx dy x y
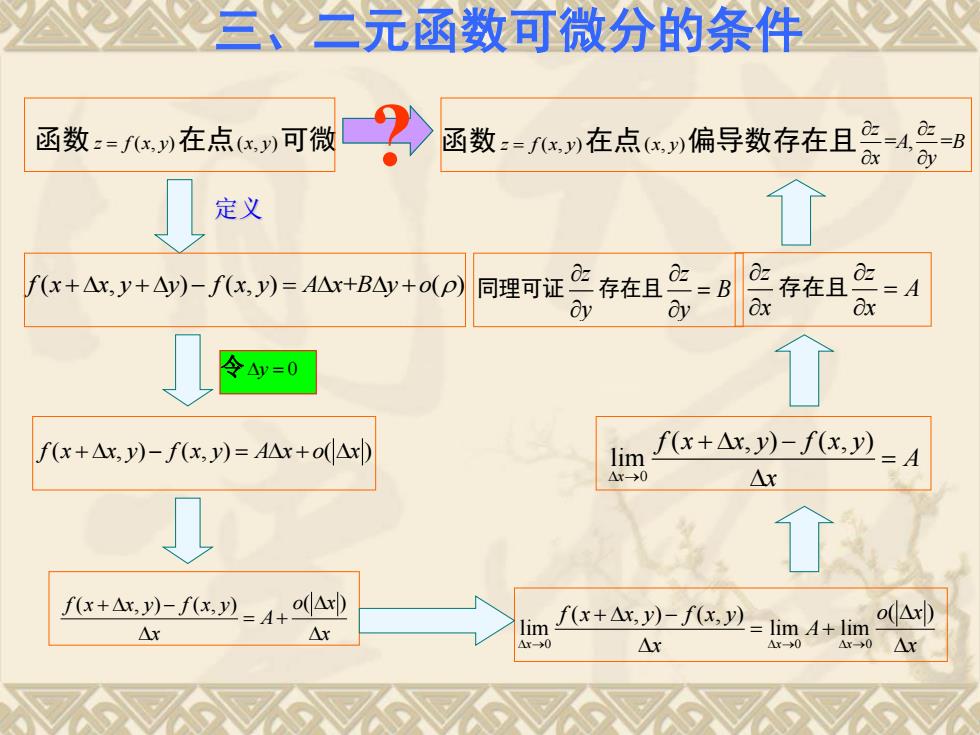
、二元函数可微分的条件 函数:=fx)在点x,)可微 函数:=fx,)在点x,)偏导数存在且产=4 z=B 定义 f(x+△x,y+△y)-f(x,y)=A△+B△y+o(P) 同理可证空存在且空=B 存在且应=A &x 令y=0 fx+△x,y)-f(x,y)=A△x+o(△x lim f(x+△x,y)-f(x,y) :A △x-→0 △x fx+A,月-fy=4+ f(x+△x,y)-f(x,y )lim 4+lim o(△x) △x Ar lim △x
函数z f x y ( , )在点( , ) x y 可微 ? 定义 函数z f x y ( , )在点( , ) x y 偏导数存在且 = , = z z A B x y f x x y y f x y A x B y o ( , ) ( , ) + ( ) f x x y f x y A x o x ( , ) ( , ) ( ) f x x y f x y ( , ) ( , ) o x ( ) A x x 0 0 0 ( , ) ( , ) ( ) lim lim lim x x x f x x y f x y o x A x x 0 ( , ) ( , ) lim x f x x y f x y A x 同理可证 z y 存在且 z B y 令 y 0 z x 存在且 z A x 三、二元函数可微分的条件
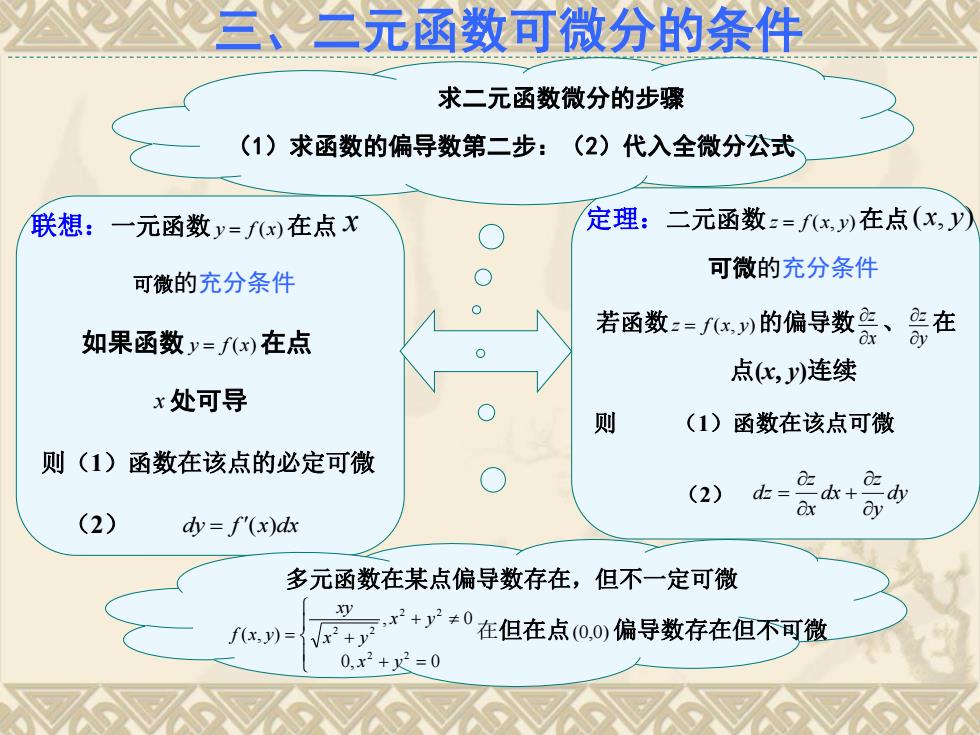
、二元函数可微分的条件 求二元函数微分的步骤 (1)求函数的偏导数第二步:(2)代入全微分公式 联想:一元函数y=fw)在点X 定理:二元函数:=fx,)在点(x,) 可微的充分条件 可微的充分条件 如果函数y=f(x)在点 若函数:=x列的偏导数票、等在 点化,y)连续 x处可导 则 (1)函数在该点可微 则(1)函数在该点的必定可微 (2) d= 0 -dx+ dy (2) dy dy f"(x)dx 多元函数在某点偏导数存在,但不一定可微 y f(x,y)= +)r+”+0在但在点0,0偏导数存在但不可微 0,x2+x2=0
三、二元函数可微分的条件 联想:一元函数 y f x ( )在点 x 可微的充分条件 如果函数 y f x ( )在点 定理:二元函数z f x y ( , )在点( , ) x y 可微的充分条件 若函数z f x y ( , )的偏导数 x z 、 y z 在 点(x y)连续 则 (1)函数在该点可微 (2) dy y z dx x z dz 则(1)函数在该点的必定可微 (2) dy f x dx ( ) x 处可导 多元函数在某点偏导数存在,但不一定可微 0, 0 , 0 ( , ) 2 2 2 2 2 2 x y x y x y xy f x y 在但在点(0,0)偏导数存在但不可微 求二元函数微分的步骤 (1)求函数的偏导数第二步:(2)代入全微分公式

四、二元函数的近似计算 由二元函数全微分的定义及 用全微分求函数近似值的步骤 存在的充分条件可知 第一步:设出函数2=f(x,y)确定 (1)当二元函数z=f(x,y)在点(x,y) xo,y0,△x,△y 的偏导数气连续 (△A较小f(x,)容易计算) (2)并且△xAy都较小时 第二步:求出(xf'(x,%)及 有近似等式. f(x,) △正≈d=∫(x,y)△x+∫(x,y)Ay 第三步:代入公式求出f:+△x,,+△) f(x+△x,y+Ay)≈f(x,y)+ 近似值 f'(x,y)△x+f,(xy)△y
四、二元函数的近似计算 由二元函数全微分的定义及 存在的充分条件可知 (1)当二元函数 z f (x, y)在点( , ) x y 的偏导数 y z x z , 连续 (2)并且 x , y 都较小时 有近似等式. z dz f x y x f x y y x ( , ) y ( , ) ( , ) ( , ) ( , ) ( , ) x y f x x y y f x y f x y x f x y y 用全微分求函数近似值的步骤 第一步:设出函数 z f (x, y) 确定 0 0 x y x y , , , ( x , y 较小 0 0 f x y ( , ) 容易计算) 第二步:求出 0 0 0 0 ( , ), ( , ) x y f x y f x y 及 0 0 f x y ( , ) 第三步:代入公式求出 0 0 f x x y y ( , ) 近似值

例题 例1计算函数:=x2y+y2的全微分 (2)故 dx+ dy 解(1)因为票-2w =e'dx +2e'dy =x2+2y ay 例3计算1.04)22的近似值 (2)止=2k+山 解设函数f(x,y)=x,取x=1,%=2, △x=0.04,△y=0.02 =23yk+(x2+2y)dy 由于(x,)=x,f'(x,)=xnx,所以 例2求z=e在点(2,1)的全微分. f1,2)=2,f1,2)=0,fL,2)=1 解(1)因为 =ye”, (1.04)202=f(x+△x,6+△y) ≈f(x,6)+'(x,6)△x+,'(x)Ay 所以 =e2 -2e2 ≈1+2×0.04+0×0.02≈1.08
例 题 例 1 计算函数 2 2 z x y y 的全微分 例 2 求 xy z e 在点(2,1)的全微分. (2) 解 (1) 因为 xy x z 2 z z dz dx dy x y x y y z 2 2 2 2 ( 2 ) xydx x y dy 解 (1) 因为 , z xy ye x xy xe y z 所以 2 (2,1) , z e x 2 (2,1) 2 z e y (2) 故 (2,1) (2,1) (2,1) z z dz dx dy x y 2 2 e dx e dy 2 例 3 计算 2.02 (1.04) 的近似值 解 设函数 ( , ) y f x y x ,取 0 0 x y 1, 2, x y 0.04, 0.02 由于 1 ( , ) , ( , ) ln y y x y f x y yx f x y x x ,所以 (1,2) 2, (1,2) 0, x y f f f (1,2) 1 2.02 0 0 (1.04) ( , ) f x x y y 0 0 0 0 0 0 ( , ) ( , ) ( , ) x y f x y f x y x f x y y 1 2 0.04 0 0.02 1.08