南阳师范学院：《高等数学》课程教学资源（课件讲稿）第七章 向量代数与空间解析几何 §7.3 数量积、向量积、混合积

§7.3数量积、向量积、混合积 数量积 向量积 主要内容 平行垂直 混合积 的条件 坐标表示

§7.3 数量积、向量积、混合积 坐标表示 主要内容 混合积 数量积 向量积 平行垂直 的条件

两向量的数量积 定义：两向量a与的模和它们 性质(1)aa=d=a2 夹角的余弦的乘积叫做 (2)当a=0或b=0时 两向量a和的数量积.记做 a.b=0 a.6或ab 当ā≠0，五≠0时 a.b=lacos.∠(a,) a.b=dPrjb=bPrjga i.i=j.j=k.k=1 (3)a.b=0⊙a1b i.j=i.k=j.k=0

一、 两向量的数量积 定义：两向量 a 与 b 的模和它们 夹角的余弦的乘积叫做 两向量a 和b 的数量积. 记做 a b    或 ab   a b a b a b    cos ( , ) 性质（1） 2 2 a a a a    i i j j k k      1 （3） a b a b       0   i j i k j k       0 （2）当 a  0或b  0时 当 a b   0, 0 时 a b a j b b j a a b        Pr   Pr   a b  0

一 两向量的数量积 b-a=acos-∠(6，d←☐定义→a:6=la6lcos∠(a,b) ∠(a,b)=∠(b,a) a.b=b.a (a+b)c=0 (a+b)-c=cPrjg(a+b) ac=0,b.c=0 c=0 对于c c≠0 和的投影等 (a+b)c=0 (a+b).c=cPrja+cPrjb a.c+b.c=0 于投影之和 (a+b).c=a.c+b.c

一、 两向量的数量积 定义 a b a b a b    cos ,   b a b a b a    cos ,      a b b a , ,    a b b a        对于c c  0 c  0 ( ) 0 0, 0 a b c a c b c        (a b) c c Pr j (a b) c            a b c c j c a c j c b        (  )  Pr   Pr  ( ) 0 0 a b c a c b c        a b c a c b c        (  )     和的投影等 于投影之和

两向量的数量积 λa=0 6=0 6≠0 对于五 (Aa).B=B Prj;(Aa) 入(a.b)=0 A(a.B)=BPri;a 数乘向量的投 影等数乘 (a)b=0 (Aa).B=BPrjja 该向量的投影 (a.b)=0 A(a-B)=1BPrJa (a)-b=(a.b)

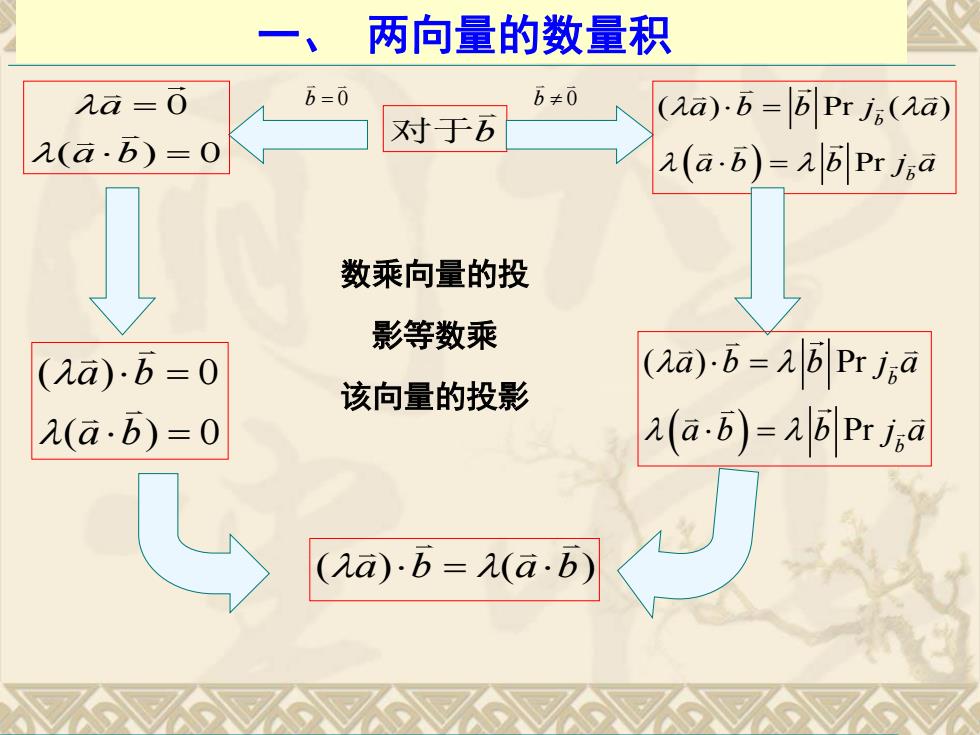
一、 两向量的数量积 对于b b  0 b  0 0 ( ) 0 a a b        ( ) Pr ( ) Pr b b a b b j a a b b j a           ( ) Pr Pr b b a b b j a a b b j a         ( ) 0 ( ) 0 a b a b       ( ) ( )   a b a b    数乘向量的投 影等数乘 该向量的投影

一、两向量的数量积 数量积运算规律与数量乘法运算规律的比较 (1)交换律a.b=b.a (1)交换律a·b=b·a (2) 关于数因子的结合律 (2) 结合律 (a)b=2(a.b)=a(2b) (2a)b=(ab)=a(b) (3)分配律 (3)分配律 (a+b).c=a.c+b.c (a+b)c=ac+b·C (4)(ab)c=a(bc)一般不成立 (4)(ab)c=a(be) (5)a记=bc,c≠0推不出a=b. (5)ac=bc,c≠0必有a=b

数量积运算规律与数量乘法运算规律的比较 一、两向量的数量积 （1）交换律 a b b a        （2） 关于数因子的结合律 ( a) b (a b) a ( b)               （3）分配律 a b c a c b c        (  )     （4） (ab)c a(bc)        一般不成立 （5）ac bc c   , 0 推不出a b  . （1）交换律 a b b a    （2） 结合律 ( ) ( ) ( )    a b a b a b      （3）分配律 ( ) a b c a c b c       （4） ( ) ( ) ab c a bc  （5）ac bc c   , 0必有a b 

一、两向量的数量积 数量积运算规律与数量乘法运算规律的比较 注记1做向量数量积运算时可以像 注记2利用数量积可以解决几何中 多项式的乘法那样运算 ()边的问题=v√a.d (1) (a+b)2=a2+2ab+b2 (2)角的问题 coS∠ABC=cos∠AB,AC) (2) (ā-b)2=a2-2ab+b2 AB.AC AB AC (3) (a+b(a-b)=a2-b2 (3)垂直的问题 AB⊥AC→AB.AC=0

数量积运算规律与数量乘法运算规律的比较 一、两向量的数量积 注记 1 做向量数量积运算时可以像 多项式的乘法那样运算 （1） 2 2 2 ( ) 2 a b a ab b     （2） 2 2 2 ( ) 2 a b a ab b     （3） 2 2 ( )( ) a b a b a b     注记 2 利用数量积可以解决几何中 （1）边的问题 a a a   （2）角的问题 cos cos ,    ABC AB AC   AB AC AB AC   （3）垂直的问题 AB AC AB AC     0

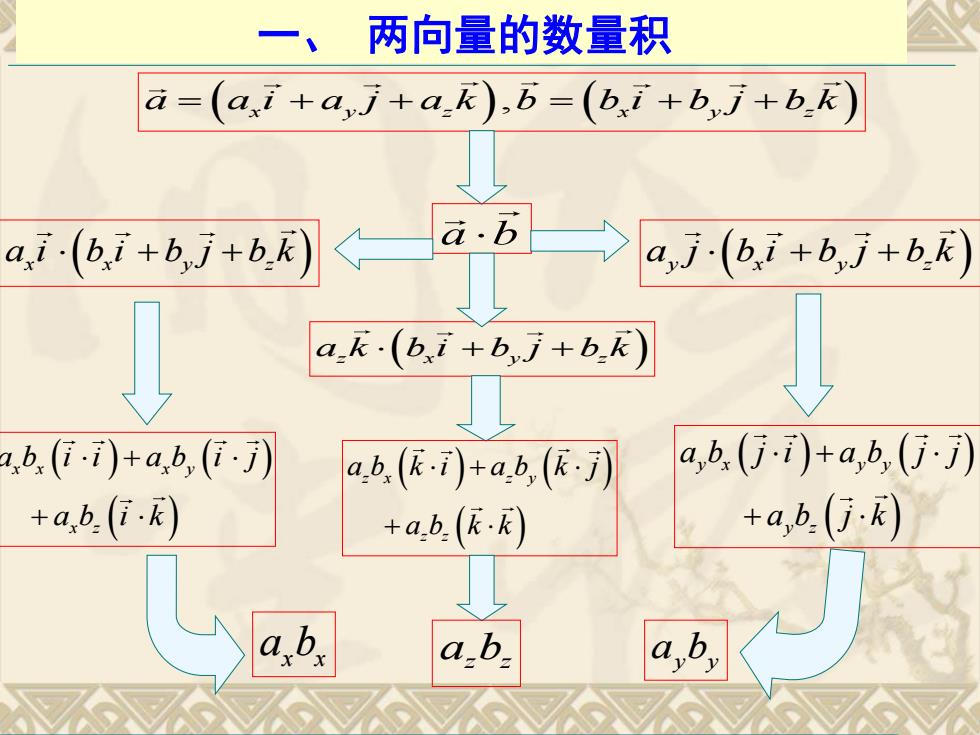
一、两向量的数量积 a=（ai+aj+aE),b=（bi+bj+bk) (67+么7+ba万→2j(6+6+6利 a_k.(bi+bj+bk) b,(ii)tab,(i.j) ab.(k.i）+ab,(j) a,b(ji)+a,b（jj) tab(i.k) +ab.(K.) +a,b.(j.R) ab. a.b

一、 两向量的数量积 a a i a j a k b b i b j b k        x y z x y z ,   a i b i b j b k x x y z      a b a j b i b j b k y x y z      a k b i b j b k z x y z            x x x y x z a b i i a b i j a b i k            y x y y y z a b j i a b j j a b j k            z x z y z z a b k i a b k j a b k k      x x a b a bz z a by y

一、两向量的数量积 数量积的坐标表示及向量的模及方向余弦 定理：若d=a,i+aj+ak MM=Vx-x)2+y-}+(2-)》2 B=bi+bj+bk 推论3：若非零向量ā=(x,y,z)与三条 则a.b=a,b,+a,b,+ab: 坐标轴的夹角为a,B,y,则 推论1：若a=ai+aj+a.R X cosa= 则 =Va,"+a,"ta. 称为的 同 x+y+ COS B= 推论2：若M,(,,),M,(,2,2) 方向余弦 A x+y+ 则MM,=(3-x,5-片，32-） x2+y2+2

一、两向量的数量积 数量积的坐标表示及向量的模及方向余弦 定理：若 x y z a a i a j a k    x y z b b i b j b k    则 x x y y z z a b a b a b a b     推论 1：若 x y z a a i a j a k    则 2 2 2 x y z a a a a    推论 2：若 1 1 1 1 2 2 2 2 M x y z M x y z ( , , ), ( , , ) 则 M M x x y y z z 1 2 2 1 2 1 2 1      , ,  2 2 2 1 2 2 1 2 1 2 1 M M x x y y z z       ( ) ( ) ( ) 推论 3：若非零向量a x y z  ( , , )与三条 坐标轴的夹角为   , , ，则 2 2 2 2 2 2 2 2 2 cos cos cos x x a x y z y y a x y z z z a x y z                           称为 r 的 方向余弦

两向量的数量积 例1已知点A(1,1,1),B(2,2,1), 求解题步骤 (1)求B的方向角 （1)求出4B坐标 AB=(1,1,0) (2)求与B的同方向的单位向量 (2)求出B的模AB=VP+1P+02=√V2 分析：（1)联想到4B的方向角满足 (3)求出AB的方向余弦 X cosa= Vx2+y2+2 cosa= y y .CosB=_ 1 2.cosy=0 Cos B= 同 2+y2+2 (4)求出B的方向角 cosy= √x2+y2+22 可得 a=(x,y,=)=a(cosa,cosB.cosy) (5)求出与4B的同方向的单位向量 (2)从而与与ā的同方向的单位向量 e=(cosa,cos B,cosy) e。=(cosa,cosB,cs）-2

一、 两向量的数量积 例 1 已知点 A B (1,1,1), (2,2,1), （1）求 AB 的方向角 （2）求与 AB 的同方向的单位向量 分析：（1）联想到 AB 的方向角满足 2 2 2 2 2 2 2 2 2 cos cos cos x x a x y z y y a x y z z z a x y z                           可得 a x y z a   ( , , ) (cos ,cos ,cos )    （2）从而与与a的同方向的单位向量 (cos ,cos ,cos ) a e     求解题步骤 （1）求出 AB 坐标 AB  1,1,0 （2）求出 AB 的模 2 2 2 AB     1 1 0 2 （3）求出 AB 的方向余弦 1 1 cos ,cos ,cos 0 2 2       （4）求出 AB 的方向角 , , 4 4 2          （5）求出与 AB 的同方向的单位向量   1 1 cos ,cos ,cos , ,0 2 2 a e           

两向量的数量积 例2：已知M(1,1,1),A(2,2,1),B(2,1,2) (3)计算MA,M,得到MA=MB （1)证明三点不共线 (4)计算cos(MA,M,得到∠AMB=60° (2)证明△4MB是底角为60°等腰三角形 证明：(1)显然MA=(1,1,0),MB=(1,0,1) 分析 由于1：1：0≠1：0：1，故MA,MB不共线 (1)联想三点M,A,B不共线的充要条件 是MA,MB不共线 因此M,A,B三点不共线 (2)联想到△4MB是底角为60°等腰 (2)由于M4=VP+P+0=2, 三角形的充要条件是两边相等底角 M=P+02+P=5 为60 cos∠AMB MA.MB 1×1+1×0+0×11 证明思路： MA MB √2×√2 （1)求出MAMB坐标 所以 ∠AMB=60° (2)判断MA,MB不共线从而M,A,B不共线 因此△4MB是底角为60°等腰三角形

一、 两向量的数量积 例 2：已知 M A B (1,1,1), (2,2,1), (2,1,2) （1）证明三点不共线 （2）证明AMB 是底角为 0 60 等腰三角形 分析 是 MA MB , 不共线 （2）联想到AMB 是底角为 0 60 等腰 三角形的充要条件是两边相等底角 为 0 60 （1）联想三点 M A B , , 不共线的充要条件 证明思路： （1）求出 MA MB , 坐标 （2）判断 MA MB , 不共线从而 M A B , , 不共线 （3）计算 MA MB , ，得到 MA MB  （4）计算 cos ,  MA MB ，得到 0   AMB 60 证明：（1）显然MA MB   1,1,0 , 1,0,1    由于1:1:0 1:0:1  ，故MA MB , 不共线 因此 M A B , , 三点不共线 （2）由于 2 2 2 MA     1 1 0 2 ， 2 2 2 MB     1 0 1 2 1 1 1 0 0 1 1 cos 2 2 2 MA MB AMB MA MB            ， 所以 0   AMB 60 因此AMB是底角为 0 60 等腰三角形