南阳师范学院：《高等数学》课程教学资源（课件讲稿）第九章 重积分及曲线积分 9.2 二重积分的计算

§9.2二重积分的计算 直角坐标系下二重 极坐标系下二重 积分的计算 积分的计算

§9.2 二重积分的计算 极坐标系下二重 积分的计算 直角坐标系下二重 积分的计算

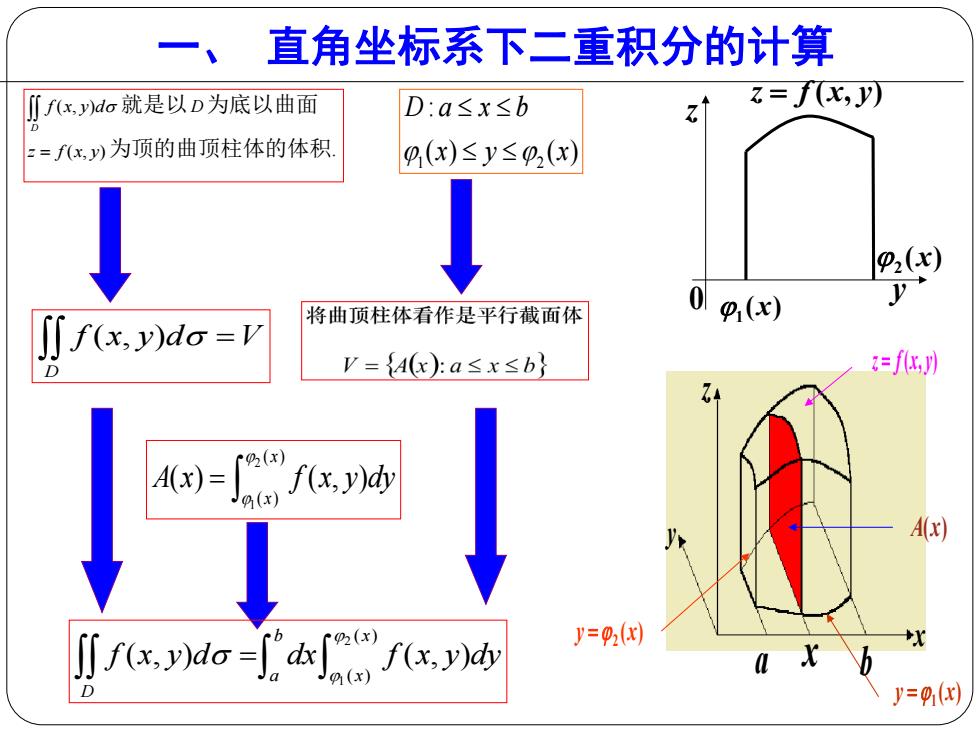
直角坐标系下二重积分的计算 I:o就是以D为底以曲面 D:a≤x≤b z=fx,J)】 z=fx,y)为顶的曲顶柱体的体积 0(x)≤y≤p(x) P2(x) f(x)do=严 将曲顶柱体看作是平行截面体 0p,(x) D D V={4x):a≤x≤b} f化，川 7 A(x) xnio-iaafxw =2田) 0 y=q1(）

一、 直角坐标系下二重积分的计算  D f (x, y)d 就是以D为底以曲面 z  f (x, y)为顶的曲顶柱体的体积. 1 2 : ( ) ( ) D a x b   x y x     ( , ) D f x y d V    0 y z z  f (x, y) ( ) 1  x ( ) 2  x z y x A(x) z  f (x, y) ( ) 1 y  x ( ) 2 y  x a x b 2 1 ( ) ( ) ( ) ( , ) x x A x f x y dy     2 1 ( ) ( ) ( , ) ( , ) b x a x D f x y d dx f x y dy       

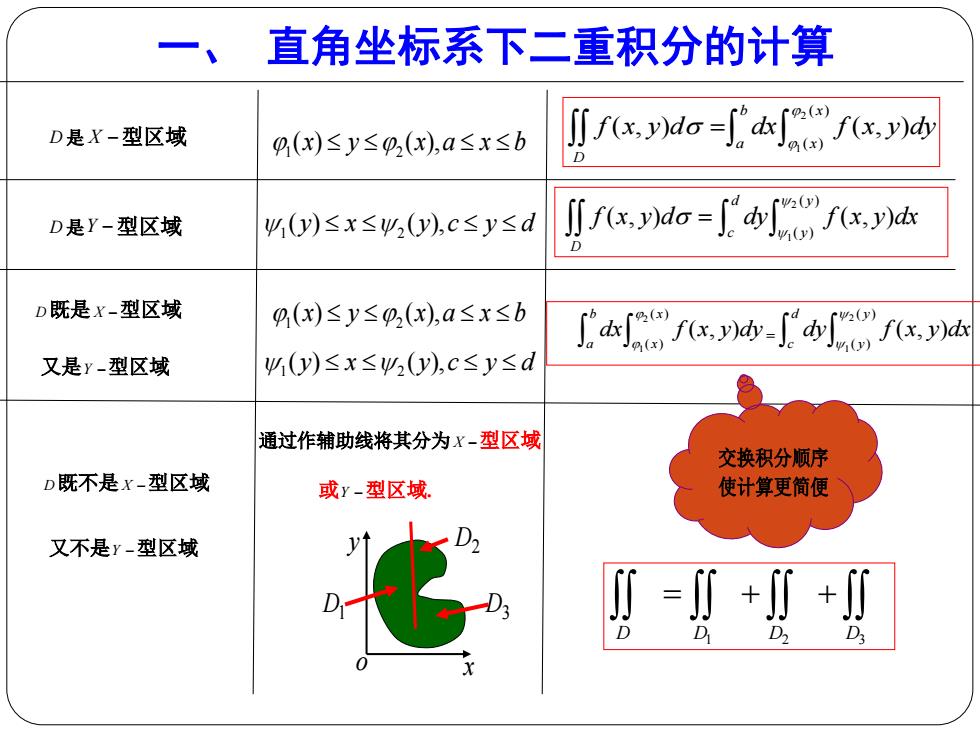
直角坐标系下二重积分的计算 D是X-型区域 0(x)≤y≤2(x,a≤x≤b fcxdo=ifcx,w D是Y-型区域 4y)≤x≤y2(y),c≤y≤d f,dia=ofx达 D既是x-型区域 0(x)≤y≤p,(x,a≤x≤b 广fx,w-fxa 又是y-型区域 4(y)≤x≤y),c≤y≤d 通过作辅助线将其分为X-型区域 交换积分顺序 D既不是x-型区域 或y-型区域 使计算更简便 又不是y-型区域 ∬=∬++川 D. D

D 是 X 型区域 1 2   ( ) ( ), x y x a x b     2 1 ( ) ( ) ( , ) ( , ) b x a x D f x y d dx f x y dy        D 是Y 型区域 1 2   ( ) ( ), y x y c y d     2 1 ( ) ( ) ( , ) ( , ) d y c y D f x y d dy f x y dx        D既是 X 型区域 又是Y 型区域 1 2   ( ) ( ), x y x a x b     1 2   ( ) ( ), y x y c y d     2 1 ( ) ( ) ( , ) b x a x dx f x y dy    = 2 1 ( ) ( ) ( , ) d y c y dy f x y dx    D既不是 X 型区域 又不是Y 型区域 通过作辅助线将其分为 X 型区域 或Y 型区域. o x y D1 D2 D3 D D D D 1 2 3        交换积分顺序 使计算更简便 一、 直角坐标系下二重积分的计算

直角坐标系下二重积分的计算 注记1：直角坐标下求二重积分的一般步骤 例1 计算∫(x+2y)do,其中D是由抛物线 第一步：画出闭区域的几何草图求出有 y=2x2,y=1+x2所围成的闭区域 解：画出闭区域D的几何图形.显然两抛 关的交点坐标 物线y=2x2,y=1+x2的交点为(L,2),(-1,2) 第二步：确定闭区域的类型，写出个区域的 因此D是X-区域： 不等式表达式 -1≤x≤1,2x2≤y≤1+x2 第三步：利用公式将二重化为二次积分 所以了 x+2do=∫2(x+2y)山 第四步：利用定积分的性质定理进行计算 =∫[y+y] （3r-42x+4a=君

一、 直角坐标系下二重积分的计算 注记 1： 直角坐标下求二重积分的一般步骤 第一步：画出闭区域的几何草图求出有 关的交点坐标 第二步：确定闭区域的类型，写出个区域的 不等式表达式 第三步：利用公式将二重化为二次积分 第四步：利用定积分的性质定理进行计算 例 1 计算 ( 2 ) D x y d    ，其中 D 是由抛物线 2 2 y x y x    2 , 1 所围成的闭区域 解：画出闭区域 D 的几何图形. 显然两抛 物 线 2 2 y x y x    2 , 1 的交点为(1,2),( 1,2)  因此 D 是 X  区域： 2 2       1 1, 2 1 x x y x 所以 ( 2 ) D x y d       2 2 1 1 1 2 2 x x dx x y dy        2 2 1 1 2 1 2 x x xy y dx             1 4 3 2 1 3 2 1 x x x x dx          32 15 

直角坐标系下二重积分的计算 例2计算∬do,其中p是直线y=1,x=2, 因此」 odo=广i y=x所围成的三角形闭区域 解：画出闭区域D的几何图形，显然直线 y=1,x=2,y=x的交点4(2,2)，B(2,1),C1,1) V (法2)显然积分区域是Y-区域： 1≤y≤2，y≤x≤2. B 01 心odo=小广 因此 (法1)显然积分区域是X-区域 1≤x≤2,1≤y≤x 8

一、 直角坐标系下二重积分的计算 例 2 计算 D xyd ，其中D是直线 y x   1, 2, y x  所围成的三角形闭区域 解：画出闭区域D的几何图形，显然直线 y x y x    1, 2, 的交点 A B C (2,2), (2,1), (1,1) x y O 1 1 2 A C B （法 1）显然积分区域是 X  区域 1 2,1 .     x y x 因此 2 1 1 x D xyd dx xydy       3 2 1 2 x x dx     9 8   （法 2）显然积分区域是Y  区域： 1 2, 2.     y y x 因此 2 2 1 y D xyd dy xydx       3 2 1 2 2 y y dy          9 8 

课堂训练1-判断正误 (1)设出闭区域D:0≤x≤1,0≤y≤1，则 f(x+3xy+yHo-Sdf(x'+3xy+y)do (2)设D由两坐标轴及直线x+y=2围成的闭区域，则 ∬3x+2o=0'(3x+20 (3)设D是顶点为0,0)，（π，0，（π，）的闭三角形，则 xco+y (4)设D是由直线y=2,y=x,y=2x围成的闭区域，则 +y+odo(+y+)d

课堂训练1-判断正误 （1）设出闭区域D：0 1,0 1     x y ，则     1 1 3 2 3 3 2 3 0 0 3 3 D x x y y d dx x x y y dy          （2）设 D由两坐标轴及直线x y   2围成的闭区域，则 2 2 0 0 (3 2 ) (3 2 ) x D x y d dx x y dy         （3）设 D是顶点为(0,0),( ,0),( , )    的闭三角形，则 0 0 cos( ) cos( ) y D x x y d dy x x y dx         （4）设 D是由直线 y y x y x    2, , 2 围成的闭区域，则     2 3 2 3 3 2 3 0 2 3 3 y y D x x y y d dy x x y y dx         

例3证明ifx=x+∫广源fx 分析(1)从左边看处区域D是Y-型 因此右边=∬fx,Ho+∬fx,o 区域：-1≤y≤2，y2≤x≤y+2 我们只需证明 因此 左边=∬fx,o X=y2 (2)右边第一部分dfx的积分 X= 区域D:-√≤y≤V,0≤x≤1是X-型区域 右边第二部分广fx,d的积分区域 [fc-[f(.c+(y D:x-2≤y≤V,1≤x≤4也是X-型区域 即 D=D+D

例 3 证明 2 2 2 1 ( , ) yy dy f x y dx      1 4 0 1 2 ( , ) ( , ) x x x x dx f x y dy dx f x y dy       x  12 x = y2 1 1 4 y 分 析（1）从左边看处区域 D 是 Y型 区域 2       1 2, 2 y y x y 因此 左边= ( , ) D f x y d   （2） 右边第一部分 10 ( , ) xx dx f x y dy   的积分 区域 1 D x y x x : ,0 1      是 X型区域 右边第二部分 4 1 2 ( , ) x x dx f x y dy    的积分区域 2 D x y x x : 2 ,1 4      也是 X型区域 因此 右 边= 1 2 ( , ) ( , ) D D f x y d f x y d      我们只需证明 1 2 ( , ) ( , ) ( , ) D D D f x y d f x y d f x y d         即 D D D  1 2

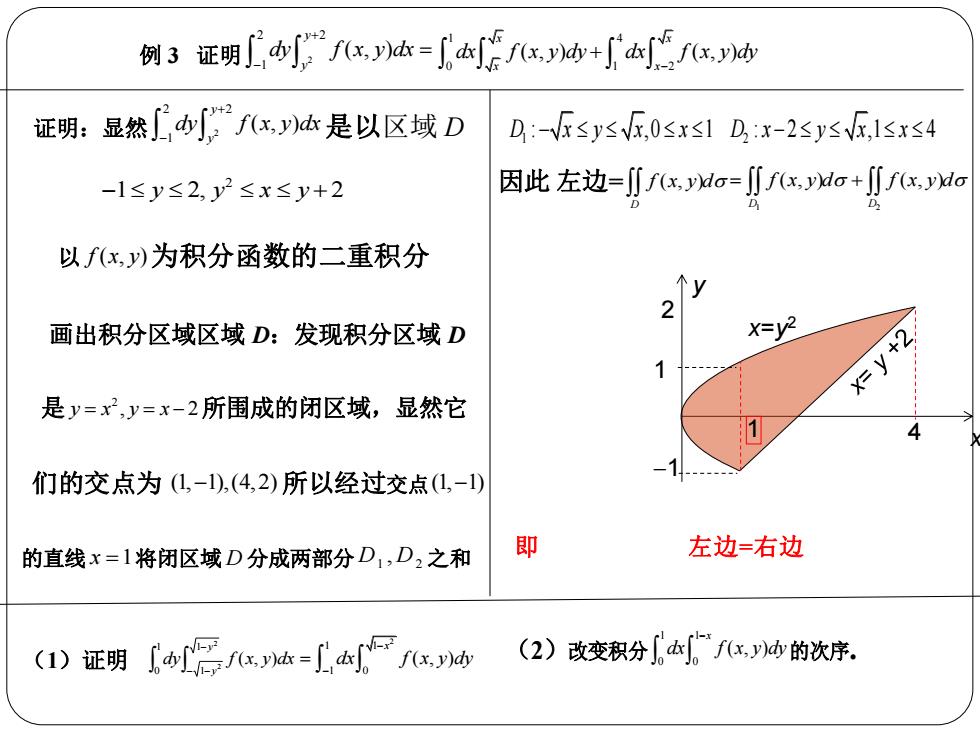
例3证明ifx,=fx+∫fx 证明：显然fxy)是以区域D D:-F≤ysG,0≤x≤1D,x-2sysG,1sx≤4 -1≤y≤2，y2≤x≤y+2 因此左边=o=fo+fo 以fx,)为积分函数的二重积分 2 画出积分区域区域D:发现积分区域D X=V2 2 x=y 是y=x2,y=x-2所围成的闭区域，显然它 们的交点为(1，-1)，(4,2)所以经过交点L,-1) 的直线x=1将闭区域D分成两部分D1,D2之和 即 左边=右边 (1)证明=Ff冰 (2)改变积分本fx,d的次序

例 3 证明 2 2 2 1 ( , ) yy dy f x y dx      1 4 0 1 2 ( , ) ( , ) x x x x dx f x y dy dx f x y dy       x  12 x = y2 1 1 4 y （1）证明      22 11 10 ( , ) yy dy f x y dx 2 1 1 1 0 ( , ) x dx f x y dy      （2）改变积分 1 1 0 0 ( , ) x dx f x y dy    的次序. 证明：显然 2 2 2 1 ( , ) yy dy f x y dx     是 以区域 D 2       1 2, 2 y y x y 以 f x y ( , )为积分函数的二重积分 画出积分区域区域 D：发现积分区域 D 是 2 y x y x    , 2 所围成的闭区域，显然它 们的交点为 (1, 1),(4,2)  所以经过交点(1, 1)  的直线 x  1将闭区域 D 分成两部分 1 2 D D, 之 和 1 2 D x y x x D x y x x : ,0 1 : 2 ,1 4           因此 左边= ( , ) D f x y d   1 2 ( , ) ( , ) D D   f x y d f x y d     即 左边=右边

例4计算 分析： D显然a布等于西数'在饲区罐因t广太一『四如 D:0≤x≤π，：x≤y≤π上二重积分 (2)如图所示为D的几何图形.显然D是由抛 -y 物线y=π及直线y-x,x=0所围成的闭区域 =f sin ydy=[cosy]=-2 (3)由于'小无法用初等函数表示出来 因此我们需要交换小的积分顺序 v=x y=π (4)显然D也是Y一型区域： 0≤y≤π，0≤x≤y π X

例 4 计 算 0 sin x y dx dy y     o x y D  y   y  x 分析： （1）显然 0 sin x y dx dy y     等 于函 数sin y y 在闭区域 D x x y :0 ,:       上二重积分 （2）如图所示为 D 的几何图形. 显然D 是由抛 物线 y   及直线 y x x   , 0所围成的闭区域 （3）由于 sin x y dy y   无法用初等函数表示出来 因此我们需要交换 0 0 x sin y dx dy y    的积分顺序. （4）显 然 D 也 是 Y型区域 0 , 0     y x y  0 sin x y dy dx y   因此   sin D y d y    0 0 y sin y dy dx y       0 0 sin cos 2 ydy y       

二、极坐标系下二重积分的计算 极坐标与直角坐标的关系 在极坐标系下，如何计算 x=pcoso 二重积分∬fx,ydo y=psino p=P+△0 0=9+△0 f(x,y)=f(pcoso,psin) do=pdpdp P=P △0 0=9 ∬fx,y)do=j∬f(pcosp,psin)pdpdp D

o A D  i i    i i          i i    i  二、 极坐标系下二重积分的计算 在极坐标系下，如何计算 二重积分 ( , ) D f x y d  极坐标与直角坐标的关系 cos sin x y          f x y f ( , ) ( cos , sin )      d d d      ( , ) ( cos , sin ) D D f x y d f d d           