
第一讲预备知识:线性代数基础 1 线性空间与内积空间 2 向量范数与矩阵范数 3 矩阵特征值 4 矩阵标准型 5几类特殊矩阵 现代数位分析(数位线性代数),潘建瑜 http://math.ecnu.edu.cn/~jypan
第一讲 预备知识:线性代数基础 1 线性空间与内积空间 2 向量范数与矩阵范数 3 矩阵特征值 4 矩阵标准型 5 几类特殊矩阵 现代数值分析(数值线性代数), 潘建瑜 http://math.ecnu.edu.cn/~jypan

1 秦 线性空间与内积空间 ·数域,如:Q,R,C 。线性空间,如:R”,Cn,Rmxn ·线性相关与线性无关,秩,基,维数 ·线性子空间(简称子空间) ·张成子空间:span{x1,c2,,xk} ·像空间(值域,列空间)Ran(A),零空间(核)Ker(A) http://math.ecnu.edu.cn/~jypan 2/28
1 线性空间与内积空间 • 数域, 如: Q, R, C • 线性空间, 如: R n , C n , R m×n • 线性相关与线性无关, 秩, 基, 维数 • 线性子空间 (简称子空间) • 张成子空间: span{x1, x2, . . . , xk} • 像空间 (值域, 列空间) Ran(A), 零空间 (核) Ker(A) http://math.ecnu.edu.cn/~jypan 2/28

秦 2 向量范数与矩阵范数 向量范数 定义(向量范数)若孟数f:Cn→R满足 (1)f(x)≥0,Hx∈C”,等号当且仅当x=0时成立; (2)f(ax)=la·f(x,Hx∈C",a∈C 3)f(x+y)≤f(x)+f(y),x,y∈C”; 则称f(x)为Cm上的范数,通常记作‖·川 白相类似地,我们可以定义实数空间R”上的向量范数. http://math.ecnu.edu.cn/~jypan 3/28
2 向量范数与矩阵范数 向量范数 定义 (向量范数) 若函数 f : C n → R 满足 (1) f(x) ≥ 0, ∀ x ∈ C n , 等号当且仅当 x = 0 时成立; (2) f(αx) = |α| · f(x), ∀ x ∈ C n , α ∈ C; (3) f(x + y) ≤ f(x) + f(y), ∀x, y ∈ C n ; 则称 f(x) 为 C n 上的范数, 通常记作 ∥ · ∥ ✍ 相类似地, 我们可以定义实数空间 R n 上的向量范数. http://math.ecnu.edu.cn/~jypan 3/28
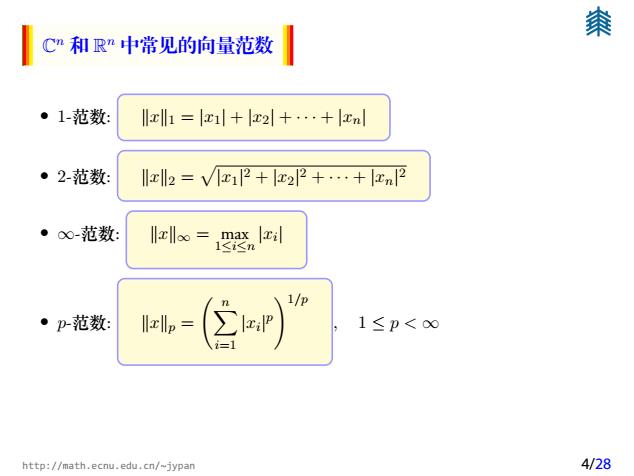
秦 Cn和Rn中常见的向量范数 ·1-范数 x1=z+z2+…+zl ·2-范数 lx2=Vz12+22+…+zn2 ·o-范数: ∞=器 。p范数 1≤p<∞ 1 http://math.ecnu.edu.cn/~jypan 4/28
C n 和 R n 中常见的向量范数 • 1范数: ∥x∥1 = |x1| + |x2| + · · · + |xn| • 2范数: ∥x∥2 = p |x1| 2 + |x2| 2 + · · · + |xn| 2 • ∞范数: ∥x∥∞ = max 1≤i≤n |xi | • p范数: ∥x∥p = Xn i=1 |xi | p !1/p , 1 ≤ p < ∞ http://math.ecnu.edu.cn/~jypan 4/28

秦 向量范数的等价性 定理C”空间上的所有向量范数都是等价的,特别地,有 lx2≤lz1≤√元lxl2 llzlloo≤lz2≤√元lxlo, llalloo≤lxl1≤n alloo. (证明留作练习) 任意有限维赋范线性空间上的所有范数都是等价的 http://math.ecnu.edu.cn/~jypan 5/28
向量范数的等价性 定理 C n 空间上的所有向量范数都是等价的, 特别地, 有 ∥x∥2 ≤ ∥x∥1 ≤ √ n ∥x∥2, ∥x∥∞ ≤ ∥x∥2 ≤ √ n ∥x∥∞, ∥x∥∞ ≤ ∥x∥1 ≤ n ∥x∥∞. (证明留作练习) ✍ 任意有限维赋范线性空间上的所有范数都是等价的 http://math.ecnu.edu.cn/~jypan 5/28

秦 内积与范数 定理(Cauchy-Schwartz不等式) 设(,)是C”上的内积,则对任意x,y∈C,有 I(,2≤(e,x)·(g, (板书) 推论设(,)是C”上的内积,则 lxll≌V(c,x) 是一个向量范数 (证明留作练习)》 http://math.ecnu.edu.cn/~jypan 6/28
内积与范数 定理 (CauchySchwartz 不等式) 设 (·, ·) 是 C n 上的内积, 则对任意 x, y ∈ C n , 有 |(x, y)| 2 ≤ (x, x) · (y, y) (板书) 推论 设 (·, ·) 是 C n 上的内积, 则 ∥x∥ ≜ p (x, x) 是一个向量范数. (证明留作练习) http://math.ecnu.edu.cn/~jypan 6/28

秦 矩阵范数 定义(矩阵范数)若函数f:Cn×m→R满足 (1)f(A)≥0,HA∈Cnxm,等号当且仅当A=0时成立;(非负性) (②)f(aA)=la·f(A),HA∈Cmxm,a∈C:(正齐次性) (3)f(A+B)≤f(A)+(B),HA,B∈Cmxn;(三角不等式) (4)f(AB)≤f(A)f(B),HA,B∈Cnxm 则称f(x)为Cmxn上的(相容)矩阵范数,通常记作‖·【 么若未明确指出,本讲义所涉及矩阵范数都指相容矩阵范数。 http://math.ecnu.edu.cn/~jypan 7/28
矩阵范数 定义 (矩阵范数) 若函数 f : C n×n → R 满足 (1) f(A) ≥ 0, ∀ A ∈ C n×n , 等号当且仅当 A = 0 时成立; (非负性) (2) f(αA) = |α| · f(A), ∀ A ∈ C n×n , α ∈ C; (正齐次性) (3) f(A + B) ≤ f(A) + f(B), ∀A, B ∈ C n×n ; (三角不等式) (4) f(AB) ≤ f(A)f(B), ∀ A, B ∈ C n×n 则称 f(x) 为 C n×n 上的(相容)矩阵范数, 通常记作 ∥ · ∥. ✍ 若未明确指出, 本讲义所涉及矩阵范数都指 相容矩阵范数。 http://math.ecnu.edu.cn/~jypan 7/28
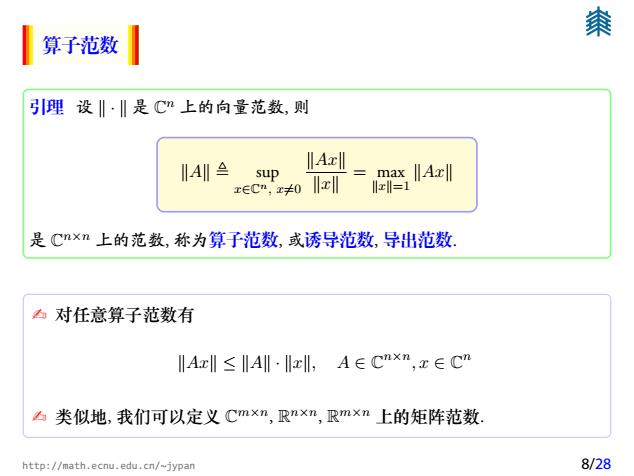
秦 算子范数 引理设‖·‖是C”上的向量范数,则 IAI≌ sup IIAzII ecn,x≠0‖x =max‖Axl x=1 是Cn×n上的范数,称为算子范数,或诱导范数,导出范数 白对任意算子范数有 lAz‖≤A‖·lxl,A∈Cnxm,x∈Cn 类似地,我们可以定义Cm×n,Rn×n,Rmxm上的矩阵范数. http://math.ecnu.edu.cn/~jypan 8/28
算子范数 引理 设 ∥ · ∥ 是 C n 上的向量范数, 则 ∥A∥ ≜ sup x∈Cn, x̸=0 ∥Ax∥ ∥x∥ = max ∥x∥=1 ∥Ax∥ 是 C n×n 上的范数, 称为算子范数, 或诱导范数, 导出范数. ✍ 对任意算子范数有 ∥Ax∥ ≤ ∥A∥ · ∥x∥, A ∈ C n×n , x ∈ C n ✍ 类似地, 我们可以定义 C m×n , R n×n , R m×n 上的矩阵范数. http://math.ecnu.edu.cn/~jypan 8/28
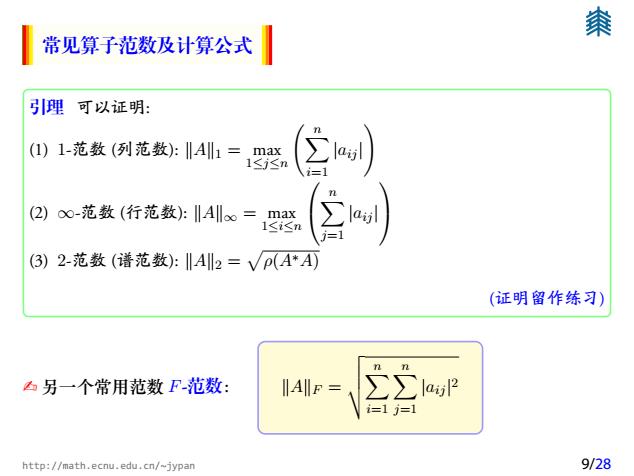
秦 常见算子范数及计算公式 引理可以证明: (1)1-范数(列范数):‖Al1= max 1≤j≤n (2)o0-范数(行范数:A‖=max 1≤i≤m (3)2-范数(谱范数):‖Al2=Vp(A*A) (证明留作练习) nn 山另一个常用范数F-范数: IA‖F= ∑∑la i=1j=1 http://math.ecnu.edu.cn/~jypan 9/28
常见算子范数及计算公式 引理 可以证明: (1) 1范数 (列范数): ∥A∥1 = max 1≤j≤n Xn i=1 |aij | ! (2) ∞范数 (行范数): ∥A∥∞ = max 1≤i≤n Xn j=1 |aij | (3) 2范数 (谱范数): ∥A∥2 = p ρ(A∗A) (证明留作练习) ✍ 另一个常用范数 F范数: ∥A∥F = vuut Xn i=1 Xn j=1 |aij | 2 http://math.ecnu.edu.cn/~jypan 9/28

秦 矩阵范数的等价性 定理定义在Rm×n上的所有范数都是等价的,特别地,有 A2≤4≤VA2, 1 A业≤4s≤VaA2, 1 方4s≤IA:≤nlAe, 点4h≤IAe≤va4 (证明留作练习) http://math.ecnu.edu.cn/~jypan 10/28
矩阵范数的等价性 定理 定义在 R n×n 上的所有范数都是等价的, 特别地, 有 1 √ n ∥A∥2 ≤ ∥A∥1 ≤ √ n ∥A∥2, 1 √ n ∥A∥2 ≤ ∥A∥∞ ≤ √ n ∥A∥2, 1 n ∥A∥∞ ≤ ∥A∥1 ≤ n ∥A∥∞, 1 √ n ∥A∥1 ≤ ∥A∥F ≤ √ n ∥A∥2. (证明留作练习) http://math.ecnu.edu.cn/~jypan 10/28