第八章多元函数微分法及其应用 多元函数的概念 主要内容 多元函数的偏导数 多元函数的全微分 多元函数的求导法则 多元函数微分法的应用
多元函数的概念 多元函数的偏导数 多元函数的全微分 多元函数的求导法则 主 要 内 容 多元函数微分法的应用 第八章 多元函数微分法及其应用
第一节多元函数的基本概念 平面点 桌与区域 多元函数 多元函数 的极限 的连续性 多元函数 的概念 Ooo⊙o8
平面点 集与区域 多元函数 的概念 多元函数 的极限 多元函数 的连续性 机动 目录 上页 下页 返回 结束 第一节 多元函数的基本概念

平面点集与区域 平面点集:平面上具有某种性质的点的集合 1.邻域:平面上与点(x,)距离小于6>0的点P(x,y)的全体称为点(x)的邻域 U(B.5)=(P:RPI<6)=(x.)x-x)+(y-y<6 内点 2.去心邻域:U(,)={P:0<P<δ} 边界点 3.内点:设E是平面上的一个点集.如果存在点P的邻域U(P),使得UP)∈E,则称点 P叫做为点集E的内点 4,边界点:如果点P的任意邻域中就有E的内点又有不属于E的点.,则称 P叫做为点集E的.边界点
平面点集:平面上具有某种性质的点的集合 1.邻域:平面上与点 0 0 0 P x y ( , )距离小于 0的点 P x y ( , ) 的全体称为点 0 0 0 P x y ( , )的邻域 2 2 0 0 0 0 U P P P P x y x x y y ( , ) : ( , ) ( ) ( ) 一、 平面点集与区域 2.去心邻域: U P P PP ( , ) : 0 0 0 3.内点:设 E 是平面上的一个点集.如果存在点 P 的邻域U P( ),使得U P E ( ) ,则称点 P 叫做为点集 E 的内点. E P P 内 点 4.边界点:如果点 P 的任意邻域中就有 E 的内点又有不属于 E 的点.,则称 P 叫做为点集 E 的.边界点. 边界点
平面点集与区域 5.开集:如果点集E的每一个点都是它的内点,则称点集E为开集, E={x,y)l<x2+y2<4} 6.连通:如果对开集D内的任意两点都可以用完全位于D内的折线 连接起来,则称开集D是连通的. 7. 开区域:连通的开集成为(开)区域 8. 闭区域:(开)区域连同它的边界点 E={x,y)l≤x2+y2≤4 9.有界点集:如果平面集E可以含于某个以原点为圆心的圆内,则称E为有界点集 否则称E为无界点集
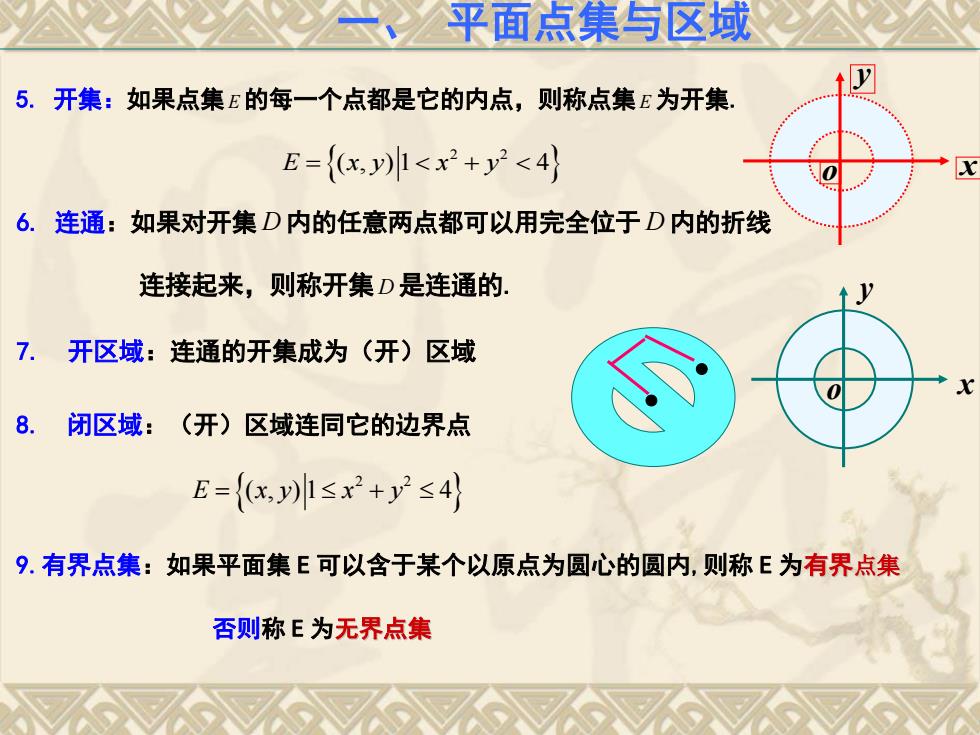
5. 开集:如果点集E的每一个点都是它的内点,则称点集E 为开集. 2 2 E x y x y ( , ) 1 4 6. 连通:如果对开集 D 内的任意两点都可以用完全位于 D 内的折线 连接起来,则称开集D是连通的. x y o 7. 开区域:连通的开集成为(开)区域 8. 闭区域:(开)区域连同它的边界点 2 2 E x y x y ( , ) 1 4 x y o 9.有界点集:如果平面集 E 可以含于某个以原点为圆心的圆内,则称 E 为有界点集 否则称 E 为无界点集 一、 平面点集与区域

二、多元函数的基本概念 背景:圆柱体体积V和它的底半径r、高h之间具有关系V=πr2h V=πr.2h的特点是什么? (1) 有三个变量,其中两个自变量,一个因变量 (2) 当两个自变量在某一范围内取值时,因变量通过某 一对应法则 有唯一值和它对应 定义1:设有三个变量x,y,z,如果当变量在一定范围内任意取定一对值(x,y)时 变量z按照一定的法则总有唯一确定的值与之对应,则称这个对应 法则f为x,y的二元函数.记作z=f(xy)=f(P),P(x,y) Z叫做因变量 x,y叫做自变量 自变量x,y的变化范围称为二元函数的定义域
背景:圆柱体体积 V 和它的底半径 r、高 h 之间具有关系 V= 2 r h V= 2 r h 的特点是什么 ? (1) 有三个变量,其中两个自变量,一个因变量 (2) 当两个自变量在某一范围内取值时,因变量通过某 一对应法则 二、 多元函数的基本概念 有唯一值和它对应 定义 1:设有三个变量 x y z , , ,如果当变量在一定范围内任意取定一对值( , ) x y 时 变量 z 按照一定的法则 f 总有唯一确定的值与之对应,则称这个对应 法则 f 为 x, y 的二元函数. 记作 z f x y f P P x y ( , ) ( ), ( , ) z 叫做因变量 x y, 叫做自变量 自变量 x, y 的变化范围称为二元函数的定义域

多元函数的基本概念 背景:圆柱体体积V和它的底半径r、高h之间具有关系V=πr2h V=πr.2h的特点是什么? (1) 有三个变量,其中两个自变量,一个因变量 (2) 当两个自变量在某一范围内取值时,因变量通过某一对应法则 有唯一值和它对应 定义1:设有三个变量x,y,z,如果当变量在一定范围内任意取定一对值(x,y)时 变量z按照一定的法则∫总有唯一确定的值与之对应,则称这个对应 法则f为x,y的二元函数.记作z=f(xy)=f(P),P(x,y) 2叫做因变量 x,y叫做自变量 自变量x,y的变化范围称为二元函数的定义域
背景:圆柱体体积 V 和它的底半径 r、高 h 之间具有关系 V= 2 r h V= 2 r h 的特点是什么 ? (1) 有三个变量,其中两个自变量,一个因变量 (2) 当两个自变量在某一范围内取值时,因变量通过某一对应法则 二、 多元函数的基本概念 有唯一值和它对应 定义 1:设有三个变量 x y z , , ,如果当变量在一定范围内任意取定一对值( , ) x y 时 变量 z 按照一定的法则 f 总有唯一确定的值与之对应,则称这个对应 法则 f 为 x, y 的二元函数. 记作 z f x y f P P x y ( , ) ( ), ( , ) z 叫做因变量 x y, 叫做自变量 自变量 x, y 的变化范围称为二元函数的定义域
、多元函数的基本概念 注记1:二元函数z=fxy)的定义是一元函数y=f(x)定义的推广 注记2:二元函数z=f(x,y)与一元函数y=f(x)定义的差异 (1)二元函数涉及到三个变量x,y,z,其中两个自变量,一个因变量 一元函数涉及到两个变量x,y,其中一个自变量,一个因变量 (2)二元函数的定义域是平面点集,一元函数的定义域是数轴上的点集 (3) 二元函数的几何图形是空间曲面,一元函数的几何图形是平面曲线 f(x,)
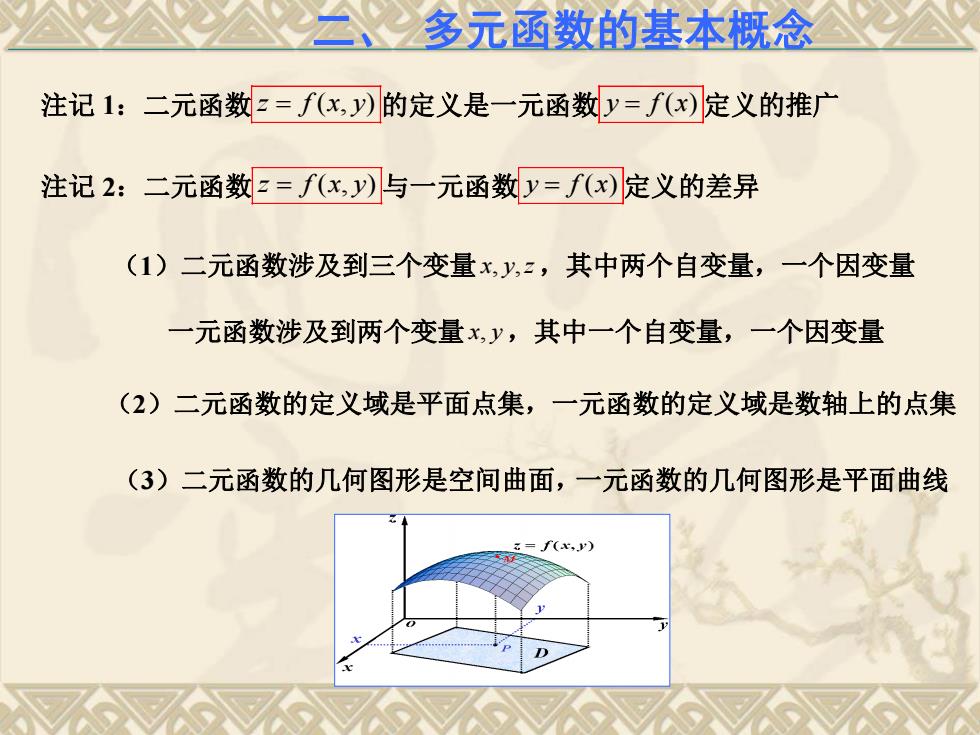
注记 1:二元函数 z f (x, y) 的定义是一元函数 y f x ( ) 定义的推广 注记 2:二元函数 z f (x, y) 与一元函数 y f x ( ) 定义的差异 二、 多元函数的基本概念 (1)二元函数涉及到三个变量 x y z , , ,其中两个自变量,一个因变量 一元函数涉及到两个变量 x y, ,其中一个自变量,一个因变量 (2)二元函数的定义域是平面点集,一元函数的定义域是数轴上的点集 (3)二元函数的几何图形是空间曲面,一元函数的几何图形是平面曲线

多元函数的基本概念 例1:试确定下列函数的定义域 因此z=arcsin(x2+y2)的定义域为 (1)z=In(x+y) D={x,)川x2+y2≤1 (2)==arcsin(x2+y2) 课堂训练1:试确定下列函数的定义域 解:(1)要使z=ln(x+y)有意义 (1)2=ln(1-2x+y2) 必须满足x+y>0 因此z=ln(x+y)的定义域为 (2)+y x-y D={x,y川x+y>0} (3)=1+1 (2)要使z=arcsin(x2+y2)有意义 必须满足x2+y2≤1 (4)z=arccos x+y
二、 多元函数的基本概念 例 1: 试确定下列函数的定义域 (1) z x y ln (2) 2 2 z x y arcsin 解:(1)要使 z x y ln 有意义 必须满足 x y 0 因此 z x y ln 的定义域为 D x y x y ( , ) 0 (2)要使 2 2 z x y arcsin 有意义 必须满足 2 2 x y 1 因此 2 2 z x y arcsin 的定义域为 2 2 D x y x y ( , ) 1 课堂训练 1: 试确定下列函数的定义域 (1) 2 z x y ln 1 2 (2) 1 1 z x y x y (3) 1 1 1 u x y z (4) 2 2 arccos z z x y

三、多元函数的极限△ 回顾1:数轴上动点Mx)趋于定点M,(x)1:平面上动点P(x,)趋于定点B(x,)定义 若MM-→0,则M(x)→M() 若BP→0,则P(x,)→E(%) 回顾2:m)=A的描述定义 2:Px,)→B(x,)时fx,y)→A的定义 (1)函数fx)在点x,的去心领域有意义 (1)函数fx,)在B(x,)的附近有意义 (2)自变量x在该去心邻域内任意地接 (2)当Px,)沿任意的路径无限接近B(x,)时 近于x,(或说趋于)时,fx)总 fx,)总无限的接近一个固定的数4,记作 无限的接近一个固定的数A lim f(x,y)=A 回顾3:imfx)=A的精确定义 -o 对给定的8>0,总3δ>0, 对给定的8>0,总38>0, 当0<PP<δ时都有fx,)-A<e 当0<x-x<时都有fx)-A<ε
三、 多元函数的极限 回顾 1:数轴上动点M x( )趋于定点 0 0 M x( ) 若 0 M M 0,则 M x( ) 0 0 M x( ) 回顾 2: f x A x x lim ( ) 0 的描述定义 (1)函数 f x( )在点 0 x 的去心领域有意义 (2)自变量x在该去心邻域内任意地接 近于 0 x (或说趋于 0 x )时, f x( )总 无限的接近一个固定的数 A 回顾 3: f x A x x lim ( ) 0 的精确定义 对给定的 0,总 0, 0 当0 x x 时都有 f x A ( ) 1:平面上动点P x y ( , )趋于定点 0 0 0 P x y ( , )定义 若 0 P P 0,则 P x y ( , ) 0 0 0 P x y ( , ) 2:P x y ( , ) 0 0 0 P x y ( , )时 f x y A ( , ) 的定义 (1)函数 f x y ( , )在 0 0 0 P x y ( , )的附近有意义 (2)当P x y ( , )沿任意的路径无限接近 0 0 0 P x y ( , )时 f x y ( , )总无限的接近一个固定的数 A,记作 0 0 ( , ) ( , ) lim ( , ) x y x y f x y A 对给定的 0,总 0, 0 当0 P P 时都有 f x y A ( , )

多元函数的极限 (1)Px)→(x),意味着点B,P的 (1)x→,意味着点x,。 的距离 距离任意小,也即Vx-)+y-充 任意小,也即x-x充分小即 分小即0<Vx-x)2+(y-)2<6 即 0<x-x<δ (2)Px,)趋于B,(x,)是指沿任意的路径 (2)X趋于x,的路径只有两条 无限接近而不是沿某些路径无限接近. X从x,的左右两则趋于x (3)判断吧x川=4不存在的方法 (3)判断四x,)=4不存在的方法 找两种(x)→(x)不同趋近方式, 当点P(x,y)沿直线y=趋于点(x%)时 使.四少)存在但两者不相等 lim,f(x,y)存在但与k有关
三、 多元函数的极限 (1)P x y ( , ) 0 0 0 P x y ( , ),意味着点 0 P P, 的 分小即 2 2 0 0 0 ( ) ( ) x x y y 距离任意小,也即 2 2 0 0 ( ) ( ) x x y y 充 (1)x 0 x ,意味着点 0 x x, 的距离 即 0 0 x x 任意小,也即 0 x x 充分小即 (2)P x y ( , )趋于 ( , ) 0 0 0 P x y 是指沿任意的路径 无限接近而不是沿某些路径无限接近. (2) x 趋于 0 x 的路径只有两条 x 从 0 x 的左右两则趋于 0 x (3)判断 0 0 ( , ) ( , ) lim ( , ) x y x y f x y A 不存在的方法 找两种 0 0 ( , ) ( , ) x y x y 不同趋近方式, 使 0 0 ( , ) ( , ) lim ( , ) x y x y f x y 存在但两者不相等 (3)判断 0 0 ( , ) ( , ) lim ( , ) x y x y f x y A 不存在的方法 当点 P x y ( , ) 沿直线 y kx 趋于点 0 0 0 P x y ( , )时 0 0 ( , ) ( , ) lim ( , ) x y x y f x y 存在但与k 有关