
第五章 定积分及其应用 主要内容: 一、定积分的概念与性质 二、微积分基本公式 三、定积分的求法 四、定积分的应用
第五章 定积分及其应用 主要内容: 一、定积分的概念与性质 二、微积分基本公式 三、定积分的求法 四、定积分的应用
§5.1 定积分的概念与性质 定积分的 定义 问题的提出 定积分的 主要内容 几何意义 定积分的 性质 定积分的 应用
主要内容 问题的提出 定积分的 定义 定积分的 性质 定积分的 几何意义 定积分的 应用 §5.1 定积分的概念与性质 5.1
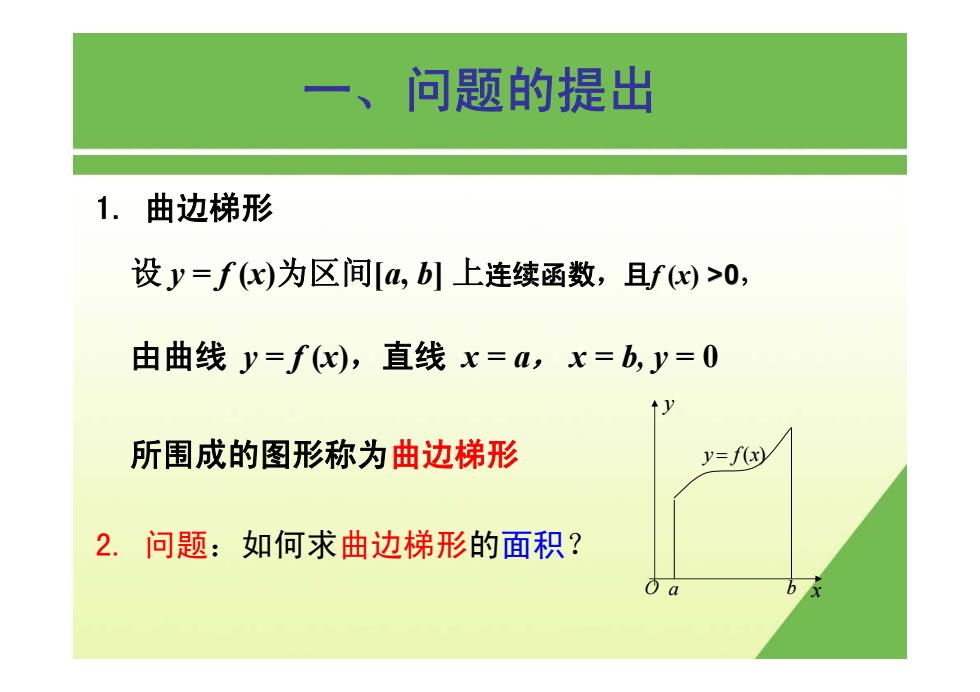
一、问题的提出 1.曲边梯形 设y=f(x)为区间,b]上连续函数,且f)>0, 由曲线y=fx),直线x=,x=b,y=0 所围成的图形称为曲边梯形 y=f(x) 2.问题:如何求曲边梯形的面积? 0 a
一、问题的提出 1. 曲边梯形 设 y = f (x)为区间[a, b] 上连续函数,且f (x) >0, 由曲线 y = f (x),直线 x = a, x = b, y = 0 所围成的图形称为曲边梯形 2. 问题:如何求曲边梯形的面积? x y O a b y = f(x)
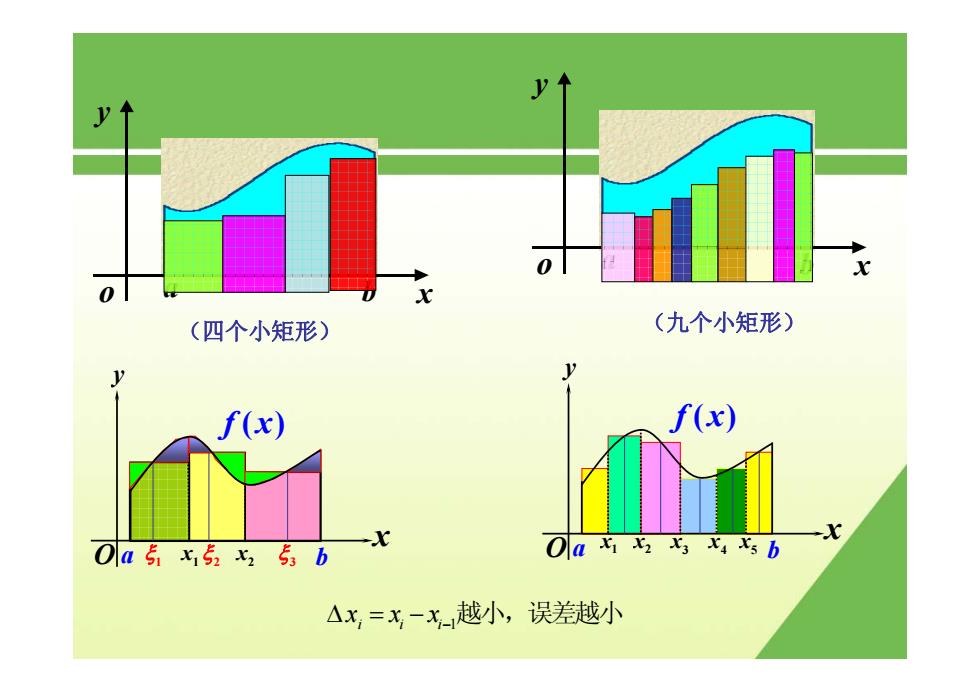
0 (四个小矩形) (九个小矩形) f(x) f(x) Oa5x5x2 5 b Oax x2 x3 Xsxs b △x,=X一x越小,误差越小
a b x y o (四个小矩形) a b x y o (九个小矩形) x y O a b f ( ) x 1 x 1 ξ 2 x 2 ξ 3 ξ x y O a b f ( ) x 1 x 5 x2 x 3 x 4 x i ii 1 x xx Δ = − − 越小,误差越小
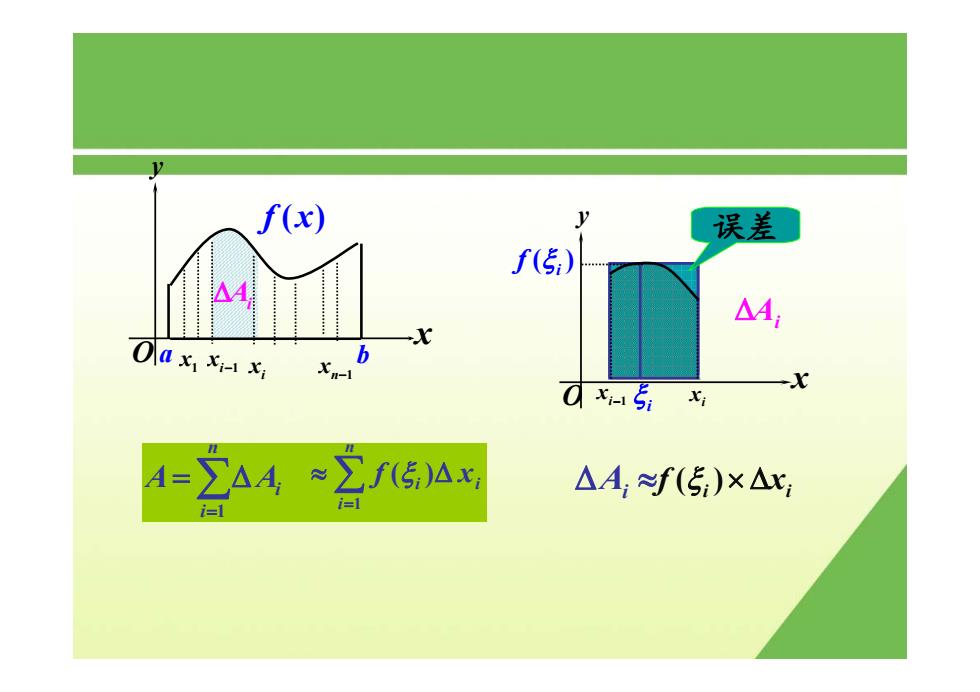
f(x) y 误差 f(5) △4 △4 Oaxxixi 七,b 0x15i9 A=2A4=25)A △A:≈f(5:)×△x
x y O a b f x( ) 1 x n x −1 i 1 x − i x x y O i 1 x − i x i ξ ( )i f ξ ( )i i f x ξ × Δ 误差 ΔAi ∑ = = Δ n i A Ai 1 ΔAi ≈ ΔAi ∑ = ≈ Δ n i i xi f 1 (ξ )
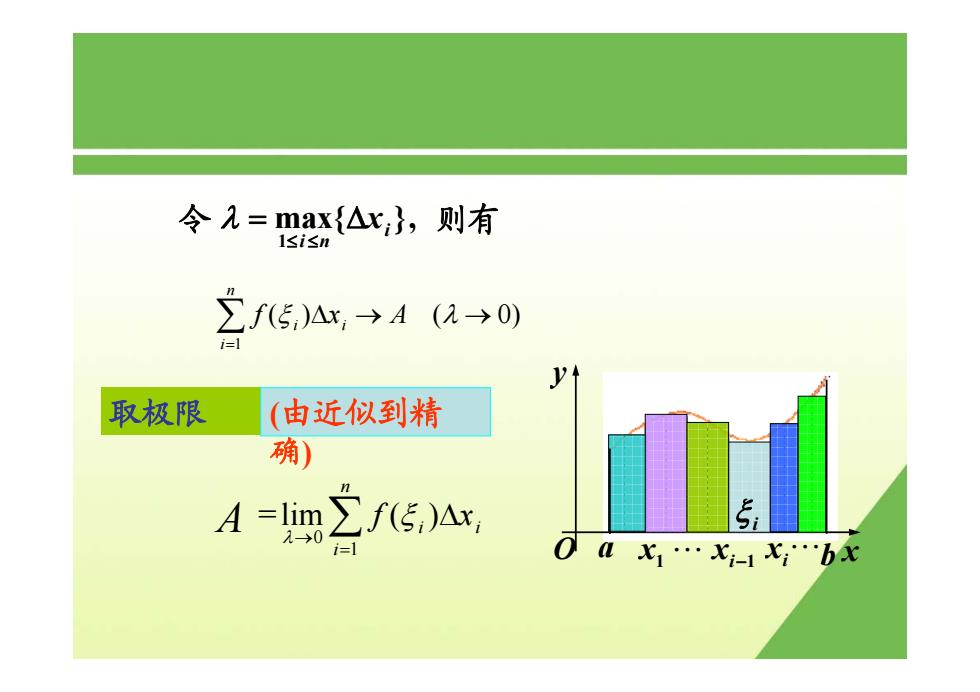
令九=max{△x,},则有 I<i<n f,Ax→A(a→0) i-l 取极限 (由近似到精 确)】 A=m∑,, i=1 O0K1…X-1x:bx
取极限 令 max{ }, 1 i i n = Δx ≤ ≤ λ 则有 0 1 = lim ( ) n i i i f x λ ξ → = ∑ Δ a b x y O 1 x xi−1 xi ξ i " " (由近似到精 确) A 1 ( ) ( 0) n i i i f xA ξ λ = ∑ Δ→ →

二、定积分的定义 设函数fxw)在[a,b]上有界 在[a,b]中任意插入若干个分点 a=X0<x<…<x-l<X,<…<Xn-1<xn=b 将区间[a,b1划分为n个小区间xx]各个小区间的长度依次为△x,=x,-x- 在每个小区间[x-,x,]上任取一点5,作乘积f(5)△x(i=1,2,,n),并求和 s,-()Ax 记A=m2xA} 如果不论对区间[a,]怎样划分,也不论∈[x-x]怎样选取,只要→0时, mS,=m2传)△y总存在都为】 = 则称1为fx)在[a,b1上的定积分,记为∫fx=1=lim∑f(传)△x
设函数 f ( ) x 在[,] a b 上有界 二、定积分的定义 在[,] a b 中任意插入若干个分点 01 1 1 ii nn ax x x x x x b = <<< <<< < = " " − − 将区间[,] a b 划分为n 个小区间 1 [ ,] i i x x − 各个小区间的长度依次为 i ii 1 x x x Δ = − − 在每个小区间 1 [ ,] i i x x − 上任取一点 i ξ ,作乘积 ( )i i f ξ Δx (i n =1, 2, , " ),并求和 1 ( ) n n ii i S fx ξ = = ∑ Δ 记 1 max{ }i i n λ x ≤ ≤ = Δ 如果不论对区间[,] a b 怎样划分,也不论 1 [ ,] i ii ξ x x ∈ − 怎样选取,只要λ → 0时, 0 0 1 lim lim ( ) n n ii i S fx λ λ ξ → → = = ∑ Δ 总存在都为I 则称I 为 f ( ) x 在[,] a b 上的定积分,记为 0 1 ( ) lim ( ) n b i i a f x dx I f x λ ξ → ∫ == Δ ∑
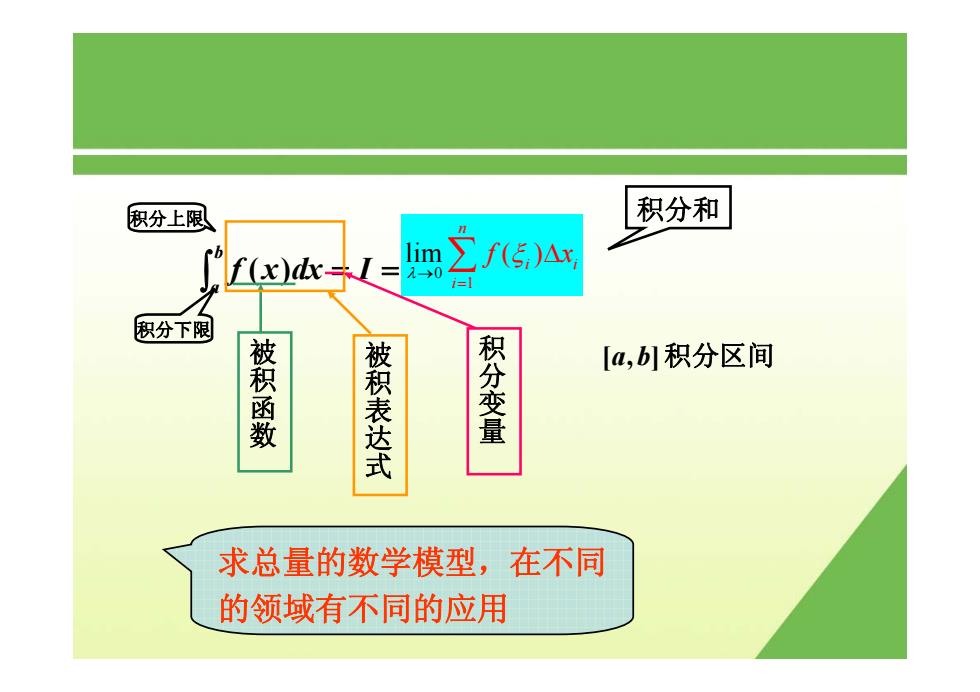
积分上限 积分和 b f(x)dxI=0 lim∑f(5)△x i=l 积分下限 积函数 被积表达式 积分变量 [a,b]积分区间 求总量的数学模型,在不同 的领域有不同的应用
∫ = = ba f ( x)dx I 1 0 l mi ( ) n i i i f x λ ξ = → ∑ Δ 被积函数 被积表达式 积分变量 [a,b]积分区间 积分上限 积分下限 积分和 求总量的数学模型,在不同 的领域有不同的应用

比较 定积分 不定积分 (1)定积分∫fx本是-个数量. (1)不定积分」f(x)是f(x)的所有原函数 2) 定积分∫fx本只与被积函数fx)及 (2)不定积分「fx)d只与被积函数f(x 积分区间[a,b]有关,与积分变量记号无关 和积分变量记号有关: 即j。fa-jfua=jfeh 即:若∫f(x)d=F(x)+C,则 ∫fu)dM=F()+C
比 较 定积分 不定积分 (1) 定积分 () b a f x dx ∫ 是一个数量. (1)不定积分 f ( ) x dx ∫ 是 f ( ) x 的所有原函数 (2) 定积分 () b a f x dx ∫ 只与被积函数 f ( ) x 及 积分区间[,] a b 有关,与积分变量记号无关 即 ( ) b a f x dx ∫ ( ) () b b a a = = f u du f t dt ∫ ∫ (2) 不定积分 f ( ) x dx ∫ 只与被积函数 f (x) 和积分变量记号有关. 即: 若 f () () x dx F x C = + ∫ ,则 f () () u du F u C = + ∫
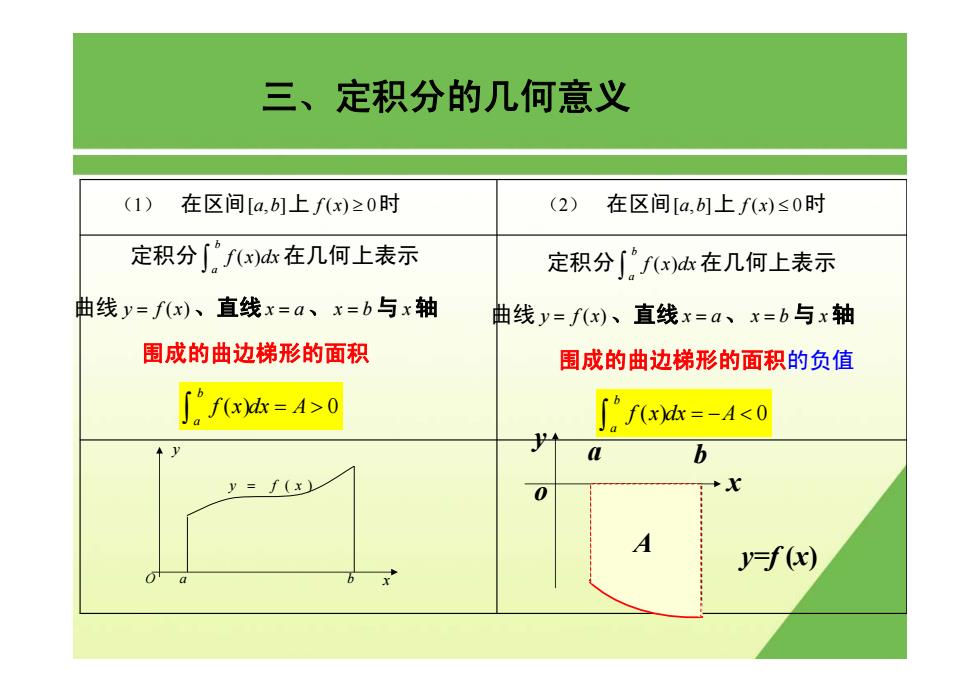
三、定积分的几何意义 (1) 在区间[a,1上fx)≥0时 (2) 在区间[a,1上fx)≤0时 定积分∫fx)在几何上表示 定积分∫fx)d在几何上表示 曲线y=fx)、直线x=a、x=b与x轴 曲线y=fx)、直线x=a、x=b与x轴 围成的曲边梯形的面积 围成的曲边梯形的面积的负值 ∫2f=A0 f=-A0 e b y=f(x) 0 →X A yf(x)
(1) 在区间[,] a b 上 f x() 0 ≥ 时 三、定积分的几何意义 定积分 ( ) b a f x dx ∫ 在几何上表示 曲线 y fx = ( )、直线 x a = 、 x b = 与 x轴 围成的曲边梯形的面积 () 0 b a f x dx A = > ∫ x y O a b y = f ( x ) (2) 在区间[,] a b 上 f x() 0 ≤ 时 定积分 ( ) b a f x dx ∫ 在几何上表示 曲线 y fx = ( )、直线 x a = 、 x b = 与 x轴 围成的曲边梯形的面积的负值 () 0 b a f x dx A = − < ∫ o x y a b y=f (x) A