
第四节线性多步法 一、多步法的基本思想 二、线性多步法 三、小结
第四节 线性多步法 一、多步法的基本思想 二、线性多步法 三、小结

一、多步法的基本思想 前面介绍的几种方法都是单步法,即在计算时,仅用它 前面一步得到的信息%,设想,当通过单步法已经算 出 y,y-…yk如何能充分地利用这些信息,在计算 y时获得较高的精度,这就是多步法的基本思想
一、多步法的基本思想 前面介绍的几种方法都是单步法,即在计算时,仅用它 前面一步得到的信息 。设想,当通过单步法已经算 出 ,如何能充分地利用这些信息,在计算 时获得较高的精度,这就是多步法的基本思想。 n y n n n k y y y − − , , 1 n+1 y

二、线性多步法 假定仍讨论本章开始给出的二阶微分方程的初值 问题(1.1)、(1.2》 y'=f(x,) y(xo)=Yo 与其等价的积分方程是 xm)-x,)=fx,x》k (4.1) 前面我们曾使用梯形公式,计算(4.1)式右端的积分,而得 到了改进的Euler方法。其实,这也可以理解为是插值点xn和 xm+,的线性插值函数代替函数∫而得到的。由于通常插值多项 式的次数越高越精确,所以使我们试图用高次插值多项式代替∫, 来得到高精确的计算方法
假定仍讨论本章开始给出的一阶微分方程的初值 问题(1.1)、(1.2) = = 0 0 ( ) ( , ) y x y y f x y 与其等价的积分方程是 (4.1) + + − = 1 ( ) ( ) ( , ( )) 1 n n x x n n y x y x f x y x dx 前面我们曾使用梯形公式,计算(4.1)式右端的积分,而得 到了改进的Euler方法。其实,这也可以理解为是插值点 和 的线性插值函数代替函数 而得到的。由于通常插值多项 式的次数越高越精确,所以使我们试图用高次插值多项式代替 , 来得到高精确的计算方法。 n x n+1 x f f 二、线性多步法

今取xn-2,xm-,xn和xm+1为插值节点,这时的插值多项式为 P(x)= (x-xn(x-xn-1x-x2) f(y()) (xn41-Xnx1-X-(xn+-xn2 +-xx=-x-x-)j0xx》 (n-x+)(nx1)(Xn-xn-2) x-(x-x)(x-x-2) 十 ()(x)(2) fxx2》 +(-Xx-xx-x2) fxn-2,-2》 (n-2-)(Xn-2-x)n-2-X-) 用(x代替f(x,yx》,便得到(x)的近似值y+,即 y=x)+∫R(x)
今取 xn−2 , xn−1 , xn 和 xn+1 为插值节点,这时的插值多项式为 ( , ( )) ( )( )( ) ( )( )( ) ( , ( )) ( )( )( ) ( )( )( ) ( , ( )) ( )( )( ) ( )( )( ) ( ) 1 1 1 1 1 1 2 1 2 1 1 2 1 1 2 1 1 1 1 1 1 2 1 2 3 − − − + − − − + − + − − + − − + + + + − + − − − − − − − − − + − − − − − − + − − − − − − = n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n f x y x x x x x x x x x x x x x f x y x x x x x x x x x x x x x f x y x x x x x x x x x x x x x P x ( , ( )) ( )( )( ) ( )( )( ) 2 2 2 1 2 2 1 1 1 − − − + − − − + − − − − − − − + n n n n n n n n n n n f x y x x x x x x x x x x x x x 用 P3 (x) 代替 f (x, y(x)) ,便得到 y(xn+1 ) 的近似值 yn+1 ,即 + + = + 1 ( ) ( ) 1 3 n n x x yn y xn P x dx

令x=xn+h,并注意到 Xm+lXn=Xn=Xn1-X-2=h 则得 y=,)+后/xu+1m+2d -(u-IYu+1u+2)diu +与xrxu-lu+2dh -言c-2x-月u-lu+1au =.)+249/ax》+19/,》 -5f(xn-1,y(xm-》+f(xm-2,xn-2)川 上式中右端的(x,)用,代替,就有
令 x = xn + uh ,并注意到 xn+1 − xn = xn − xn−1 = xn−1 − xn−2 = h 则得 5 ( , ( )) ( , ( ))] [9 ( , ( )) 19 ( , ( )) 24 1 ( ) ( , ( )) ( 1) ( 1) 6 1 ( , ( )) ( 1) ( 2) 2 1 ( , ( )) ( 1)( 1)( 2) 2 1 ( , ( )) ( 1)( 2) 6 1 ( ) 1 1 2 2 1 1 1 0 2 2 1 0 1 1 1 0 1 0 1 1 1 − − − − + + − − − − + + + − + = + + − − + + − + − − + + = + + + n n n n n n n n n n n n n n n n n n n f x y x f x y x y x h f x y x f x y x hf x y x u u u du hf x y x u u u du hf x y x u u u du y y x hf x y x u u u du 上式中右端的 y(xi ) 用 yi 代替,就有

yay)9f()+19f) 24 (4.2) -5f(xn1,(xn-》+f(x-2,Jy(xn-2) 显然,这是一个隐式方法,称(4.2)式为Adams内插公式。 上面之所以得到的是隐式方法,其原因在于选用了x+作 为插值节点。 我们取xm3,xn-2,x和衡为插值节点。这时的插值 多项式成为 2()=Xx-Xxx) f(xn,xn)》 (xn-Xn-1)(xn-xn-2)(Xn-xn-3) (x-Xnx-xm-2(x-xn-3) (n-1-X)-1-X-2)-1-x3) 、fx1x-》 X》 (x-xnx-xa-x-x-2】
5 ( , ( )) ( , ( ) [9 ( , ) 19 ( , ) 24 1 ( ) 1 1 2 2 1 1 1 − − − − + + + − + = + + n n n n n n n n n n f x y x f x y x y y x h f x y f x y (4.2) 显然,这是一个隐式方法,称(4.2)式为Adams内插公式。 上面之所以得到的是隐式方法,其原因在于选用了 作 为插值节点。 n+1 x 我们取 ,和 作为插值节点。这时的插值 多项式成为 3 2 1 , , n− n− n− x x x n x ( , ( )) ( )( )( ) ( )( )( ) ( , ( )) ( )( )( ) ( )( )( ) ( , ( )) ( )( )( ) ( )( )( ) ( ) 2 2 2 2 1 2 3 1 2 1 1 1 1 2 1 3 2 3 1 2 3 1 2 3 3 − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − + − − − − − − + − − − − − − = n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n f x y x x x x x x x x x x x x x f x y x x x x x x x x x x x x x f x y x x x x x x x x x x x x x P x

(x-xnx-xn-1X-Xm-2】 、f(xn-3,yxm3》 (xn-3-Xnxm-3-xm-ixn-3-Xm-2)〉 用上式代替(4.1)式右端积分中的fx,(x)也将 得到y(xm的近似值ym1与推导隐式方法(4.2)的 过程类似,可得到如下的显式公式: X-*45)-59-) +37f(xn-2,yn-)-9f(xm-3,yn-3】 (4.3) 称(4.3)式为Adamsa外插公式。在讨论它们的截断误差 x)y时,不仅要假定y,=()还要假定 ym-=J(xn1)ym2=y(xn和yn-3=yxn8)容易证明截断 误差均为O(h。)
( , ( )) ( )( )( ) ( )( )( ) 3 3 3 3 1 3 2 1 2 − − − − − − − − − − − − − − − + n n n n n n n n n n n f x y x x x x x x x x x x x x x 用上式代替(4.1)式右端积分中的 ,也将 得到 的近似值 ,与推导隐式方法(4.2)的 过程类似,可得到如下的显式公式: (4.3) f (x, y(x)) ( ) n+1 y x n+1 y 37 ( , ) 9 ( , )] [55 ( , ) 59 ( , ) 24 1 2 1 3 3 1 1 1 − − − − + − − + − = + − n n n n n n n n n n f x y f x y y y h f x y f x y 称(4.3)式为Adams外插公式。在讨论它们的截断误差 时,不仅要假定 ,还要假定 和 ,容易证明截断 误差均为 。 1 1 ( ) n+ − n+ y x y ( ) n n y = y x ( ), ( ) n−1 = n−1 n−2 = n−2 y y x y y x ( ) n−3 = n−3 y y x ( ) 5 O h

例5取步长h=0.1,使用线性多步法求解例1给出的初值问题。 解为了使用线性多步法求解,今先使用R一K方法算 出y,'和3。然后分别使用外插公式以及外插、内插 联合使用的预估校正法计算后面的数值解。 (1) 预估公式(外插公式) y=y+h55f(xy)-59f() 24 +37f(xm-2,ym-2)-9f(xn-3,ym-3月 (2)校正公式(内插公式) y+()+19f() -5f(xn-1yn)+f(x-2,ym-2]
例5取步长 h = 0.1 ,使用线性多步法求解例1给出的初值问题。 解 为了使用线性多步法求解,今先使用R-K方法算 出 和 。然后分别使用外插公式以及外插、内插 联合使用的预估校正法计算后面的数值解。 , 1 y 2 y 3 y (1) 预估公式(外插公式) 37 ( , ) 9 ( , )] [55 ( , ) 59 ( , ) 24 1 2 2 3 3 1 1 (0) 1 − − − − + − − + − = + − n n n n n n n n n n f x y f x y y y h f x y f x y (2)校正公式(内插公式) 5 ( , ) ( , )] [9 ( , ) 19 ( , ) 24 1 1 1 2 2 1 1 1 − − − − + + + − + = + + n n n n n n n n n n f x y f x y y y h f x y f x y
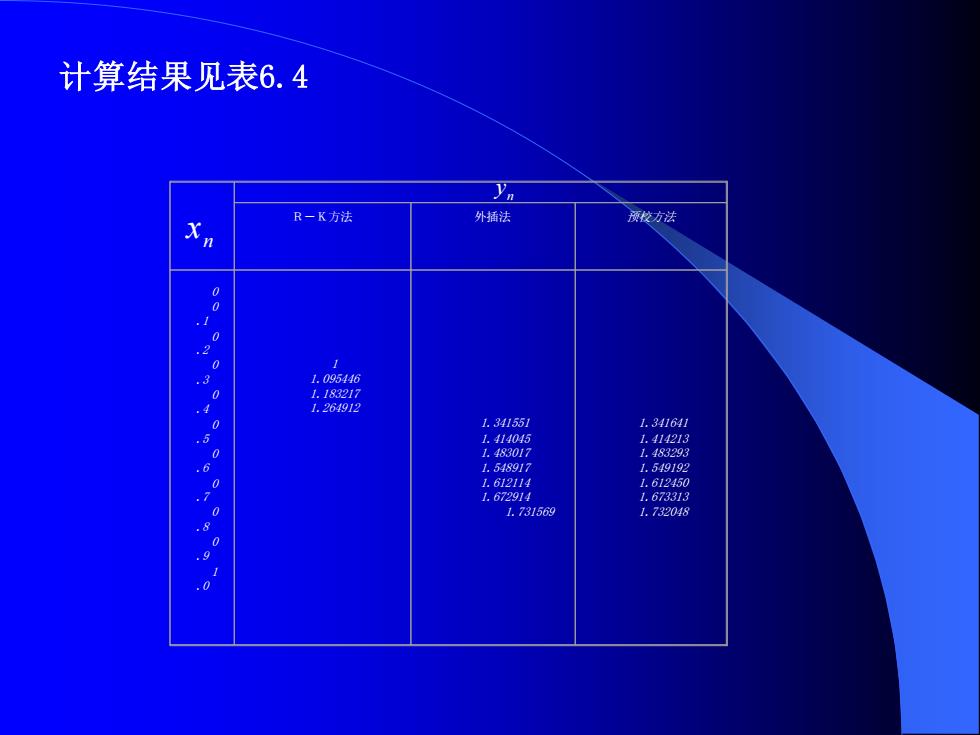
计算结果见表6.4 R一K方法 外插法 预牧方法 0 2 1.095446 1.183217 1.264912 1.341551 1.34164 1.414045 1.414213 1.483017 1.483293 1.54891/ 1.549192 L.612114 1.612450 1.672914 1.673313 1.731569 1.732048 .0
计算结果见表6.4 n x n y R-K方法 外插法 预校方法 0 0 .1 0 .2 0 .3 0 .4 0 .5 0 .6 0 .7 0 .8 0 .9 1 .0 1 1.095446 1.183217 1.264912 1.341551 1.414045 1.483017 1.548917 1.612114 1.672914 1.731569 1.341641 1.414213 1.483293 1.549192 1.612450 1.673313 1.732048

三、小结 1、多步法的基本思想 2、线性多步法 Adams内插公式 =,)+249fa)+19fy) (4.2) -5f(xnxn》+f(xn2,xm2) Adams外插公式 y=+2455/3.)-59f1y.) +37f(xn-2,yn-)-9f(xm-3,ym-3]
1、多步法的基本思想 5 ( , ( )) ( , ( ) [9 ( , ) 19 ( , ) 24 1 ( ) 1 1 2 2 1 1 1 − − − − + + + − + = + + n n n n n n n n n n f x y x f x y x y y x h f x y f x y (4.2) Adams内插公式 37 ( , ) 9 ( , )] [55 ( , ) 59 ( , ) 24 1 2 1 3 3 1 1 1 − − − − + − − + − = + − n n n n n n n n n n f x y f x y y y h f x y f x y Adams外插公式 2、线性多步法 三、小结