
3-31 复化求积公式 一、引言 二、复化梯形公式
3-3 复化求积公式 一、引言 二、复化梯形公式

一、引言 由于高阶的Newton-Cotes公式不宜使用,而在比较大的 积分区间上采用低阶的Newton-Cotes公式进行计算,精度 又较低,为了提高求积的精度,常把积分区间分成若干相 等的子区间,在每个子区间上使用低阶公式,然后把结果 加起来,这样得到的求积公式叫做复化求积公式或复合求 积公式
由于高阶的Newton-Cotes公式不宜使用,而在比较大的 积分区间上采用低阶的Newton-Cotes公式进行计算,精度 又较低,为了提高求积的精度,常把积分区间分成若干相 等的子区间,在每个子区间上使用低阶公式,然后把结果 加起来,这样得到的求积公式叫做复化求积公式或复合求 积公式。 一、引言

二、复化梯形公式 将区间a,bl分成n等分,节点x=a+从,h=(b-a)/n,k=0,l,,n 对每一小区间[x,x] 采用梯形公式,然后相加,则得 I1=edk=e25v,+月 =9La)+o)+2空fax,月=7 (3.1 工称为复化梯形公式,下标n表示将区间n等分。若"(x)在 [a,]上连续,则它的误差为
二、复化梯形公式 将区间[a,b]分成n等分,节点 , ( )/ , 0,1, , k x a kh h b a n k n = + = − = 1 [ , ] k k x x 对每一小区间 + 采用梯形公式,然后相加,则得 1 1 1 1 0 0 ( ) ( ) [ ( ( ) ( ))] 2 k k n n b x k k a x k k h I f x dx f x dx f x f x + − − + = = = = + 1 1 [ ( ) ( ) 2 ( )] 2 n k n k h f a f b f x T − = = + + = (3.1) n T 称为复化梯形公式,下标n表示将区间n等分。若 f x ( ) 在 [ , ] a b 上连续,则它的误差为

EiU]=I-T= h2 (b-a)f"(n) 12台 12 (3.2) 类似地,若把区间2等分,并对每一小区间采用梯形公式, 然后加起来,记为T,则容易推得,T,与T有如下关系 (3.3) 其中 Hn=h∑f 为 Xk.XK+1 的中点,即=(+x (3.3)指出了计算In的递推关系,能在计算机上方便地实现
类似地, 若把区间2n等分, 并对每一小区间采用梯形公式, 然后加起来,记为 T2n , 则容易推得, T2n 与 Tn 有如下关系 1 2 0 [ ] ( ) ( ) ( ) 12 12 n T n n k k h h E f I T f b a f − = = − = = − − (3.2) 2 1 ( ) 2 T T H n n n = + (3.3) 其中 1 1 0 2 ( ) n n k k H h f x − + = = k k , 1 x x 1 + 2 k x + 为 1 1 2 1 ( ). 2 k k k x x x + + 的中点,即 = + (3.3)指出了计算T2n 的递推关系,能在计算机上方便地实现

三、复化Simpson公式 类似于复化梯形公式,可得 I-1a2/)*4.+8 (3.4 S称为复化Simpson公式,下标n表示将区间Ia,bln等分, 它的误差是 E/n=1-S.=-rasn≤b 2880 (3.5 容易验证Sn与Tn有如下关系: S,=T+ 3
三、 复化Simpson公式 类似于复化梯形公式,可得 ( ) 1 1 1 1 1 0 0 2 1 ( ) [ ( ) 4 ( ) ( )] 3.4 6 k k n n x k k n x k k k I f x dx f x f x f x S + − − + + = = = + + = n S 称为复化Simpson公式,下标n表示将区间[a,b] n等分, 它的误差是 4 (4) ( ) [ ] ( ). 2880 s n n b a E f I S h f a b − = − = − (3.5) 容易验证 Sn 与 Tn 有如下关系: 1 2 . 3 3 S T H n n n = +

又因为 从而可得 47n-工 4-1 (3.6) 例1分别用复化梯形公式和复化Simpson公式计算积分 cosxdx Jo e* 解积分的精确值为=-12.0703463164.TSn以及它们 的误差E,E 见表3.1
又因为 2 1 1 . 2 2 T T H n n n = + 从而可得 4 2 4 1 n n n T T S − = − (3.6) 例1 分别用复化梯形公式和复化Simpson公式计算积分 0 cos x I e xdx = 解 积分I的精确值为I=-12.0703463164 , n T n S 以及它们 的误差 , T s E E n n 见表3.1
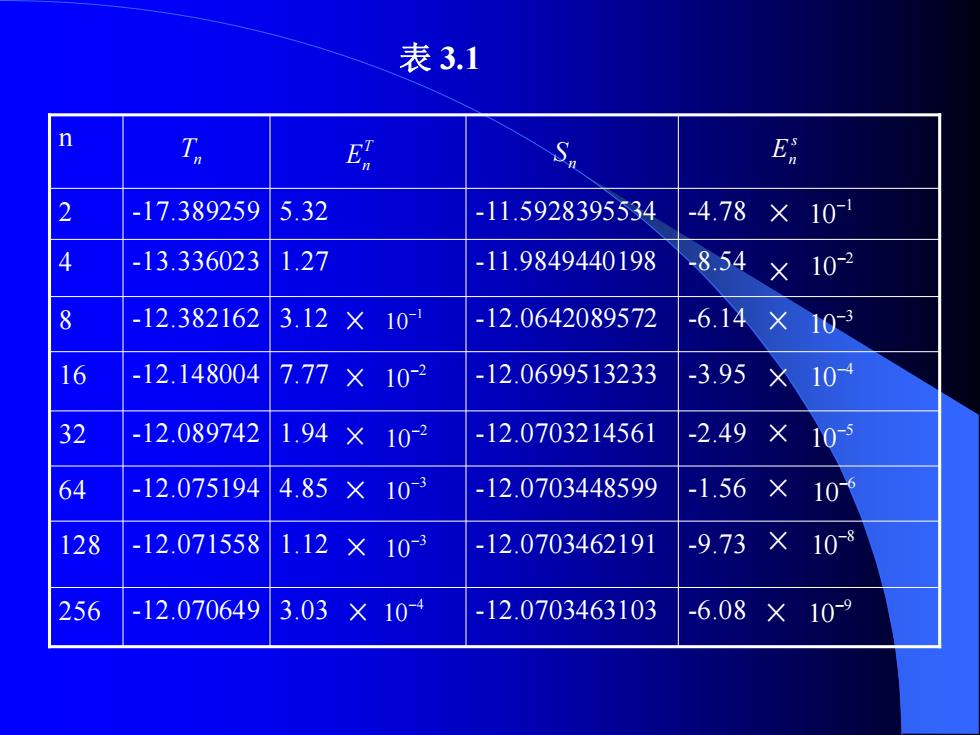
表3.1 n T E阳 S E 2 -17.389259 5.32 -11.5928395534 -4.78 ×10- 4 -13.336023 1.27 -11.9849440198 -8.54 ×102 8 -12.382162 3.12× 10- -12.0642089572 -6.14 10-3 16 -12.148004 7.77×102 -12.0699513233 -3.95 10 32 -12.089742 1.94×10-2 -12.0703214561 -2.49 ×10-3 64 -12.075194 4.85× 103 -12.0703448599 -1.56×109 128 -12.071558 1.12×10-3 -12.0703462191 -9.73×10-8 256 -12.070649 3.03×10 -12.0703463103 -6.08×109
-12.0703463103 -12.0703462191 -12.0703448599 -12.0703214561 -12.0699513233 -12.0642089572 -11.9849440198 -11.5928395534 -12.070649 -12.071558 -12.075194 -12.089742 -12.148004 -12.382162 -13.336023 1.27 -17.389259 5.32 256 128 64 32 16 8 4 2 表 3.1 Tn n T En n S s En -6.08 -9.73 -1.56 -2.49 -3.95 -6.14 -8.54 -4.78 1 10− 2 10− 3 10− 4 10− 5 10− 6 10− 8 10− 9 10− 3.03 1.12 4.85 1.94 7.77 3.12 2 10− 2 10− 1 10− 3 10− 4 10− 3 10−

复化Simpson公式比复化梯形公式精确得多,并随n的增 大,误差减少得很快。 例2若用复化梯形公式计算积分J,问积分区间要多少 等分才能保证使误差不超过×10? 解由估计式3.2)有 E[f]=- t-or--6" 12 12n2 其中f(x)=e,f"(x)=e,b-a=1,当0<x<1时有f"(x<e 从而 gV1sa
复化Simpson公式比复化梯形公式精确得多,并随n的增 大,误差减少得很快。 例2 若用复化梯形公式计算积分 1 0 x e dx ,问积分区间要多少 等分才能保证使误差不超过 1 4 10 2 − ? 解 由估计式(3.2)有 2 3 2 ( ) [ ] ( ) ( ) ( ) 12 12 T n h b a E f b a f f n − = − − = − 其中 f x e f x e b a ( ) , ( ) , 1, = = − = x x 当 0 1 x 时有 f x e ( ) , 2 12 T n e E f n 从而

若使近似积分的误差不超过,xl0,只需取n满足 e 2m≤2×10 或 16n2≥104e 两边取对数有 1g6+2lgn≥4+lge 整理得 1gn≥4+lge-lg6=18266 2 所以只要取=68,即将区间0,1]分68等分,就可使误差 1E,[/]s5×10
若使近似积分的误差不超过 1 4 10 2 − ,只需取n满足 4 2 1 10 12 2 e n − 或 2 4 16 10 n e 两边取对数有 lg6 2lg 4 lg + + n e 整理得 4 lg lg6 lg 1.8266. 2 e n + − = 所以只要取n=68,即将区间[0,1]分68等分,就可使误差 1 4 10 . 2 T E f n −

四、小结 1、引言 2、复化梯形公式 3、复化Simpson公式
四、小结 2、复化梯形公式 1、引言 3、 复化Simpson公式