
第一节Lagrange插值公式 一、插值问题的提法 二、线性插值 三、二次插值 四、n次插值 五、插值多项式的余项 六、小结
第一节 Lagrange插值公式 一、插值问题的提法 四、 n 次插值 二、线性插值 五、插值多项式的余项 六、小结 三、二次插值

插值问题的提法 在生产和科研中,经常会遇到这样的问题:由试验或观测得 到了某一函数关系y=f(x)在一系列点x,x,…,xn处的值 ,…,需要构造一个简单函数p(),使 y=f(x)≈p(x) 且满足条件y=9,(x),i=0,1,…n 这类函数逼近问题即为插值问题 o(x)称为f(x)的插值函数,x,称为插值节点, y,=p,(x),i=0,1,…n.称为插值条件
在生产和科研中,经常会遇到这样的问题:由试验或观测得 到了某一函数关系 在一系列点 处的值 ,需要构造一个简单函数 ,使 且满足条件 这类函数逼近问题即为插值问题. y = f (x) 0 1 , , , n x x x 0 1 , , n y y y ( x) y f x x = ( ) ( ) ( ), 0,1, . i i y x i n = = 一、插值问题的提法 称为 的插值函数, 称为插值节点, 称为插值条件. ( x) f (x) i x ( ), 0,1, . i i y x i n = =

设F(x)在n+1个不同点x处的函数值y(=1,2,;·m为已知, 要求构造一个次数不超过n的代数多项式 Pn(x)=4+ax+ax+…anx 使P(x)在节点处满足 P,()= i=1,2,…,n. (1.2) 这个问题称为n次代数插值问题。P,(x)称为(x)的插值函 数,x,称为插值节点,式Q.2)称为插值条件
设 F x( )在n +1个不同点xi处的函数值 ( 1,2,, ) Y I n i = L 为已知, 要求构造一个次数不超过 n的代数多项式 ( ) 2 0 1 2 n P x a a x a x a x n n = + + + (1.1) 使P x n ( )在节点 i x 处满足 P x y n i i ( ) = i n =1,2, , . (1.2) 这个问题称为 n次代数插值问题。 ( ) P x n 称为 F x( )的插值函 数,i x 称为插值节点,式(1.2)称为插值条件

可以证明,插值问题(1.1)(①2)的解是存在且唯一的。为了 得到Lagrange公式的一般形式,我们先从最简单的一次插 值入手。 二、线性插值 已知: Xo X V % 为 求一个一次多项式P(x),使满足 P(x)=yi=0,1 即求过点(x),(x)的一次曲线 y=R=X-王%+X-
可以证明,插值问题(1.1 1.2 )、( )的解是存在且唯一的。为了 得到 Lagrange 公式的一般形式,我们先从最简单的一次插 值入手。 x y 0 x 0 y 1 x 1 y 已知: 求一个一次多项式 1P x( ),使满足 1 ( ) , 0,1. P x y i i i = = 即求过点( x y x y 0 0 1 1 , , , ) ( )的一次曲线1 0 1 0 1 0 1 1 0 ( ) x x x x y P x y y x x x x − − = = + − − 二、线性插值

若记 ,)=X-五,4w=X0 X0一X1 x -Xo 则有 y=)+Hx)=∑y以,x) 显然 1,i=j 1,)=8=0.1≠j i,j=0,1
若记 1 0 0 1 0 1 1 0 ( ) , ( ) x x x x l x l x x x x x − − = = − − 则有 1 0 0 1 1 0 ( ) ( ) ( ) j j j y y l x y l x y l x = = + = 显然 1, ( ) 0, j i ij i j l x i j = = = i j , 0,1 =
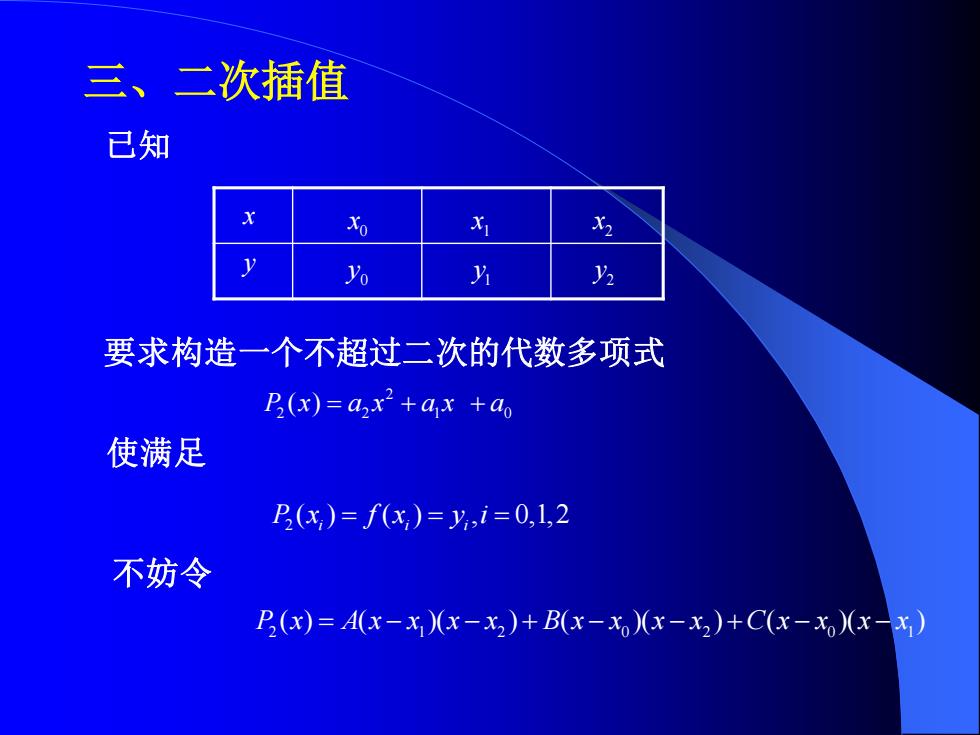
三、二次插值 已知 0 x X2 % 方 y2 要求构造一个不超过二次的代数多项式 B(x)=ax2+ax +ao 使满足 (x)=f(x,)=y,i=0,1,2 不妨令 B(x)=A(x-x)(x-x)+B(x-x)(x-x2)+C(x-x)(x-x)
三、二次插值 已知 x y 0 x 1 x 2 x 0 y 1 y 2 y 要求构造一个不超过二次的代数多项式 2 2 2 1 0 P x a x a x a ( ) = + + 使满足 2 ( ) ( ) , 0,1,2 P x f x y i i i i = = = 不妨令 2 1 2 0 2 0 1 P x A x x x x B x x x x C x x x x ( ) ( )( ) ( )( ) ( )( ) = − − + − − + − −

由条件(x,)= 0=01,2),得 A=%(x。-x)(x。-x2) B=/x)(x2) C=y2/(x2-xo)(x2-x) 于是得到二次插值(或抛物插值)函数 -2- ),(x-x)x-x2 (G-x3-)+ x-x)x-x2) ,(x-x)(x-x)》 (32-x)(2-x) (1.3) 若记 1) (x-x)x-x2) (x-x)(x0-x2) 4(x)= (x-x)(x-x2) 12(x)= (x-x)(x-x) x-x)(x-x) (x2-x)(x2-x)
由条件 2 ( ) ( 0,1,2) P x y i i i = = , 得 0 0 1 0 2 1 1 0 1 2 2 2 0 2 1 /( )( ) /( )( ) /( )( ) A y x x x x B y x x x x C y x x x x = − − = − − = − − 于是得到二次插值(或抛物插值)函数 ( )( ) ( )( ) ( )( ) ( )( ) ( )( ) ( )( ) 1 2 0 2 2 0 1 0 1 0 2 1 0 1 2 0 2 2 2 0 2 1 ( ) x x x x x x x x P x y y x x x x x x x x x x x x y x x x x − − − − = + − − − − − − + − − (1.3) ( )( ) ( )( ) 1 2 0 0 1 0 2 ( ) x x x x l x x x x x − − = − − ( )( ) ( )( ) 0 2 1 1 0 1 2 ( ) x x x x l x x x x x − − = − − ( )( ) ( )( ) 0 1 2 2 0 2 1 ( ) x x x x l x x x x x − − = − − 若记

或统一写成7,()=-j=0,12 则(1.3)成为 Bx)=,x)+4()+4()=∑x) 此式成为抛物插值的Lagrange形式。其中,(x)具有如下性质: 8- i≠》 i,j=0,12
或统一写成 2 0 ( ) , 0,1,2 i j i j i i j x x l x j = x x − = = − 则(1.3)成为 2 2 0 0 1 1 2 2 0 2 2 0 0 ( ) ( ) ( ) ( ) ( ) ( ) j j j i j j i j i i j P x y l x y l x y l x y l x x x y x x = = = = + + = − = − 此式成为抛物插值的 Lagrange 形式。其中 ( ) j l x 具有如下性质: 1, ( ) 0, j i ij i j l x i j = = = i j , 0,1,2 =

四、n次代数插值 已知 y 求作一个不超过n次的代数多项式P.(x)使满足 P(x)=f(x,),i=0,1,…n 不妨令 P(=∑y (14)
四、n次代数插值 已知 x y 0 x 0 y 1 x 1 y n y n x 求作一个不超过 n 次的代数多项式 ( ) P x n 使满足 ( ) ( ), 0,1, P x f x i n n i i = = 不妨令 ( ) ( ) 1 n n j j j P x l x y = = (1.4)

P()=,()y (1.4) 其中,1,(x)为n次多项式,称为插值基函数,它满足条件 ,(3)=⊙,= 1,i=j (1.5 0,i≠ 这样,问题(1.1)(12)转化为:在条件1.5)下,构造 个形如(1.4)的代数多项式。 依条件1.5),容易得到 1,(x)=A(x-x)(x-x)…(x-x-)(x-x#)…(x-xn) A=y,(x,-xx,-x)…(x,-x-x,-x)(x-xn)
( ) ( ) 1 n n j j j P x l x y = = (1.4) 其中,l x j ( )为 n 次多项式,称为插值基函数,它满足条件 ( ) 1, 0, j i ij i j l x i j = = = (1.5) 这样,问题(1.1 1.2 )、( )转化为:在条件(1.5) 下,构造一 个形如(1.4)的代数多项式。 依条件(1.5),容易得到 0 1 1 1 ( ) ( )( ) ( )( ) ( ) j j j n l x A x x x x x x x x x x = − − − − − − + 0 1 1 1 /( )( ) ( )( ) ( ) A y x x x x x x x x x x = − − − − − j j j j j j j j n − +