
第二节Euler方法 Euler方法 二 改进Euler方法 三、小结
第二节 Euler 方法 一 Euler 方法 三、小结 二 改进 Euler 方法

Euler方法 给定初值问题 y'=f(x,y) (1.1) y(x)= (1.2) 其中f(x,y)为x,y的已知函数,是给定的常数, 求(1.1)、(1.2)的数值解。 Eler方法是解初值问题(1.1)、(1.2)是简单 数值解法。由于它的精确度不高,实际计算中已 不被采用,然而它在苛种程度上却反映了数值解法 的基本思想
给定初值问题 其中 为 的已知函数, 是给定的常数, 求(1.1)、(1.2)的数值解。 f x y ( , ) x y, 0 y 一 Euler 方法 0 0 ( , ) ( ) y f x y y x y = = (1.1) (1.2) 方法是解初值问题(1.1)、(1.2)是简单 数值解法。由于它的精确度不高, 实际计算中已 不被采用,然而它在苛种程度上却反映了数值解法 的基本思想。 Euler
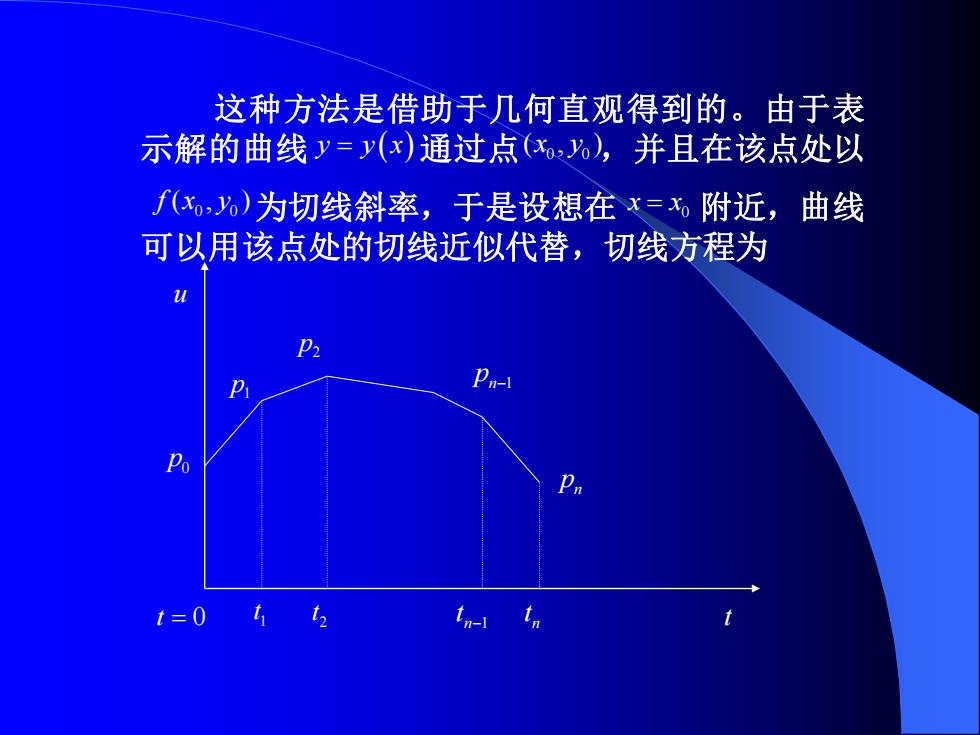
这种方法是借助于几何直观得到的。由于表 示解的曲线y=(x)通过点(x),并且在该点处以 (x,%)为切线斜率,于是设想在x=附近,曲线 可以用该点处的切线近似代替,切线方程为 u Pn- Po t=0 412 tn-1 In
0 p 1 p 2 p pn−1 n p t = 0 1 t 2 t n 1 t − n t u t 这种方法是借助于几何直观得到的。由于表 示解的曲线 通过点 ,并且在该点处以 为切线斜率,于是设想在 附近,曲线 可以用该点处的切线近似代替,切线方程为 0 0 ( , ) x y 0 0 f x y ( , ) 0 x x = y y x = ( )

y=yo +f(ao)(x-xo) 也就是说,x=x时,y=(x)可用+f(x,y)h近 似代替,记这个值为y,即 y=%+h时(x,%) 于是给出了一种当x=x时,获得函数值(x)的近 似值的方法。重复上面的作法,在x=x处,就 可以得到y(x2)的近似值 y2=y+hf(,)
0 0 0 0 y y f x y x x = + − ( , )( ) 也就是说, 时, 可用 近 似代替,记这个值为 ,即 1 x x = 1 y x = ( ) 0 0 0 y f x y h + ( , ) 1 y 1 0 0 0 y y hf x y = + ( , ) 于是给出了一种当 时,获得函数值 的近 似值 的方法。重复上面的作法,在 处,就 可以得到 的近似值 1 x x = 1 y x( ) 1 y 2 x x = 2 y x( ) 2 1 1 1 y y hf x y = + ( , )

依此下去,当y已经得到,则 ynt =yn+hf(nn) 这就是著名的Euler方法的计算格式。 由于uler方法是用一条折线近似地代替曲 线y(x),所以Eler方法也叫Eler折线法。 种计算格式,当在计算y时,仅仅用到 它前一步的信息y,称它为单步法。可见卫所法 就是单步法
1 ( , ) n n n n y y hf x y + = + 依此下去,当 yn 已经得到,则 这就是著名的 Euler 方法的计算格式。 Euler Euler 由于 方法是用一条折线近似地代替曲 线 y x( ) ,所以 Euler 方法也叫 折线法。 Euler n 1 y + n y 一种计算格式,当在计算 时,仅仅用到 它前一步的信息 ,称它为单步法。可见 方法 就是单步法

改进的Euler方法 将方程(1.1)在区间[x,x]上求积分,便得到 x)-)=∫fx,x》d (1.4) (1.4)式中右端的积分,可以用数值积分法计 算它的近似值。例如,使用矩形公式则有 y(x)≈+f(x,) 上式右端就是用Euler方法得到的y,即
将方程(1.1)在区间 x x 0 1 , 上求积分,便得到 (1.4)式中右端的积分,可以用数值积分法计 算它的近似值。例如,使用矩形公式则有 1 0 0 0 y x y hf x y ( ) ( , ) + 二 改进的 Euler 方法 1 0 1 0 ( ) ( ) ( , ( )) x x y x y x f x y x dx − = (1.4) 上式右端就是用 Euler 方法得到的 y1 ,即

乃=a+h时(x,%) 一般地有 y=yn+hf(xn,yn》 这就是Euler公式(1.3)。 由此可见,E访法出可以看成用矩形公式近 似计算某个相应的定积分而得到的。因此可以说, 方跑灾忾以精确度不高,正是由于它在计算定 积分时,采用矩形公式的缘故。 倘若使用较为精确的梯形公式来计算(1.4)式 中右端的积分,即
1 0 0 0 y y hf x y = + ( , ) 一般地有 1 ( , ) n n n n y y hf x y + = + 这就是 Euler 公式(1.3)。 由此可见, 方法出可以看成用矩形公式近 似计算某个相应的定积分而得到的。因此可以说, 方法也之忾以精确度不高,正是由于它在计算定 积分时,采用矩形公式的缘故。 Euler Euler 倘若使用较为精确的梯形公式来计算(1.4)式 中右端的积分,即

∫fx,x≈,L/,tfx川 )L/(x,%)+f(x⅓】 将它代入(1.4)式的右端,便得到(x)的近似值, 片=%+2/w)+fx+y】 用同样的方法可以得到2,,·。一般地有, =a+2f3y)+fya】 (1.5)
1 0 0 0 1 1 ( , ( )) [ ( , ) ( , ( ))] 2 x x h f x y x dx f x y f x y x + 将它代入(1.4)式的右端,便得到 y x( )1 的近似值 y1 , 1 0 0 0 1 1 [ ( , ) ( )] 2 h y y f x y f x y = + + + 用同样的方法可以得到 y y 2 3 , , 。一般地有, 0 0 1 1 [ ( , ) ( , )] 2 h + f x y f x y 1 1 1 [ ( , ) ( , )] 2 n n n n n n h y y f x y f x y + + + = + + (1.5)

这就是改进的Eler方法的计算格式。值 得注意的是Euler方法中yi是由已知的或已 经算出的量来表达的,得到期它不需要解方程, 这类方法通常称为显示方法;而在改进Ele访 法中,未知数y也隐含在方程右端之中, 对于每一个y的值都需要通过解方程才能 得到,这类方法通常称为隐式格式。在多数情 况下,要从隐式格式(1.5)中解出y+1是很困 难的。因此,通常采用如下的迭代方法来求解。 即先用Euler方法算出一个结果,作为(1.5)式 的初值,进行迭代,其计算格式为
n 1 y + n 1 y + n 1 y + n 1 y + 这就是改进的 方法的计算格式。值 得注意的是 方法中 是由已知的或已 经算出的量来表达的,得到期它不需要解方程, 这类方法通常称为显示方法;而在改进 方 法中,未知数 也隐含在方程右端之中, 对于每一个 的值都需要通过解方程才能 得到,这类方法通常称为隐式格式。在多数情 况下,要从隐式格式(1.5)中解出 是很困 难的。因此,通常采用如下的迭代方法来求解。 即先用 方法算出一个结果,作为(1.5)式 的初值,进行迭代,其计算格式为 Euler Euler Euler Euler

9=,+,》 (1.6) =+与1frn】 (k=01,2…) 由 "-周-=r0xw-f4) 可知,当L<1时,迭代格式收敛。也就是说, 只要取得充分小,就可能保证迭代序列
(0) 1 ( 1) ( ) 1 1 1 ( , ) [ ( , ) ( , )] ( 0,1, 2 ) 2 n n n n k k n n n n n n y y hf x y h y y f x y f x y k + + + + + = + = + + = (1.6) ( 1) ( ) ( ) ( 1) 1 1 1 1 1 1 ( , ) ( , ) 2 k k k k n n n n n n h y y f x y f x y + − + + + + + + − = − 由 ( ) ( 1) 1 1 2 k k n n h L y y − − + + 可知,当 时,迭代格式收敛。也就是说, 只要 取得充分小,就可能保证迭代序列 1 2 h L h