§6.3一阶线性微分方程 主要内容 一阶齐次线性 阶非齐次线性 微分方程 微分方程
§6.3 一阶线性微分方程 主要内容 一阶齐次线性 微分方程 一阶非齐次线性 微分方程
一阶线性微分方程的定义 定义1:形如 +P代y-的方程叫徽一阶线性微分方程其中 P(x),Q(x) 只含未知函数的 未知函数是一次 为已知函数 一阶导数且系数 的 为1 Q(x)≠0 Q(x)=0 称为非齐次 d+P(x)y=Q(x) 称为齐次 线性方程 d 线性方程 已知函数 已知函数 方程 +Px)y=0叫做对应于非齐次线性方程 dx +P(x)y=Qx)的齐次线性方程
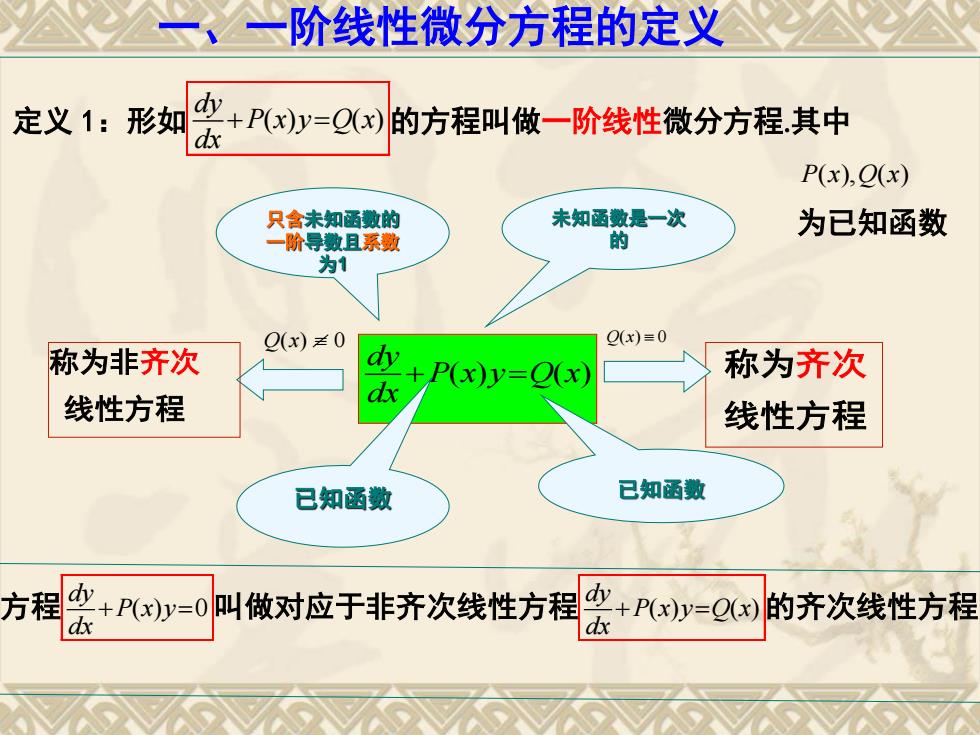
定义 1:形如 P(x)y Q(x) dx dy 的方程叫做一阶线性微分方程其中 P(x)y Q(x) dx dy 已知函数 已知函数 未知函数是一次 的 只含未知函数的 一阶导数且系数 为1 称为齐次 线性方程 方程 P(x)y0 dx dy 叫做对应于非齐次线性方程 P(x)y Q(x) dx dy 的齐次线性方程 一、一阶线性微分方程的定义 Q x( ) 0 称为非齐次 线性方程 Q x( ) 0 P x Q x ( ), ( ) 为已知函数

一阶线性微分方程的定义 课堂训练1:判断正误:下列错误的是 d d +P(x)y=Q(x) (1) 少-y=1是一阶线性微分方程. d (2) y少-ry=simx是一阶线性微分方程, dx (3) 少-2少=0是一阶齐次线性微分方程。 dx x+1 (4) 少-2义=(:+1)是一阶非齐次线性微分方程 dx x+1
课堂训练 1:判断正误:下列错误的是 (1) 1 2 y dx dy 是一阶线性微分方程 (2) 2 sin dy y x y x dx 是一阶线性微分方程 P(x)y Q(x) dx dy 一、一阶线性微分方程的定义 (3) 2 0 1 dy y dx x 是一阶齐次线性微分方程 (4) 5 2 2 1 1 dy y x dx x 是一阶非齐次线性微分方程
、一阶非线性微分方程的解法一常数变易法 +Py=0(1)的解法 (2)的解法 dx +Pwy=O(x d 第一步分离变量 第四步设通解 dy y=ux)e --P(x)dx y 第五步代入求出u(x) 第二步两边积分 u(x)=Q(x)e Inly-∫P(x)+C 第六步代入求出u(x) x)=∫Ox)er dx+C 第三步求出通解 第七步代入求出y y=CePx(C=±eS) y-SO(
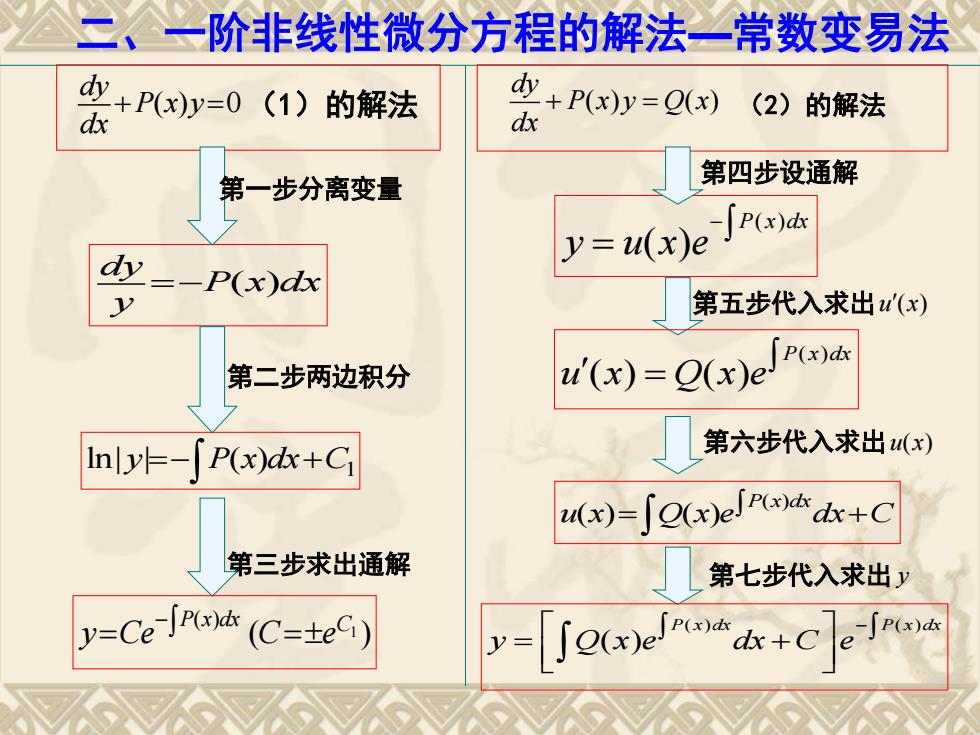
P(x)y0 dx dy (1)的解法 ( ) ( ) dy P x y Q x dx (2)的解法 二、一阶非线性微分方程的解法—常数变易法 P x dx y dy ( ) 第一步分离变量 第二步两边积分 1 ln| y| P(x)dxC 第三步求出通解 ( ) 1 P(x)dx C y Ce Ce ( ) ( ) P x dx y u x e 第四步设通解 第五步代入求出 u x ( ) ( ) ( ) ( ) P x dx u x Q x e 第六步代入求出 u x( ) u x Q x e dx C P x dx ( ) ( ) ( ) 第七步代入求出 y ( ) ( ) ( ) P x dx P x dx y Q x e dx C e

二、一阶非线性微分方程的解法一常数变易法 例求方程 少 2y=(+)2的通解 dx x+1 y=u(x+1)2 dy 2y 解: 先求x+1 0的通解。 (5)把y代入所给非齐次线性方程,得 2'=(x+1)2 (1) dy2dx 分离变量得yx+1 (6)两边积分,得 (2)积分得lny=2lnx+1+C 3 u= 3(x+1)2+C (3)即齐次线性方程的通解为 (7)将山代入得方程的通解为 y=C(x+1)2 2 (4)常数变易:把C换成u, y=x+3+C(+I
二、一阶非线性微分方程的解法—常数变易法 例 求方程 2 5 ( 1) 1 2 x x y dx dy 的通解 解: 先求 0 1 2 x y dx dy 的通解 (1)分离变量得 1 2 x dx y dy (2)积分得 1 ln 2ln 1 y x C (3)即齐次线性方程的通解为 2 y C x 1 (4)常数变易:把C 换成u 2 y u x 1 (5)把 y 代入所给非齐次线性方程 得 1 2 u x ( 1) (6)两边积分,得 3 2 2 ( 1) 3 u x C (7)将u 代入得方程的通解为 7 2 2 2 ( 1) ( 1) 3 y x C x