
高等数学(上册) 同济版少课时课件 南阳师范学院-数学与统计学院 王阳
高 等 数 学 (上册) ----同济版少课时课件 南阳师范学院--数学与统计学院 数学与统计学院 王 阳

引言 一、什么是高等数学? 初等数学 高等数学 以静止的观点 以运动的观点 研究常量 研究变量及其依赖关系
一、什么是高等数学? 引 言 初等数学 以静止的观点 研究常量 高等数学 以运动的观点 研究变量及其依赖关系

引言 二、高等数学的主要内容 1.基础: (1)函数(2)极限(3)连续 2.微积分学:一元微积分、多元微积分 3.向量代数与空间解析几何 4.无穷级数 5.常微分方程
引 言 二、高等数学的主要内容 1. 基础: (1)函数 (2)极限 (3)连续 2. 微积分学: 3. 向量代数与空间解析几何 4. 无穷级数 5. 常微分方程 一元微积分、 多元微积分

引言 三、本学期的教学内容 第一章函数与极限 第二章导数与微分 第三章, 中值定理与导数的应用 第四章 不定积分 第五章 定积分及其应用
第一章 函数与极限 第二章 导数与微分 第三章 中值定理与导数的应用 第四章 不定积分 第五章 定积分及其应用 三、本学期的教学内容 引 言

引言 四、学习高等数学的基本要求 1.预--课前预习(提前5分钟交预习问题) 2.听听课(点名) 3.记--做笔记;复习 4.练--训练:作业-练习题-自测题 ormal
1. 预------课前预习(提前5分钟交预习问题) 2. 听------听课(点名) 3. 记------做笔记;复习 4. 练------训练:作业--练习题--自测题 引 言 四、学习高等数学的基本要求

引言 五、考试形式 1.平时成绩(20)+期末卷面成绩(80) 2.平时成绩-点名+作业+课堂表现+预习 3.期末考试--形式:闭卷(100分) 题型:判断题;填空题;单项选择题;计算题;证明题
1. 平时成绩(20)+期末卷面成绩(80) 2. 平时成绩-----点名+作业+课堂表现+预习 3. 期末考试------形式:闭卷(100分) 题型:判断题;填空题;单项选择题;计算题;证明题 引 言 五、考试形式

第一章i 函数与极限 主要内容 一、数列的极限 二、函数的极限 三、无穷大、无穷小及无穷小的比较 四、极限存在准则及两个重要极限 五、函数的连续性
第一章 函数与极限 主要内容 一、数列的极限 二 、函数的极限 三、无穷大、无穷小及无穷小的比较 四、极限存在准则及两个重要极限 五、函数的连续性

§1.1 :函数 主要内容: 集合 有界性 有关的概念 区 间 函数 函数的 单调性 奇偶性 反函数 复合函数 特性 周期性 初等函数
§1.1 函数 主要内容: 有 关 的 概 念 集 合 区 间 函 数 反函数 复合函数 初等函数 函 数 的 特 性 有界性 单调性 奇偶性 周期性

一、集合与区间 1.与集合有关的概念 2.集合的表示法与运算 (1)我们把具有某种特定性质的事物的总体K1)列举法:把集合的全体元素 称为一个集合,用A,B,M等表示. 一一列举出来 (2)组成集合的事物称为集合的元素. 自然数集N=0,1,2,n, 事物a是集合M的元素表示为aeM 正整数集Nt={1,2,,n, 事物a不是集合M的元素表示为a生Mz--n,-2,-1,0,1,2,n} (3)由有限个元素组成的集合称为有限集, (2)描述法:M=x|x具有性质P) 由无限个元素组成的集合称为无限集. 实数集R={x为有理数或无理数) 不含任何元素的集合称为空集,记作②. (4)若集合A的元素都是集合B的元素,则 AUB-{xx∈A或x∈B. 称A是B的子集.记作AB或A. AnB-(xx∈A且x∈B}. (5)若集合A与集合B互为子集,则称A与B AB-{xx∈A且xEB. 相等.记作A=B
一、集合与区间 1. 与集合有关的概念 2.集合的表示法与运算 (1)我们把具有某种特定性质的事物的总体 称为一个集合. 用A, B, M 等表示. (2)组成集合的事物称为集合的元素. 事物 a 是集合 M 的元素表示为 a∈ M . 事物 a 不是集合 M 的元素表示为a∉M (3)由有限个元素组成的集合称为有限集 . 由无限个元素组成的集合称为无限集 . 不含任何元素的集合称为空集,记作∅. (4)若集合A的元素都是集合B的元素,则 称A是B的子集.记作A⊂B或B⊃A . (5)若集合A与集合B互为子集,则称A与B 相等.记作A=B (1)列举法: 把集合的全体元素 一一列举出来. 自然数集 N={0, 1, 2, {0, 1, 2, ⋅ ⋅ ⋅, n, ⋅ ⋅ ⋅}. 正整数集 N+={ 1, 2, { 1, 2, ⋅ ⋅ ⋅, n, ⋅ ⋅ ⋅}. Z={⋅ ⋅ ⋅, −n, ⋅ ⋅ ⋅, −2, −1, 0, 1, 2, 1, 0, 1, 2, ⋅ ⋅ ⋅, n, ⋅ ⋅ ⋅} (2)描述法:M={x | x 具有性质 P }. 实数集R xx = { 为有理数或无理数} A∪B={x|x∈A或x∈B}. A∩B={x|x∈A且x∈B}. A\B={x|x∈A且x∉B}
一、集合与区间 3.区间 4.邻域 (1)开区间: (a,b)={xa<r<b}. (1)点a的6邻域:Ua,可=xl川x-aK列 (2)闭区间: [a,b={xla≤≤b} (2)去心邻域:0(a,可=0<x-ak6 (3)半开区间:a,b)=x|s<} 注记2:Ua,-(a-6,a+6) (a,b=x|a<≤b} (4)无穷区间:【a,+o)=|心x} 注记3:U(a,=(a-6,a)U(a,a+d) (-o,b1=x|x≤b} (a,+o)=c|b<x} (-o,b,)={xlx<b} 注记1:实数集R=(-0,+),其中-0,+o只是 表示无限性的一种记号,它们不是某个确定的数
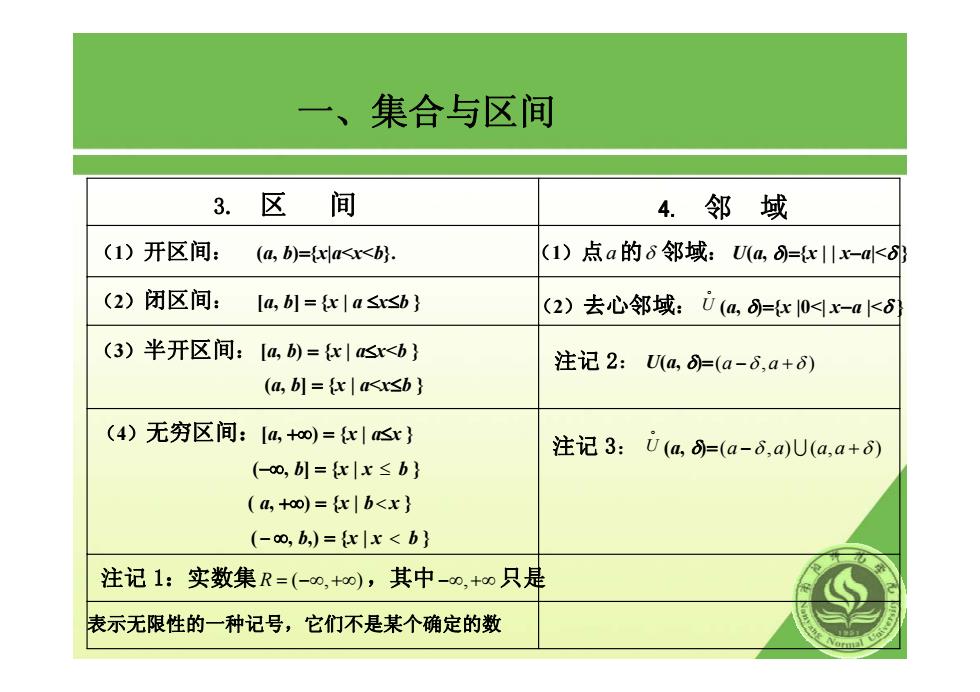
一、集合与区间 3. 区 间 4. 邻 域 (1)开区间: (a, b)={x|a<x<b}. (2)闭区间: [a, b] = {x | a ≤x≤b } (3)半开区间: [a, b) = {x | a≤x<b } (a, b] = {x | a<x≤b } (4)无穷区间:[a, +∞) = {x | a≤x } (−∞, b] = {x | x ≤ b } ( a, +∞) = {x | b< x } ( − ∞, b,) = {x | x < b } 注记 1:实数集R = −∞ +∞ (,),其中−∞ +∞ , 只是 表示无限性的一种记号,它们不是某个确定的数 (1)点a的δ 邻域: U(a, δ)={x | | x−a|<δ } (2)去心邻域: D U (a, δ)={x |0<| x−a |<δ } 注记 2: U(a, δ)=(, ) a a −δ +δ 注记 3: D U (a, δ)=( ,) (, ) a a aa −δ ∪ + δ