
第二节Gauss--Seidel迭代法 一、 Gass--Seidel迭代格式 二Gauss--Seideli迭代法的收敛性 三、小结
第二节 Gauss Seidel − − 迭代法 一、 Gauss Seidel − − 迭代格式 二 Gauss Seidel − − 迭代法的收敛性 三、小结

一、 Gauss--Seidel迭代格式 考虑方程组 x1=bx+b2x2+…+bnxn+f x2=b2x1+b2x2+…+b2nxn+2, xn=bnx1+…十bnm-xn-1+bmxn+fn 即 -立x+1=2m (2.1)
一、 Gauss Seidel − − 迭代格式 1 11 1 12 2 1 1 2 21 1 22 2 2 2 1 1 1 1 , , . n n n n n n nn n nn n n x b x b x b x f x b x b x b x f x b x b x b x f − − = + + + + = + + + + = + + + + 考虑方程组 1 , 1, 2, , n i ij j i j x b x f i n = = + = (2.1) 即

对方程组(2.1)作迭代时,取定初始近似值 x,x9,…x0 以后,把它们代入(2.1)中第一个方程算出 =b+b2x2+bnx+ 显然,迭代格式收敛的话,则x0比x更接近于 X的第一个分量x所以在计算x时,我们不再像acobi 迭代法那样以x,x9,x9代入(2.1)中第二式的右边 而是把新算出的x”及x,x°,x°代入该式右边,得 到 x0=么x0+bnx0+-bx0+万
以后,把它们代入(2.1)中第一个方程算出 (1) (0) (0) (0) 1 11 1 12 2 1 1 n n x b x b x b x f = + + + + (0 0 0 ) ( ) ( ) 1 2 , , n x x x 对方程组(2.1)作迭代时,取定初始近似值 X 显然,迭代格式收敛的话,则 比 更接近于 的第一个分量 所以在计算 时,我们不再像 迭代法那样以 代入(2.1)中第二式的右边 , 而是把新算出的 及 代入该式右边,得 到 (1) 1 x (0) 1 x * 1 x (1) 2 x Jacobi (0 0 0 ) ( ) ( ) 1 2 , , n x x x (1) 1 x (0 0 0 ) ( ) ( ) 2 3 , , n x x x (1) (1) (0) (0) 2 21 1 22 2 2 2 n n x b x b x b x f = + + +

即计算下一个分量时,要用到刚算出的新 分量。这样或许能收到更好的效果。按这 样方式建立的迭代格式称为Gauss--Seidel 迭代格式,其一般形式为 x=么x+4x++x,+ w=,x+b2x++bx,+ (2.2 x=bx++b-+bx0+/
即计算下一个分量时,要用到刚算出的新 分量。这样或许能收到更好的效果。按这 样方式建立的迭代格式称为 迭代格式,其一般形式为 Gauss Seidel − − ( 1) ( ) ( ) ( ) 1 11 1 12 2 1 1 ( 1) ( 1) ( ) ( ) 2 21 1 22 2 2 2 ( 1) ( 1) ( 1) ( ) 1 1 1 1 , , . k k k k n n k k k k n n k k k k n n nn n nn n n x b x b x b x f x b x b x b x f x b x b x b x f + + + + + + − − = + + + + = + + + + = + + + + (2.2)
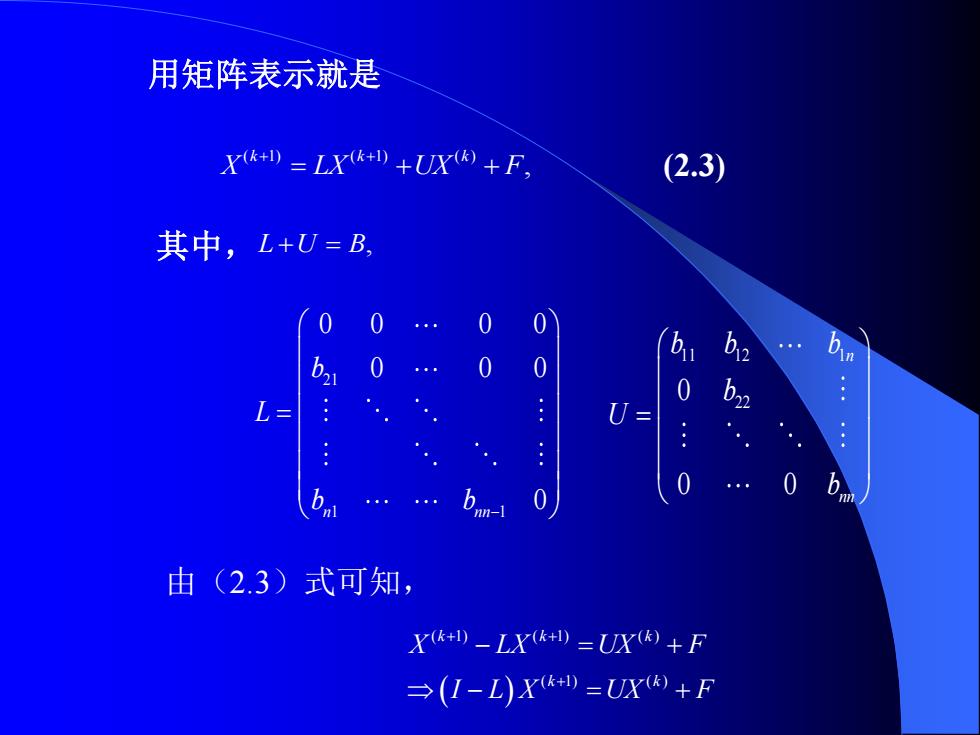
用矩阵表示就是 X(k+1)=LX(k+)tux(k)+F (2.3) 其中,L+U=B, 0 0 0 0 0 0 0 0 L= .: : U= 0 0 0 0 由(2.3)式可知, X(k+)-LX(k+)=UX(k)+F 三(I-Z))X+=X+F
用矩阵表示就是 ( 1) ( 1) ( ) , k k k X LX UX F + + = + + (2.3) 其中, L U B + = , 11 12 1 22 0 0 0 n nn b b b b U b = 21 1 1 0 0 0 0 0 0 0 0 n nn b L b b − = 由(2.3)式可知, ( ) ( 1) ( 1) ( ) ( 1) ( ) k k k k k X LX UX F I L X UX F + + + − = + − = +

因(1-L)存在,所以迭代格式(2.3) 也可表示为 X(+D)=(I-L)UX(k)+(I-L)F (2.4) 我们称G=(I-L)U为Gauss--Seidel 迭代法的迭代矩阵。 由(2.4)式可见,对方程组 X=BX+F作 Gass--Seidel迭代,等价于对方程组 X=(I-LUX+(I-L)F (2.5) 作Jacobi迭代
因 存在,所以迭代格式(2.3) 也可表示为 ( ) 1 I L − − ( 1) 1 ( ) 1 ( ) ( ) k k X I L UX I L F + − − = − + − (2.4) 我们称 为 迭代法的迭代矩阵。 ( ) 1 G I L U− = − Gauss Seidel − − 由(2.4)式 可见,对方 程 组 作 迭代,等价于对方程组 X BX F = + Gauss Seidel − − 1 1 X I L UX I L F ( ) ( ) − − = − + − (2.5) 作 Jacobi 迭代

二Gauss--Seidel:迭代法的收敛性 由于对方程组 X=BX+F 作Gass--Seidel迭代同对方程组 X=(I-L)UX+(I-L)F 作简单迭代是一回事,故由定理1有 定理3 对于任意右端向量和初始向量x Gauss---Seidel迭代法收敛的充要条件是 p(G)<1, 其中G=(1-LU
二 Gauss Seidel − − 迭代法的收敛性 定理 3 对于任意右端向量和初始向量 , 迭代法收敛的充要条件是 (0) X Gauss Seidel − − ( ) 1, G 其中 1 G I L U ( )− = − X BX F = + 由于对方程组 作简单迭代是一回事,故由定理1有 作 Gauss Seidel − − 迭代同对方程组 1 1 X I L UX I L F ( ) ( ) − − = − + −

即特征方程 1-Z)'U-1=0 的根的绝对值小于1。 由于 I-L)U-1=-)0-I-L) 而 (7-L≠0
即特征方程 1 ( ) 0 I L U I − − − = 的根的绝对值小于1。 而 1 ( ) 0, I L − − 1 1 ( ) ( ) ( ) I L U I I L U I L − − − − = − − − 由于

所以在实际问题中,只需求出方程 1U-(1-L=0 (2.6 的根。 类似于定理2,我们还可以给出如下收敛的充分条件。 定理4. 对于任意右端向量F初始向量x Gauss---Seidel迭代法收敛的充分条件是 (0IB风=ma2b,水k (2)IL=max∑b,kl
类似于定理2,我们还可以给出如下收敛的充分条件。 ( ) 1 1 1 max 1; n ij j i B b = = ( ) 1 2 max 1. n ij i j B b = = U I L − − = ( ) 0 (2.6) 所以在实际问题中,只需求出方程 的根。 定理4 对 于 任 意 右 端 向 量 初 始 向量 , 迭代法收敛的充分条件是 F Gauss Seidel − − (0) X

由此定理可知,条件1)或(2)被满足时,则 Gauss--Seidel迭代法与Jacobi 迭代法都收敛。 可以证明,当条件(2)被满足时,Gauss---Seidel 迭代法比Jacobi迭代法收敛得快些。 例4分别用Jacobi 和Gauss--Seidel 迭代法解方程组 0.1 0.2\x 0.72 0.1 0 0.2 0.83 0.2 0.2 0.84
由此定理可知,条件(1)或(2)被满足时,则 Gauss Seidel − − 迭代法与 Jacobi 迭代法都收敛。 可以证明,当条件(2)被满足时, 迭代法比 Jacobi 迭代法收敛得快些。 Gauss Seidel − − 例4 分别用 和 迭代法解方程组 Jacobi Gauss Seidel − − 1 1 2 2 3 3 0 0.1 0.2 0.72 0.1 0 0.2 0.83 0.2 0.2 0 0.84 x x x x x x = +