第七章向量代数与空间解析几何 向量及有关概念 向量代数 向量的线性运算 数量积向量积及混合积 空间直角坐标系 空问解 平面与空间直线 析几何 旋转曲面与二次曲面
向量及有关概念 向量代数 向量的线性运算 数量积向量积及混合积 空间直角坐标系 空间解 析几何 平面与空间直线 旋转曲面与二次曲面 第七章 向量代数与空间解析几何
§7.1向量及其线性运算 主要 内容 向量及有 向量的加 关的概念 减法 数乘向量
主 要 内 容 数乘向量 向量及有 关的概念 向量的加 减法 §7.1 向量及其线性运算
一、向量及与向量有关的概念 向量的模 单位向量 零向量 两相等向 两向量 量 向量的 垂直 两互为反向 定义及表示 向量共面 量 两向量的夹 角 两向量平行
一、向量及与向量有关的概念 向量的模 单位向量 零 向 量 向量的 定义及表示 两向量的夹 角 两向量平行 两相等向 量 两互为反向 量 两向量 垂直 向量共面

二、向量的加减法 1.向量的加法(三角性法则) 2.向量的减法 设已知向量ā,b,以空间任意一点 规定两个向量的a与6的差 A为始点,连接作AB=ā,BC=b, a-b=a+(-b) c-a+b 由两向量a与6求它们差a-b的. 运算叫作向量的减法 B 连接AC,那么向量AC=c称为向量 a与b的和,记作c=a+b.由两向量 对任意的三点AB,C均有 a与b求它们和a+b的运算叫作向 AC=AB+BC,AC-AB=BC 量的加法
二、向量的加减法 1. 向量的加法(三角性法则) 2. 向量的减法 设已知向量 a, b ,以空间任意一点 A 为始点,连接作 AB a , BC b , a A B C b c a b 连接 AC ,那么向量 AC c 称为向量 a 与 b 的和,记作 c a b .由两向量 a 与b 求它们和 a b 的运算叫作向 量的加法. 规定两个向量的a与b 的差 a b a b ( ) 由两向量a 与b 求它们差a b 的. 运算叫作向量的减法. 对任意的三点 A,B,C 均有 AC AB BC , AC AB BC

二、向量的加减法 3.平行四边形法则 4.向量加法的运算法则 当向量ā与b不共线时,在空间中 对于任意的向量a,b我们有 任意取一点A,作AB=a,AD=b (1)a+0=a a+(-a列)=0 D a+h (2)交换律a+b=b+a B (3)结合律a+)+c=a+6+c) 以AB、AD为邻边作一平行四边形, ABCD,那么对角线向量 注记3:向量a,b,a+b,a-b共面 AC=AB+AD=a+b la-≤a+≤a+ DB=AB-AD=a-6
二、向量的加减法 3. 平行四边形法则 4. 向量加法的运算法则 当向量 a 与b 不共线时, 在空间中 任意取一点 A ,作 AB a AD b , A B D C a b a b 以 AB、 AD为邻边作一平行四边形, ABCD,那么对角线向量 AC AB AD a b DB AB AD a b 对于任意的向量a, b 我们有 (1) a a 0 ( ) 0 a a (2)交换律 a b b a (3)结合律a b c a b c 注记 3:向量a b a b a b , , , 共面 a b a b a b
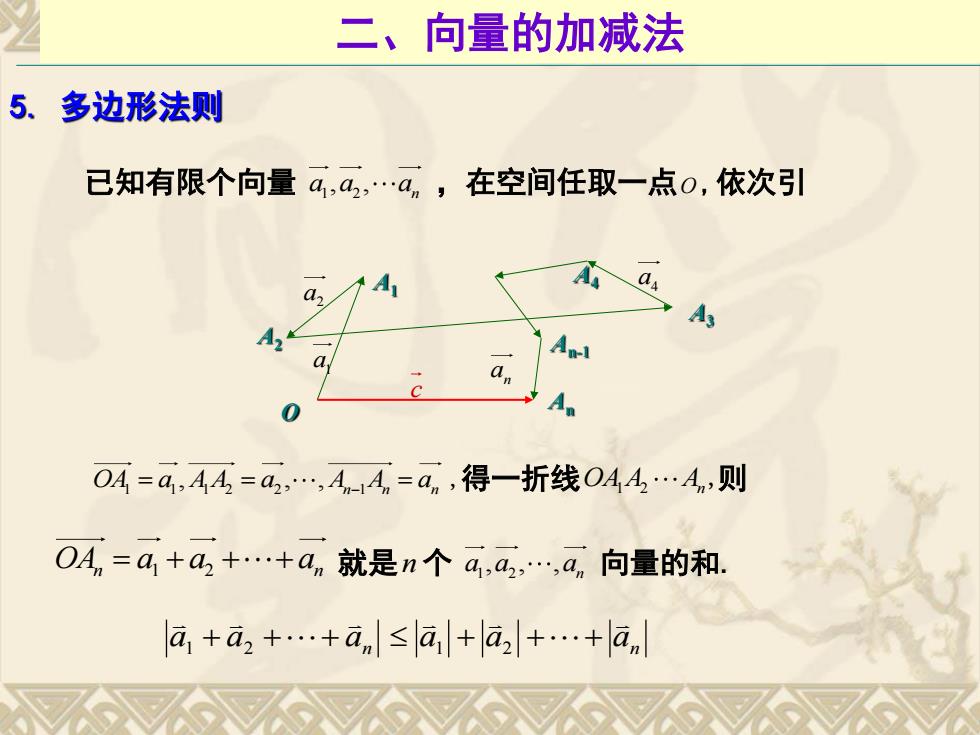
二、向量的加减法 5. 多边形法则 已知有限个向量a,a,…a,,在空间任取一点0,依次引 0A=a,44=4,…,4,-14,=a,得一折线044…An,则 OAn=a+a2+…+an就是n个a,a,…,an向量的和. a1+a2+…+an≤a+a2+…+an
A1 A2 A3 A4 An-1 1 a 4 a 2 a n a c 已知有限个向量 1 2 , , n a a a ,在空间任取一点O ,依次引 1 1 1 2 2 1 , , , OA a A A a A A a n n n , 得一折线OA A A 1 2 n , 则 就是n 个 1 2 , , , n OA a a a n n 1 2 a a a 向量的和. 5. 多边形法则 O An 二、向量的加减法 a a an 1 2 a a an 1 2

三、向量与数的乘法 1.数乘:实数1与向量ā的乘积是一个向量,记作1a, (1)模=2a; (2)2a的方向:1>0时,与a同向; 入<0时,与ā相反. 几=0时, 2ā=0,方向任意, 我们把这种运算叫做数量乘向量,简称数乘, 注记4:与非零向量ā同方向的单位向量。园
(1)模 a = a ; (2) a 的方向: 0时,与a 同向; 0时, 与a 相反. 我们把这种运算叫做数量乘向量,简称数乘. 1.数乘: 实数 与向量 a 的乘积是一个向量,记 作 a , 三、向量与数的乘法 0时, 0 a ,方向任意, 注记 4:与非零向量 a 同方向的单位向量 a a e a

三、向量与数的乘法 2. 数乘的运算规律 对于任意的实数2,u和任意的向量ā,b我们有 (1)1a=a,(-1)a=-d (2)关于数因子的结合律(ua)=()a (3)第一分配率(+)a=2ā+a (4)第二分配率(ā+b)=1ā+5
2. 数乘的运算规律 对于任意的实数, 和任意的向量 a , b 我们有 (1) a a 1 ,( 1) a a (2)关于数因子的结合律 ( ) ( ) a a (3)第一分配率 a a a ( ) (4)第二分配率 a b a b ( ) 三、向量与数的乘法

三、向量与数的乘法 定理1:向量b与非零向量ā平行的充要条件是存在唯一的实数2 使b=a. 注记5:设点0及单位向量确定的数轴为Ox轴,那么对于 数轴上的任意一点P,则存在唯一的实数x,使得 OP=xi 点P分向量OP实数x 因此定义实数x为数轴上点P的坐标, 由此可得数轴上点P的坐标为x的充要条件是OP=xi
定理 1:向量b 与非零向量 a 平行的充要条件是存在唯一的实数 使b a . 三、向量与数的乘法 注记 5: 设点O及单位向量i 确定的数轴为Ox 轴,那么对于 数轴上的任意一点P ,则存在唯一的实数x,使得 OP xi 点P 向量OP 实数x 因此定义实数 x 为数轴上点 P 的坐标. 由此可得数轴上点 P 的坐标为 x 的充要条件是OP xi

四、课堂训练 (1)若AB=a+5b,BC=-2a+86,CD=3a-36,则下列说法错误的是 (A)AD与AB共线 (B) D与B反方向 (C) A,B,D三点共线 (D) AD=26 (2)若M,N分别是△4BC边AB,AC的中点,则MN= BC (B) 1-2 (C)1 (D)-1 (3)在平行四边形ABCD中,下列说法不一定正确的是 (A) AD与BC是相等的向量 (B) AB与CD是互为反向量 (C) AD与BC的夹角为0 (D)AB 与cD夹角为π (E) AD BC,AB CD (F)AB与CD垂直
(1)若 AB a b BC a b CD a b 5 , 2 8 , 3 3 ,则下列说法错误的是 (A) AD 与 AB 共线 (B) AD 与 AB 反方向 (C) A B D , , 三点共线 (D) AD 2 AB 四、课堂训练 (2)(2)若M N, 分别是ABC边 AB AC , 的中点,则 MN BC (A)- 1 2 (B) 1 2 (C)1 (D)-1 (2)(3)在平行四边形 ABCD中,下列说法不一定正确的是 (A) AD 与 BC 是相等的向量 (B) AB 与 CD 是互为反向量 (C) AD 与 BC 的夹角为 0 (D) AB 与CD夹角为 (E) AD BC , AB CD (F) AB 与CD垂直