南阳师范学院：《高等数学》课程教学资源（课件讲稿）10.1 常数项级数的概念及性质

§10.1常数项级数的概念及性质 常数项级数概念 无穷级数性质 级数收敛的条件 应 用

§10.1 常数项级数的概念及性质 常数项级数概念 无穷 级数性质 级数 收敛的条件 应 用

回顾数列的性质 数列： 141,42,…,n,… 前n项和： Sn=4+山2+43，+…十un lim s=s n-→0 单调有界数列必收敛 若一数列收敛于5，则其任意的子列必收敛于s 若limS2n=S,limS2m1=S 若limS2n=S,limS2m1=S2,且 n→0 n-y0 1300 则 lims=s S1≠S2 则数列3，必发散 1→00

背景：求曲顶柱体的体积 一、 回顾数列的性质 数列： 1 2 , , , , n u u u   前 n 项和： 1 2 3, n n s u u u u     单调有界数列必收敛 若一数列收敛于s, 则其任意的子列必收敛于s 若 2 2 1 lim ,lim n n n n s s s s      若 2 1 2 1 2 lim ,lim n n n n s s s s      ，且 1 2 s s  则数列 n s 必发散 lim n n s s   则 lim n n s s  

二、常数项级数的概念 设有数列 4,，把它的项依次用加号连起来，所得的式子 即 un 41+42+%3…+,+ 记为吃4 称为常数项级数. 第n项n叫做级数的一般项 级数的前n项和Sn=4+山2+43+…+山n称为级数的部分和 S,52,S,…称为部分和数列，记作{Sn} 00 如果级数 山，的部分和数列 则称无穷级数 4n收敛，这时极限 n=] n= Sn 有极限s(有限)即lim s=s n→0 ,叫做这级数的和，并写成5=∑4 n=l 如果级数 u.的部分和数列 则称级数 n=l ∑，发散 2= Sn不存在

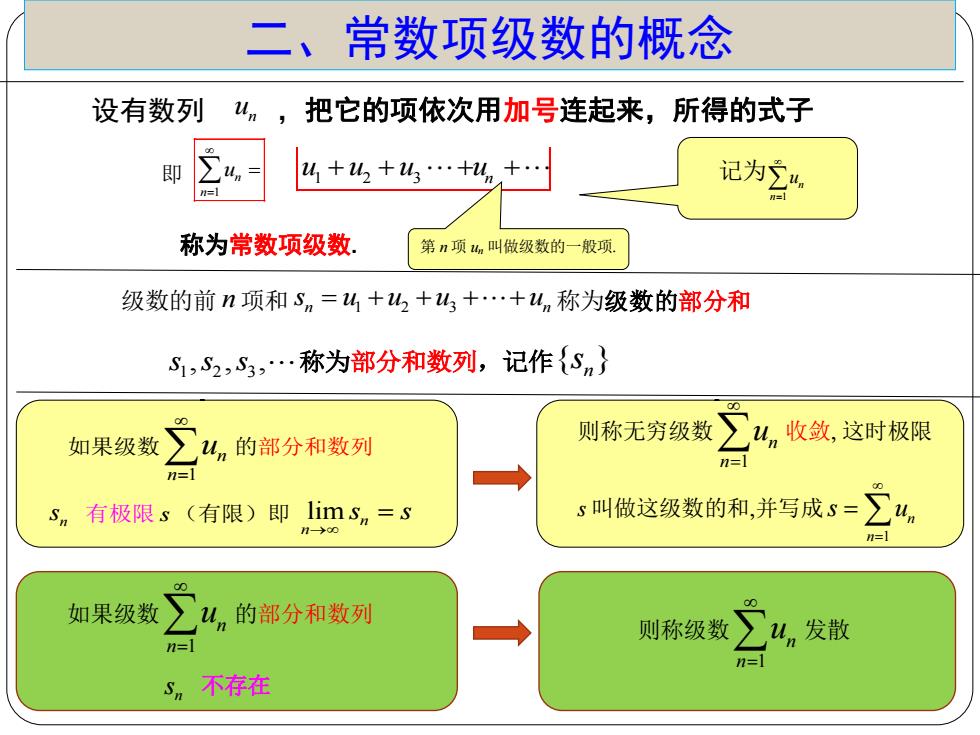
二、常数项级数的概念 设有数列 n u ，把它的项依次用加号连起来，所得的式子 1 2 3 n u u u u     称为常数项级数. 即 1 n n u     记为  n1 n u 级数的前 n 项和 n n 1 2 3 s u u u u     称为级数的部分和 第 n 项 un 叫做级数的一般项 1 2 3 s s s , , , 称为部分和数列，记作{ }n s 如果级数  n1 un 的部分和数列 n s 有极限 s （有限）即 lim n n s s   如果级数  n1 n u 的部分和数列 n s 不存在 则称无穷级数  n1 un 收敛 这时极限 s 叫做这级数的和并写成 1 n n s u     则称级数  n1 n u 发散

二、常数项级数的概念 当级数了 收敛时，其部分和sn是级数 的和s的近似值它们之间的差值 00 'n=S一Sn=4n+1+4n+2十…叫做级数 un的余项。 n=1 注记1： 级数u 收敛的充要条件是其部分和数列、收敛 n=1 级数】 发散的充要条件是其部分和s,数列发散 注记2：级数 ，收敛的充要条件是m。=s,lm=S 10 n=1 注记3：用定义判断级数 收敛的一般步骤 n=1 第一步：计算 的前n项和Sn;第二步：判断Sn是否收敛 n=

二、常数项级数的概念 当级数  n1 un 收敛时 其部分和 n s 是级数  n1 un 的和s 的近似值 它们之间的差值 n n n n 1 2 r s s u u        叫做级数  n1 un 的余项 注记 1：级数  n1 n u 收敛的充要条件是其部分和数列 n s 收敛 级数  n1 un 发散的充要条件是其部分和 n s 数列发散 注记 2：级数  n1 n u 收敛的充要条件是 2 2 1 lim ,lim n n n n s s s s      注记 3：用定义判断级数  n1 n u 收敛的一般步骤 第一步：计算  n1 n u 的前n 项和 n s ；第二步：判断 n s 是否收敛

例1讨论等比级数（几何级数） ∑ag=a+ag+ag2+…+ag+…的收敛性. n= sn=a+aq+ag+…+ag" lql≠1 a-aq" Sn= 1-q g=1 q>1 14l<1 S,=na S,=-na limg”=o∞ limg"=0 n-→c0 1-→0 lims,=o lims,=o lims,=o a 1-→c0 1→o0 1-→c0 lims,= 1-→00 1-9 q"= 当q<1时，收敛 1=0 当 ≥1时，发散

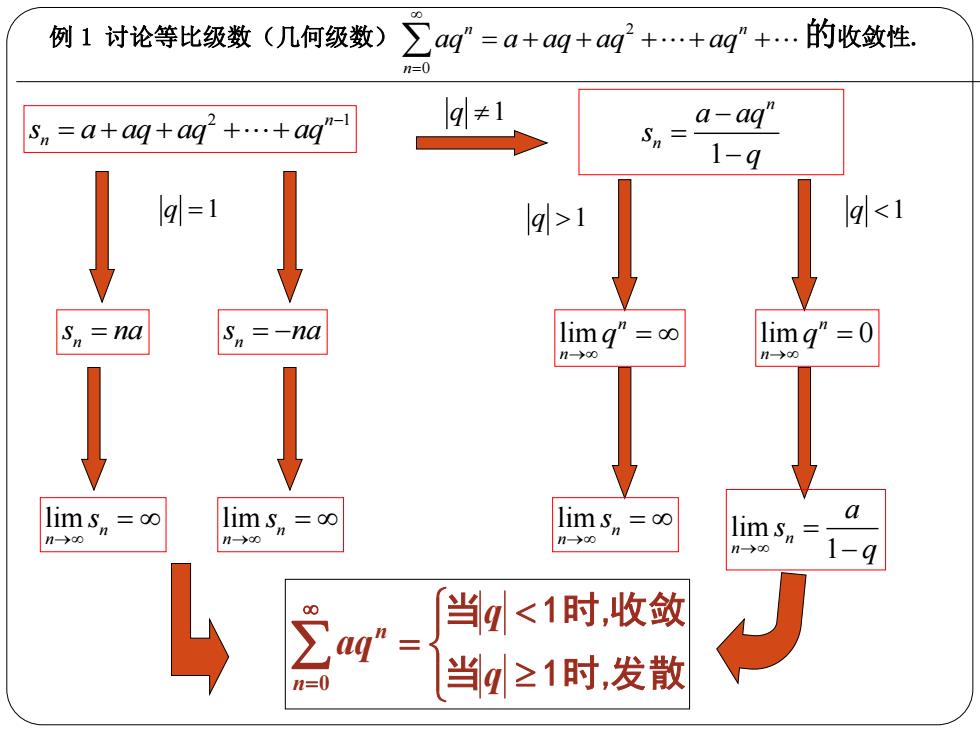
例 1 讨论等比级数（几何级数） 2 0 n n n aq a aq aq aq         的收敛性. 2 1 n n s a aq aq aq      q 1 1 n n a aq s q    q 1 n s na  lim n n s    n s na   lim n n s    q 1 lim n n q    lim n n s    q 1 lim 0 n n q   lim 1 n n a s  q             当 1时,发散 当 1时,收敛 q q aq n n 0

二、常数项级数的概念 例2判别级数乃，1=1+」 1 +…的收敛性 m后n(n+1)12'2.3 (n+1) 解： 111 显然w,Fmn+0）nn+1 拆项法 所以 1,1 1 5m=122-3 n-(n+1) (1(及+日)1中 故im5,=l,从而级数方1 收敛 7→00 台n(n+1)

二、常数项级数的概念 例 2 判别级数 1 1 1 1 1 n n n n n ( 1) 1 2 2 3 ( 1)                的收敛性 解： 显然 1 1 1 ( 1) 1 n u n n n n      所以 1 1 1 1 2 2 3 ( 1) n s n n         1 1 1 1 1 1 1 1 2 2 3 1 1 n n n                              故 lim 1 n n s   ，从而级数 1 1 n n n( 1)     收敛 拆项法

二、常数项级数的概念 例3证明调和级数2}发散 反证法 n=1 n 证明： 1++1+1十+ 1 n'n+1 2n 所以-，=1 11,1 11 十…十 2n2n 2n 2n2 如果调和级数上收敛，则im,=ms,=,从而 n=i n n-+00 m-,=m一m5=s-5=0分 n→ 7◆ 由极限的性质可得 n→ 矛盾.因此调和级数发散

二、常数项级数的概念 例 3 证明调和级数 1 1 n n    发散. 证明： 显然 1 1 1 , 2 n s n 2 1 1 1 1 1 2 1 2 n s n n n 所以 2 1 1 1 1 1 1 1 2 2 2 2 2 n n s s n n n n n 由极限的性质可得 2 1 lim 2 n n n s s 如果调和级数 1 1 n n    收敛，则 2 lim lim n n n n s s s ，从而 2 2 1 lim lim lim 0 2 n n n n n n n s s s s s s 矛盾. 因此调和级数发散. 反证法

课堂训练-判断正误 (1)-882 9+g2+…+(-1) 8+…收敛 3323” (2) 222+…+ +…发散 2n 111 (3) 一十 +…发散 363n (4)1+2+…+n+…发散. (5)-1+1-1+1-…-1+1-…发散 (6)(-1+1)+(-1+1)+…+(-1+1)…收敛

课堂训练-判断正误 （1） 2 2 8 8 8 ( 1) 9 9 9 n n n       收敛. （2） 2 2 3 3 3 2 2 2 n n     发散. （3） 1 1 1 3 6 3n     发散. （4） 1 2    n 发散. （5）        1 1 1 1 1 1 发散 （6） ( 1 1) ( 1 1) ( 1 1)         收敛

三、常数项级数收敛的必要条件 问题： 要使级数 ∑n收敛，必须满足什么条件？ Sn=41+42+%3+…+4n-1+un 级数三“收敛 S-1=山1+山2+43+…+un-1 un Sn-Sn-1 lim s=s limu lims-lim s,-1=s-s=0 n-→00 n-→0 n-→0 定理： 如果级数∑4，收敛，则1im4,=0(反过来不一定成立) n=1 11-→00 注记3：若1im4,≠0则∑4，一定发散 n-o0 n=1

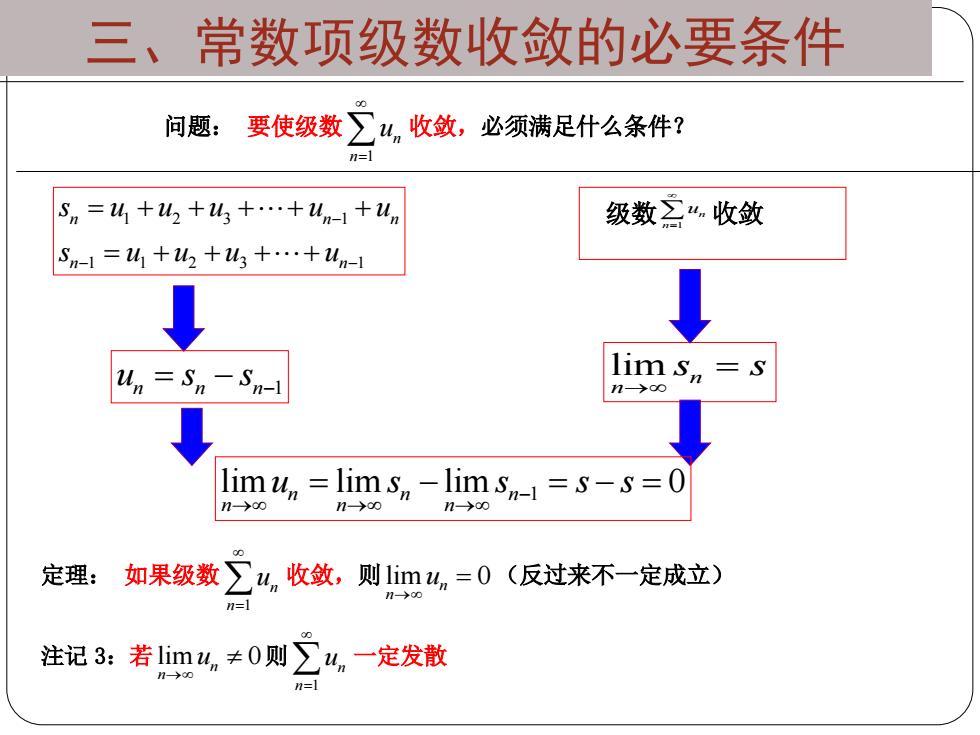
三、常数项级数收敛的必要条件 问题： 要使级数 1 n n u    收敛，必须满足什么条件？ 级数 1 n n u   1 2 3 1  收敛 1 1 2 3 1 n n n n n s u u u u u s u u u u               n n n 1 u s s    lim n n s s   1 lim lim lim 0 n n n n n n u s s s s          定理： 如果级数 1 n n u    收敛，则 lim 0 n n u   （反过来不一定成立） 注记 3：若 lim 0 n n u   则 1 n n u    一定发散

四、常数项级数基本性质 性质1：如果级数 山n收敛，且其和为s, 性质2：如果级数 ∑4n与∑yn收敛 n=1 n=l 则级数∑k,也收敛，且其和为s. 则级数∑(4士）也收敛，且 n=1 n= 0 即 n=1 n=1 性质3：在一个级数的前面加上（去掉） 性质4：如果一个级数收敛，则加括号后 有限项，级数的敛散性不变 所成的级数也收敛，且与原级数有 即 ∑4与 4n有相同的敛散性 相同的和. n= n=k+1

四、常数项级数基本性质 性质 1：如果级数  n1 un 收敛 且其和为s, 则级数 1 n n ku    也收敛且其和为ks.. 即 1 1 n n n n ku k u        性质 2：如果级数  n1 un 与 1 n n v    收敛 则级数   1 n n n u v     也收敛且 1 1 1 ( ) n n n n n n n u v u v             性质 3： 在一个级数的前面加上(去掉) 有限项 级数的敛散性不变 即 1 n n u    与 1 n n k u     有相同的敛散性 性质 4：如果一个级数收敛 则加括号后 所成的级数也收敛 且与原级数有 相同的和.