南阳师范学院：《高等数学》课程教学资源（课件讲稿）10.2 常数项级数的审敛法

第二节常数项级数的审敛法 正项级数 及审敛性 交错级数 绝对收敛 及审敛性 条件收敛

第二节 常数项级数的审敛法 交错级数 及审敛性 正项级数 及审敛性 绝对收敛 条件收敛

正项级数及其审敛法 1正项级数的定义： 若4n≥0(n=1,2,3,),则∑4，称为正项级数 正项级数的各项 正项级数的部分和 都是正数零 数列单调递增 2.正项级数收敛的充要条件 定理1正项级数收敛的充要条件是部分和数列sn有界 问题1：若0≤n≤yn=1,2,),问 (1)当级数收敛时，级数4，是收敛还是发散？ (2)当级数，发散时，级数，是收敛还是发散？

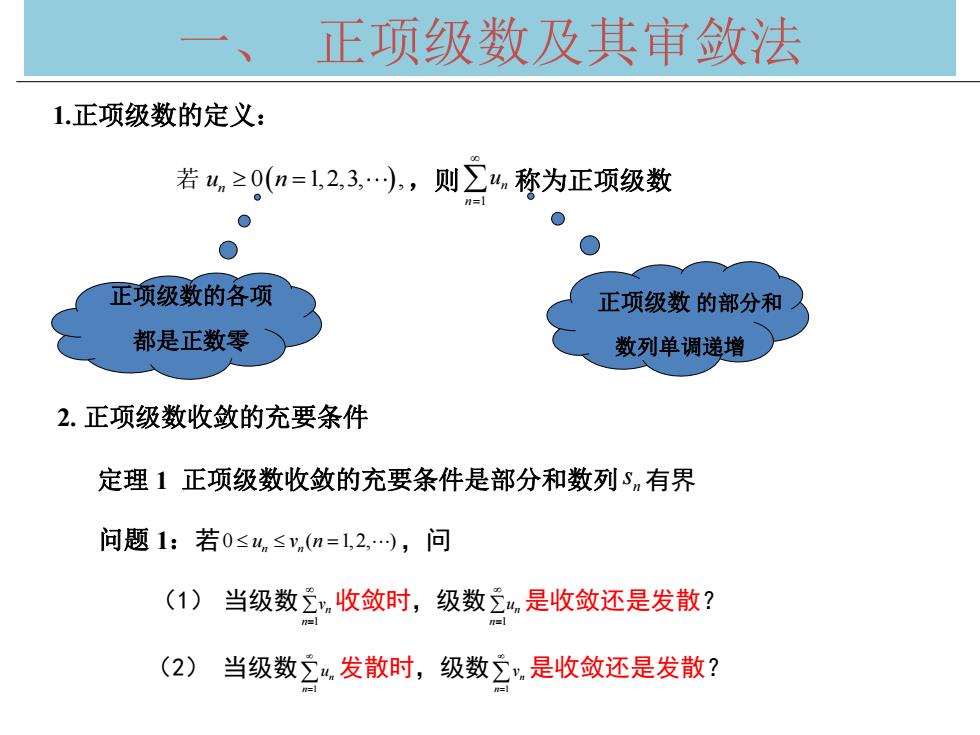
一、 正项级数及其审敛法 1.正项级数的定义： 正项级数 的部分和 数列单调递增 若 u n n   0 1,2,3, ,   ，则  n1 un 称为正项级数 2. 正项级数收敛的充要条件 正项级数的各项 都是正数零 定理 1 正项级数收敛的充要条件是部分和数列 n s 有界 问题 1：若0 ( 1,2, ) n n     u v n ，问 （1） 当级数   n1 n v 收敛时，级数   n1 n u 是收敛还是发散？ （2） 当级数 1 n n u    发散时，级数 1 n n v    是收敛还是发散？

正项级数及其审敛法 分析：设n与u,的部分和数列分别为w, 若级数，收敛 w有界，即存在正数M, 使得w,≤M sn≤M.E 即2，的部分和数列有界.从而u,收敛 三 3.比较审敛法口诀：大收敛，则小收敛 小发散，则大发散 设4n和2yn都是正项级数且4，≤y.(n=1,2,)设4n和yn都是正项级数且wn≤，(k>0,n>N (1) 若级数收敛，则级数2u收敛； (1) 若级数收敛，则级数u收敛； (2) 若级数4，发散，则级数y,发散 (2) 若级数4发散，则级数，发散

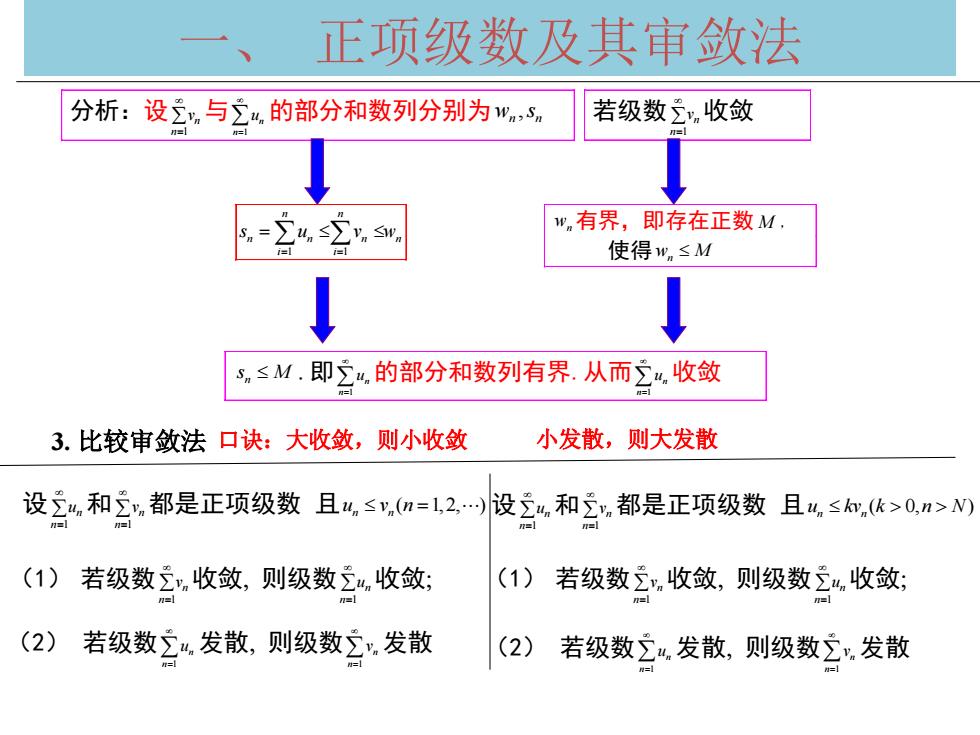
一、 正项级数及其审敛法 分析：设   n1 n v 与 1 n n u    的部分和数列分别为 , w s n n 1 1 n n n n n n i i s u v w        若级数  n1 n v 收敛 wn 有界，即存在正数M ， 使得w M n  n s M .即 1 n n u    的部分和数列有界.从而 1 n n u    收敛 3. 比较审敛法 设   n1 n u 和   n1 n v 都是正项级数 且 ( 1,2, ) n n u v n    （1） 若级数   n1 n v 收敛 则级数   n1 un 收敛 （2） 若级数 1 n n u    发散 则级数 1 n n v    发散 设   n1 un 和   n1 n v 都是正项级数 且 ( 0, ) n n u kv k n N    （1） 若级数   n1 n v 收敛 则级数   n1 un 收敛 （2） 若级数 1 n n u    发散 则级数 1 n n v    发散 口诀：大收敛，则小收敛 小发散，则大发散

例1讨论p-级数。p>0的收敛性. p≤1 D>1 1 设∑ 的部分和数列为s =2 (n-1)p-I =ks∫ (n+1) ↓ 发 lims,=lim -→0 (n+1)P- 发散 收敛， 由比较审敛法可知乃」 h 收敛 注记3 p-级数是与广义积分具有相同的敛散性

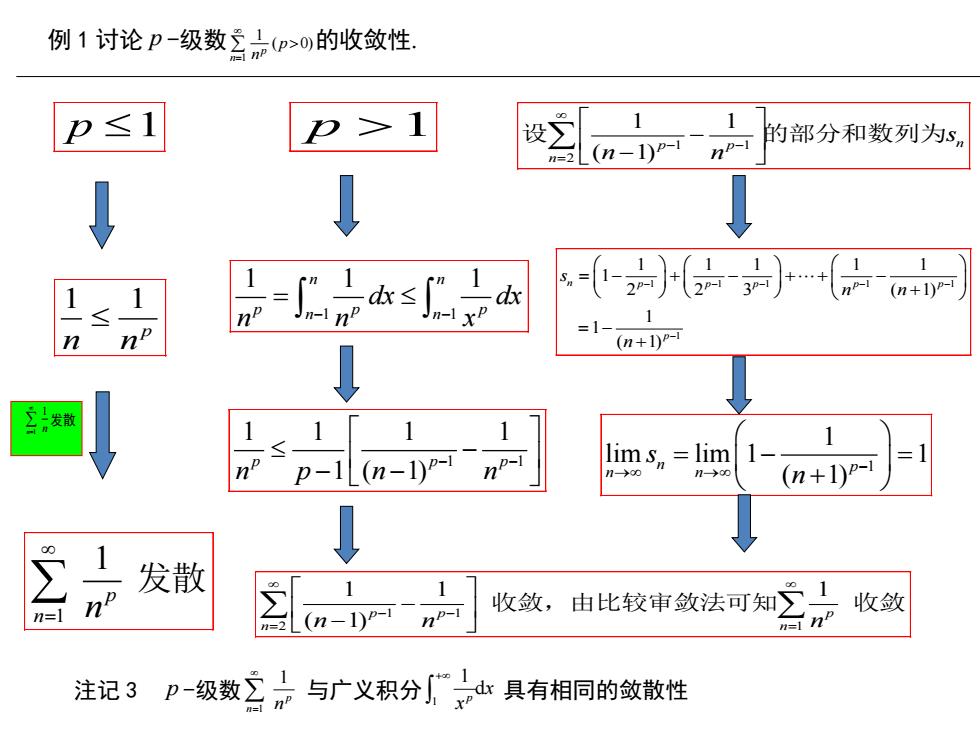
例 1 讨论 p -级数 ( 0) 1 1     p n p n 的收敛性  p 1 p 1 1 1 p n n  1 1 n n   发散 1 1 1 1 1 n n p p p n n dx dx n n x       1 1 1 1 1 1 1 ( 1) p p p n p n n             1 1 2 1 1 ( 1) p p n n s n n             设 的部分和数列为 1 1 1 1 1 1 1 1 1 1 1 1 2 2 3 ( 1) 1 1 ( 1) n p p p p p p s n n n                                     1 1 lim lim 1 1 ( 1) n p n n s n              1 1 2 1 1 1 1 ( 1) p p p n n n n n                 收敛，由比较审敛法可知 收敛 1 1 p n n    发散 注记 3 p -级数 1 1 p n n    与广义积分 1 1 d p x x   具有相同的敛散性

正项级数及其审敛法 注记1：比较审敛法的前提是必须有一个已知敛散性的级数作为参考级数 常用的基本级数是等比级数或调和级数或p级数 (1)当4<1时，等比级数∑g收敛；当4=1时，等比级数三g发散； (2)当P≤1一级数空发散：智)1级数空品收敛 注记2利用比较审敛法判断正项级数敛散性的思路 第一步：对给出的级数的通项进行适当的放大与缩小得到一个新数列 第二步：判断以新的的数列为通项的级数的敛散性 第三步：利用“大者收敛则小者也收敛，小者发散则大者也发散“得出结论

一、 正项级数及其审敛法 注记 1：比较审敛法的前提是必须有一个已知敛散性的级数作为参考级数 常用的基本级数是等比级数或调和级数或 p-级数 （1）当 q 1 时，等比级数 1 n n q    收敛；当 q =1 时，等比级数 1 n n q    发散； 注记 2 利用比较审敛法判断正项级数敛散性的思路 第一步：对给出的级数的通项进行适当的放大与缩小得到一个新数列 第二步：判断以新的的数列为通项的级数的敛散性 第三步：利用 “大者收敛则小者也收敛，小者发散则大者也发散“得出结论 （2）当 p 1时， p-- 级数 1 1 p n n    发散；当 p 1时， p-- 级数 1 1 p n n    收敛 （2）

正项级数及其审敛法 比较审敛法常用的基本级数是等比级数或调和级数或P一级数 例1判断级数2n的收敛性 例2证明级数云 1云的收敛。 分析：(1)观察级数三n虽然不是等比级分析：(1)观察级数三与级数 n(n+) 数，但与等比级数三会形式相似 (n+1) 形式相似 (2)找出三2十，的通项与等比级数 (2)找出d的通项与级数含 芸通项的关系0≤2n5 2”-n2 通项的关系 *可产a+iW+nn+>0 (3)判断等比级数三的收敛性 (3)判断级数2 1 Vn+1) 的收敛性 (4）利用大收敏则小收敛判名的收敛性 (4)利用小发散则大发散判断2一的收敛性

一、 正项级数及其审敛法 比较审敛法常用的基本级数是等比级数或调和级数或 p-级数 例 1 判断级数 1 1 2 n n n     的收敛性 分析：（1）观察级数 1 1 2 n n n     虽然不是等比级 数，但与等比级数 1 1 2 n n    形式相似 （2）找出 1 1 2 n n n     的通项与等比级数 1 1 2 n n    通项的关系 （3）判断等比级数 1 1 2 n n    的收敛性 （4）利用大收敛则小收敛判断 1 1 2 n n n     的收敛性 例 2 证明级数 1 1 n n n( 1)     的收敛 分析：（1）观察级数 1 1 n n n( 1)     与级数   2 1 1 n n 1     形式相似 （2）找出 1 1 n n n( 1)     的通项与级数   2 1 1 n n 1     通项的关系 （3）判断级数   2 1 1 n n 1     的收敛性 （4）利用小发散则大发散判断 1 1 n n n( 1)     的收敛性 1 1 0 2 2 n n n    1 1 1 0 n n n n ( 1) ( 1)( 1) n 1       

正项级数及其审敛法 5极限审敛法 设2，是正项级数 V=- （1)如果1im,=>0(或1im,=+o),则级数24，发散 Vn=- (2)如果p>1,而lim npi4,=l0≤11.由极限审敛法可知 级数2m-1 白+2n+3发散 级数 cos(a≠0)收敛

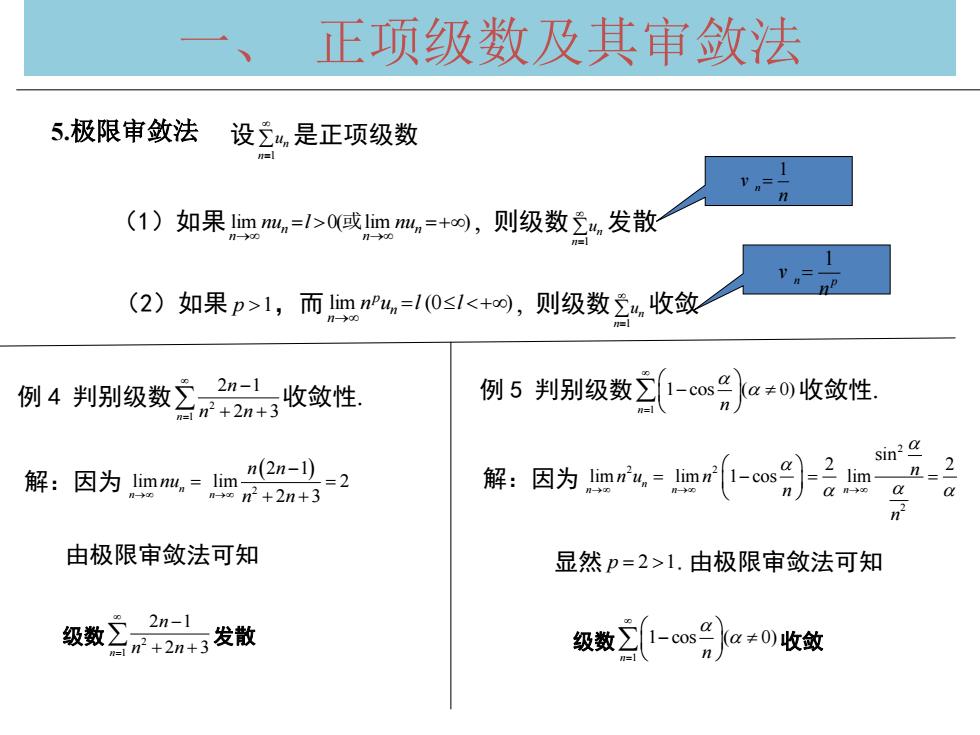
一、 正项级数及其审敛法 5.极限审敛法 设   n1 n u 是正项级数 （1）如果 lim  0( lim )   n n n n nu l 或 nu  则级数   n1 un 发散 （2）如果 p 1，而 lim  (0 )  n u l l n p n  则级数   n1 un 收敛 例 4 判别级数 2 1 2 1 n 2 3 n n n       收敛性 例 5 判别级数 1 1 cos ( 0) n n              收敛性 解：因为   2 2 1 lim lim 2 2 3 n n n n n nu   n n      由极限审敛法可知 级数 2 1 2 1 n 2 3 n n n       发散 解：因为 2 2 2 2 sin 2 2 lim lim 1 cos lim n n n n n n u n n n                   显然 p   2 1.由极限审敛法可知 级数 1 1 cos ( 0) n n              收敛 1 n v n  1 n p v n 

正项级数及其审敛法 6.比值审敛法 例6：判断正误(1)号收敛(2)空器发散 设u,>0,且1imau=p,则 n un 解（1) 因为+ (1)当p1（或m=)时级数发散： 10* n! m-→10 所以级数云发散 (3)当p=1时级数可能收敛也可能发散 例7：证明一=0 如级数户。一收敛，但 台2n-(2n-1) 证明：显然%兴0且m=一“)广=e =1 这时p=e<1由比值审敛法可得级数收敛 所以 lim n! 0

一、 正项级数及其审敛法 6.比值审敛法 设 0, n u  且    n n n u u 1 lim  则 （1）当  1时级数收敛 （2）当  1 (或    n n n u u 1 lim )时级数发散 （3）当  1时级数可能收敛也可能发散 如级数 1 1 2 (2 1) n n n 收敛，但 1 (2 1) 2 lim lim 1 (2 1) (2 2) n n n n u n n u n n 例 6：判断正误（1） 2 1 3 n n n 收敛 （2） 1 ! 10n n n 发散 解 （1）因为 2 1 1 1 1 lim lim 1 1 3 3 n n n n u u n              所以级数 2 1 3 n n n 收敛 （2）因为 1 1 ( 1)! 10 1 lim lim lim 10 ! 10 n n n n n n n u n n u n                   所以级数 1 ! 10n n n 发散 例 7：证明 ! lim 0 n n n  n  证明：显然 ! 0 n n n u n   且 1 1 lim lim 1 n n n n n u n e u n              这时 1  e 1    由比值审敛法可得级数 1 ! n n n n    收敛 所以 ! lim 0 n n n  n 

交错级数及其审敛法 1交错级数的定义：各项正负交错的级数称为交错级数.一般形式为--，其中4，>0. 2.交错级数审敛法（莱布尼茨定理） 例8证明级数-yL收敛，并估计和及余项， 如果交错级数-ly-u,满足条件： 证 显然这是一个交错级数.因为此级数满足 (1)1≤，(n=l2,）(通项单调递减)； 1)441 <=4 limu,lim-=0 ntl n 1→n 所以级数2-收敛 (2) lim un=0 n-→0 则 (1)级数收敛 (2)其和s≤1 (2)其和s≤4 (3)其余项n的绝对值n长u1= n+1 (3)其余项n的绝对值≤4

二、 交错级数及其审敛法 1.交错级数的定义：各项正负交错的级数称为交错级数.一般形式为     1 1 ( 1) n n n u  其中 un 0  2.交错级数审敛法（莱布尼茨定理） 如果交错级数      1 1 ( 1) n n n u 满足条件 （1） 1 ( 1,2, ) n n u u n     (通项单调递减) （2） lim 0  n n u 则 （1）级数收敛 （2）其和 1 s u  （3）其余项 n r 的绝对值 n n 1 r u   例 8 证明级数 1 ( 1) 1 1      n n n 收敛 并估计和及余项 证 显然这是一个交错级数 因为此级数满足 所以级数 1 ( 1) 1 1      n n n 收敛 （2）其和 s 1 （3）其余项 n r 的绝对值 1 1 | | 1 n n r u n     （1） 1 1 1 1 , lim lim 0 1 n n n n n u u u n n n         

三、绝对收敛与条件收敛 1.绝对收敛与条件收敛的定义 若级数收敛，则称级数，绝对收敛 若级数24，收敛，而级数2u发散，则称级2条件收敛 例9试判断级数立-p>o的收敛性 解：(1)当p>1时.由于p-级数之收癫以.立-绝对收敛 (2)当0是交错级数，且满足 (n+1)驴产=，lim,=lim 11 1 4n+1 =0 0 n-onp 所以-re>收敛.因此级数立-r>0条件收敛

三、 绝对收敛与条件收敛 1..绝对收敛与条件收敛的定义 若级数   1 | | n n u 收敛 则称级数   n1 n u 绝对收敛 若级数   n1 n u 收敛 而级数   1 | | n n u 发散 则称级   n1 n u 条件收敛 例 9 试判断级数 1 1 1 ( 1)n p n n      ( 0) p  的收敛性 解：（1）当 p 1 时，由于 p-- 级数 1 1 p n n    收敛，所以， 1 1 1 ( 1)n p n n      绝对收敛 （2）当 0 1   p 时， p-- 级数 1 1 p n n    发散，显然 1 1 1 ( 1)n p n n      ( 0) p  是交错级数，且满足   1 1 1 1 ,lim lim 0 1 n n n p p p n n u u u n n n          所以 1 1 1 ( 1)n p n n      ( 0) p  收敛.因此级数 1 1 1 ( 1)n p n n      ( 0) p  条件收敛