§8.7多元函数的极值及算法 多元函数极值 的应用 多元函数的极 主要 多元函数的条 值 内容 件极值 多元函数的 最值
§8.7 多元函数的极值及算法 多元函数的极 值 多元函数的条 件极值 多元函数极值 的应用 多元函数的 最值 主要 内容
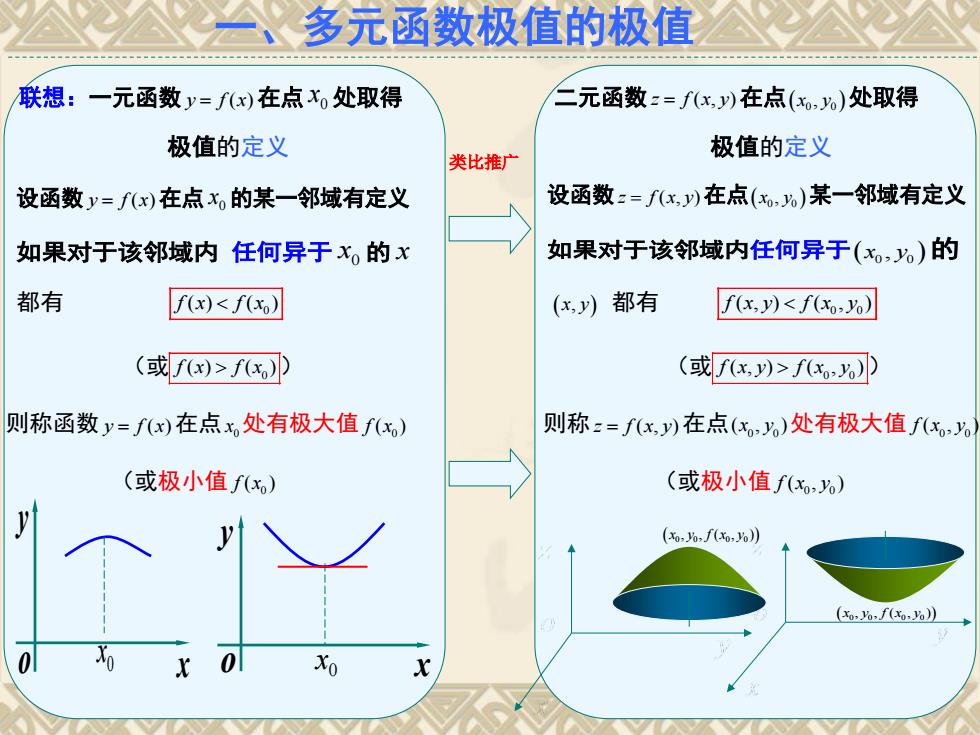
多元函数极值的极值 联想:一元函数y=fx)在点x处取得 二元函数:=fx,)在点(x,)处取得 极值的定义 类比推广 极值的定义 设函数y=fx)在点x的某一邻域有定义 设函数:=fx,y)在点(x,)某一邻域有定义 如果对于该邻域内任何异于x,的x 如果对于该邻域内任何异于(x。)的 都有 f(x)fx)) (或fx)>fx) 则称函数y=fx)在点x,处有极大值f(x) 则称:=fx,y)在点(x,)处有极大值fx (或极小值fx) (或极小值fx) y (x0,6,f(,6) (xo,%,f(,%)) 0 0 Xo
一、多元函数极值的极值 联想:一元函数 y f x ( )在点 0 x 处取得 极值的定义 类比推广 设函数 y f x ( )在点 0 x 的某一邻域有定义 如果对于该邻域内 任何异于 0 x 的 x 都有 0 f x f x ( ) ( ) (或 0 f x f x ( ) ( ) ) 则称函数 y f x ( )在点 0 x 处有极大值 0 f x( ) (或极小值 0 f x( ) x y o 0 x x y o 0 x 二元函数z f x y ( , )在点 x y 0 0 , 处取得 极值的定义 设函数z f x y ( , )在点 x y 0 0 , 某一邻域有定义 如果对于该邻域内任何异于 x y 0 0 , 的 x y, 都有 0 0 f x y f x y ( , ) ( , ) (或 0 0 f x y f x y ( , ) ( , ) ) 则称 z f x y ( , )在点 0 0 ( , ) x y 处有极大值 0 0 f x y ( , ) (或极小值 0 0 f x y ( , ) x y f x y 0 0 0 0 , , ( , ) x y f x y 0 0 0 0 , , ( , )
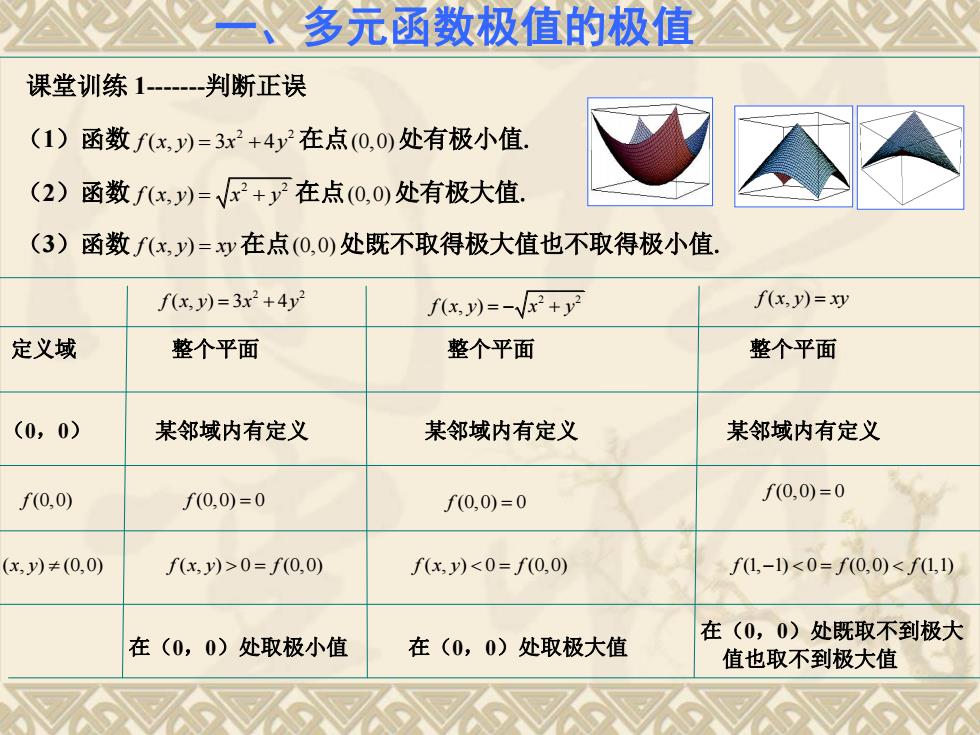
多元函数极值的极值 课堂训练1--判断正误 (1)函数fx,)=3x2+4y2在点(0,0)处有极小值. (2)函数fx,y)=√x2+y在点(0,0)处有极大值, (3)函数fx,)=y在点(0,0)处既不取得极大值也不取得极小值. fx,y)=3x2+4y2 fx,)=-√2+y f(x,y)=xy 定义域 整个平面 整个平面 整个平面 (0,0) 某邻域内有定义 某邻域内有定义 某邻域内有定义 f(0,0) f(0,0)=0 f(0,0)=0 f(0,0)=0 (x,y)≠(0,0) f(x,y)>0=f0,0) f(x,y)<0=f(0,0) fL1,-1)<0=f0,0)<f1,1) 在(0,0)处既取不到极大 在(0,0)处取极小值 在(0,0)处取极大值 值也取不到极大值
课堂训练 1-------判断正误 (1)函数 2 2 f x y x y ( , ) 3 4 在点(0,0)处有极小值 (2)函数 2 2 f x y x y ( , ) 在点(0,0)处有极大值 (3)函数 f x y xy ( , ) 在点(0,0)处既不取得极大值也不取得极小值 2 2 f x y x y ( , ) 3 4 2 2 f x y x y ( , ) f x y xy ( , ) 定义域 整个平面 整个平面 整个平面 (0,0) 某邻域内有定义 某邻域内有定义 某邻域内有定义 f (0,0) 0 f (0,0) 0 f (0,0) 0 ( , ) (0,0) x y f x y f ( , ) 0 (0,0) f x y f ( , ) 0 (0,0) f f f (1, 1) 0 (0,0) (1,1) 在(0,0)处取极小值 在(0,0)处取极大值 在(0,0)处既取不到极大 值也取不到极大值 f (0,0) 一、多元函数极值的极值

多元函数极值的极值 联想:一元函数y=f(x)在点Xo 类比猜测 二元函数:=f(x,y)在点(x%) 处取得极值的必有条件 处取得极值的必有条件 定理1 设函数y=f(x)在点x可导 设函数:=∫x,)在点(x) 若该函数在x,处取得极值 类比清测 有偏导数,若对该函数在 则必有 (,%)取得极值,则必有 f(x)=0 f(6)=0,f(x6)=0 满足该方程的点称为驻点 满足该方程的点称为驻点
一、多元函数极值的极值 联想:一元函数 y f x ( ) 在点 0 x 处取得极值的必有条件 设函数 y f x ( )在点 0 x 可导 若该函数在 0 x 处取得极值 则必有 0 f x ( ) 0 满足该方程的点称为驻点 二元函数 z f x y ( , )在点 x y 0 0 , 处取得极值的必有条件 类比猜测 设函数z f x y ( , )在点 x y 0 0 , 有偏导数,若对该函数在 x y 0 0 , 取得极值,则必有 0 0 0 0 ( , ) 0, ( , ) 0 x y f x y f x y 满足该方程的点称为驻点 类比猜测 定理 1
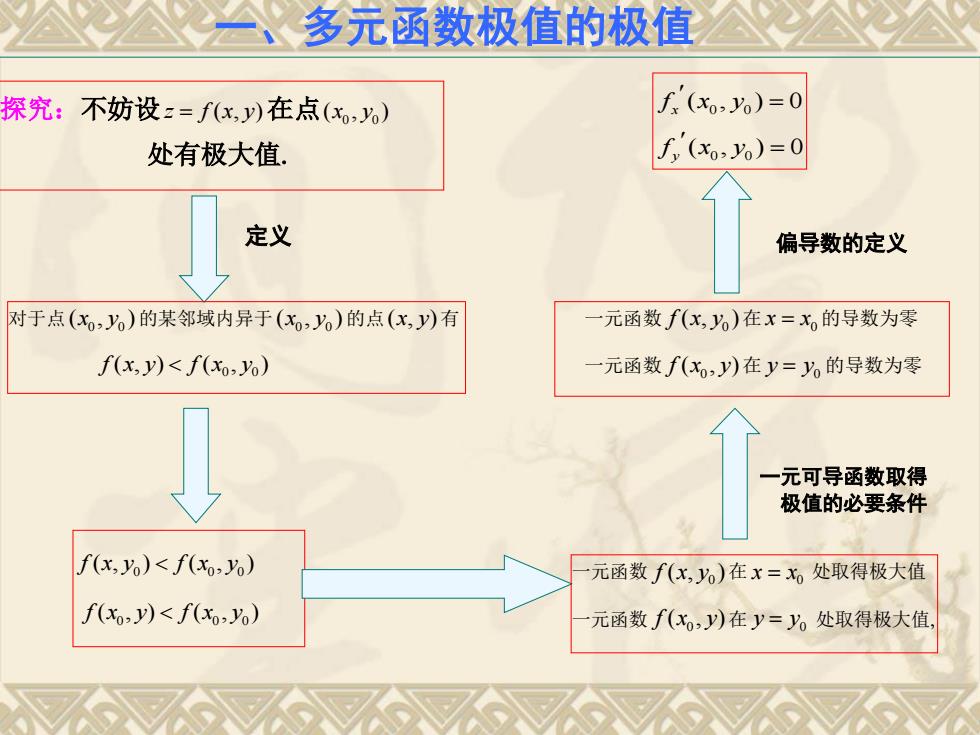
多元函数极值的极值 探究:不妨设z=f(x,y)在点(x) f (xo2 o)=0 处有极大值. f(xo,)=0 定义 偏导数的定义 对于点(x,y)的某邻域内异于(x,0)的点(x,y)有 元函数f(x,y)在x=x的导数为零 f(x,y)Yo) 元函数f(x,y)在x=x处取得极大值 f(Xo-y)Yo) 元函数f(xo,y)在y=y。处取得极大值
探究:不妨设z f x y ( , )在点 0 0 ( , ) x y 处有极大值 对于点 0 0 ( , ) x y 的某邻域内异于 0 0 ( , ) x y 的点 ( , ) x y 有 0 0 f x y f x y ( , ) ( , ) 0 0 0 f x y f x y ( , ) ( , ) 0 0 0 f x y f x y ( , ) ( , ) 定义 一元函数 0 f x y ( , )在 0 x x 处取得极大值 一元函数 0 f x y ( , )在 0 y y 处取得极大值 一元函数 0 f x y ( , )在 0 x x 的导数为零 一元函数 0 f x y ( , )在 0 y y 的导数为零 一元可导函数取得 极值的必要条件 偏导数的定义 0 0 0 0 ( , ) 0 ( , ) 0 x y f x y f x y 一、多元函数极值的极值

、多元函数极值的极值 定理2(充分条件)设函数:=f(x,)在点(x,)的某邻域内有连续的一阶和二阶偏导数.且 f(x)=0,f(x0,%)=0 记 f(x,%)=Af0(x0,6)=Bf(x,%)=C (1)当4C-B>0时,函数fx,)在点()处具有极值,且 当A0时函数f(x,)在点(x,%)处有极小值 (2)当4C-B<0时,函数fx,y)在点(x,)处没有极值 (3)当4C-B=0时,函数fx,)在点(x,)处可能有极值也可能没有极值
定理 2(充分条件) 设函数z f x y ( , )在点 0 0 ( , ) x y 的某邻域内有连续的一阶和二阶偏导数 .且 记 0 0 ( , ) xx f x y A 0 0 ( , ) xy f x y B 0 0 ( , ) yy f x y C 0 0 ( , ) 0 x f x y , 0 0 ( , ) 0 y f x y (1)当 2 AC B 0时,函数 f x y ( , )在点 0 0 ( , ) x y 处具有极值 且 当 A 0时函数 f x y ( , )在点 0 0 ( , ) x y 处有极大值 当 A 0 时函数 f x y ( , )在点 0 0 ( , ) x y 处有极小值 (2)当 2 AC B 0时,函数 f x y ( , )在点 0 0 ( , ) x y 处没有极值 (3)当 2 AC B 0 时,函数 f x y ( , )在点 0 0 ( , ) x y 处可能有极值也可能没有极值 一、多元函数极值的极值

多元函数极值的极值 注记3:求z=f(x,y)极值的步骤 例2求函数fx,)=x-y2+3x2+3y2-9x的极值, 第一步:求出f(x,y),f(x,) 解 (1)显然f(x,y)=3x2+6x-9,f(x,)=-3y2+6y 第二步:解方程组)=0 (x.y)=0 求出驻点(x) (2)解方程组 fx,川=3x+6x-9=得x=3 f,(x,y)=-3y2+6y=0 y=0,2 第三步:求出后(x,后x,),(x,) 第四步:求出4,B,C及AC-B 于是得四个驻点为(1,0)、(1,2)、(-3,0)、(-3,2) (3)显然二阶偏导数 A=f(0,6),B=f(x0%),C=f(x) f(x,y)=6x+6,f"(x,y)=0,fw(x,y)=6y+6 第五步:根据AC-B及A的符号判断 (】 (4.0) 0,2) (-3,0 (-32 f(xy)在点(xo,)处是否取 A=f(x,)=6x+6 12>0 12>0 -120 -720 在(-3,2)处有极大值f(-3,2)=31 极小值 极大值 foo) 无极值 无极值 点(1,2),(-3,0)不是极值点
注记 3:求 z f x y ( , )极值的步骤 第一步 :求出 ( , ), ( , ) x y f x y f x y 第二步:解方程组 ( , ) 0 ( , ) 0 x y f x y f x y 求出驻点 0 0 ( , ) x y 第三步: 求出 ( , ), ( , ), ( , ) xx xy yy f x y f x y f x y 第四步: 求出 A B C , , 及 2 AC B 0 0 0 0 0 0 ( , ), ( , ), ( , ) A f x y B f x y C f x y xx xy yy 第五步:根据 2 AC B 及 A的符号判断 f x y ( , )在点 0 0 ( , ) x y 处是否取 得极值是极大还是极小 例 2 求函数 3 3 2 2 f x y x y x y x ( , ) 3 3 9 的极值 解 (1)显然 2 ( , ) 3 6 9 x f x y x x , 2 ( , ) 3 6 y f x y y y (2)解方程组 2 2 ( , ) 3 6 9 0 ( , ) 3 6 0 x y f x y x x f x y y y 得 1, 3 0,2 x y 于是得四个驻点为(1 0)、(1 2)、(3 0)、(3 2) (3)显然二阶偏导数 f x y x f x y f x y y xx xy yy ( , ) 6 6, ( , ) 0, ( , ) 6 6 0 0 ( , ) x y (1,0) (1,2) ( 3,0) ( 3,2) ( , ) 6 6 A f x y x xx 12 0 12 0 12 0 12 0 ( , ) 0 B f x y xy 0 0 0 0 ( , ) 6 6 C f x y y yy 6 -6 6 -6 2 AC B 72 0 72 0 72 0 72 0 0 0 f x y ( , ) 极小值 5 无极值 无极值 极大值31 函数在(1,0)处有极小值 f (1,0) 5 , 在( 3,2) 处有极大值 f ( 3,2) 31 点(1,2),( 3,0) 不是极值点 一、多元函数极值的极值

多元函数的最值 回顾:如果一元fx)在有界闭区间D上连续,则 推广:如果二元fx,y)在有界闭区域D上连续,则 (x)在D上必定能取得最大值和最小值. f(x,y)在D上必定能取得最大值和最小值. 注记1:一元函数的最大值或最小值的点既可 注记1:二元函数的最大值或最小值的点既可 能在驻点上取到,也可能在不可导的 能在驻点上取到,也可能在偏导数不 点或端点上取到. 存在点或边界点上取到. 注记2:求一元函数可微最大值和最小值的步骤: 注记2:求二元函数可微最大值和最小值的步骤 (1)求出函数fx)在定义域D内的所有驻点 (1)求出函数f(x,)在定义域D内的所有驻点 (2)求出函数f(x)在端点的函数值 (2)求出函数f(x,y)在边界上的最值 (3)比较函数f(x)在端点的函数值及驻点的 (3)比较函数fx,)在边界上的最值及驻点的 函数值,确定最大值和最小值 函数值,确定最大值和最小值
二、 多元函数的最值 回顾:如果一元 f x( )在有界闭区间 D 上连续,则 f x( )在 D 上必定能取得最大值和最小值 推广:如果二元 f x y ( , )在有界闭区域 D 上连续,则 f x y ( , )在 D 上必定能取得最大值和最小值 注记 1:一元函数的最大值或最小值的点既可 能在驻点上取到,也可能在不可导的 点或端点上取到 注记 1:二元函数的最大值或最小值的点既可 能在驻点上取到,也可能在偏导数不 存在点或边界点上取到 注记 2:求一元函数可微最大值和最小值的步骤 (1)求出函数 f x( )在定义域 D 内的所有驻点 (2)求出函数 f x( )在端点的函数值 (3)比较函数 f x( )在端点的函数值及驻点的 函数值,确定最大值和最小值 注记 2:求二元函数可微最大值和最小值的步骤 (1)求出函数 f x y ( , )在定义域 D 内的所有驻点 (2)求出函数 f x y ( , )在边界上的最值 (3)比较函数 f x y ( , )在边界上的最值及驻点的 函数值,确定最大值和最小值

二 公多元函数的最值 例3:求f(x,y)=x2y(4-x-y)在直线x+y=6与x轴例4要用铁板做一个体积为2m3的有盖长方体水 x轴和y轴所围成的闭区域D上的最大值与最小值 箱,问长宽高各取怎样的尺寸时用料最省? 解:(1)显然f(x,y)=2xy(4-x-y)-x2y 解:设长宽分别为xm和ym,则高为2m.因此 f(x.y)=x(4-x-y)-xy 水箱用料的面积 (2)令=0,=0得=2 x+y=6 y=1 2 (x>0,y>0) (3)显然在x轴y=0和y轴x=0上fx,y)=0 在直线x+y=6上fx,y)=-2x2(6-x) 令 4=2引o4=x}0 令 f'(x)=4x(x-6)+2x2=0 得 x1=0,x2=4, 得 x=迈,y=2,2=2 故 片=6-x1=6,y2=6-x2=2 根据题意可知材料面积的最小值一定存在,并且 显然 f(x,4)=0,f(x2,y2)=64 在D:x>0,y>0内取得,又函数在D内只有一个驻 (4) 比较后可知 f最大(2,)=4 f最小(4,2)=-64 点,因此可以断定,当长宽高均迈时A取得最小
二、 多元函数的最值 例 3:求 2 f x y x y x y ( , ) 4 在直线 x y 6与 x 轴 x y o x y 6 解:(1)显然 2 ( , ) 2 4 x f x y xy x y x y 2 2 f x y x x y x y y ( , ) 4 (2)令 ( , ) 0 ( , ) 0 x y f x y f x y , 得 2 1 x y (3)显然在 x 轴 y 0和 y 轴 x 0上 f x y ( , ) 0 在直线 x y 6上 2 f x y x x ( , ) 2 6 令 2 f x x x x ( ) 4 6 2 0 得 1 2 x x 0, 4, 故 y x y x 1 1 2 2 6 6, 6 2 显然 1 1 2 2 f x y f x y ( , ) 0, ( , ) 64 (4) 比较后可知 f最小(4,2) 64 f最大(2,1) 4 x 轴和 y 轴所围成的闭区域 D 上的最大值与最小值 例 4 要用铁板做一个体积为 3 2m 的有盖长方体水 箱,问长宽高各取怎样的尺寸时用料最省? 解:设长宽分别为 xm和 ym ,则高为 2 m xy .因此 水箱用料的面积 2 2 A xy y x x y 2 ( 0, 0) xy xy 令 2 2 2 2 2 0 2 0 A y A x x y x y , 得 3 3 x y 2, 2 , 2 3 2 xy 根据题意可知材料面积的最小值一定存在 并且. 在D x y : 0, 0 内取得 又函数在 D 内只有一个驻 点,因此可以断定 当长宽高均 3 2 时 A取得最小
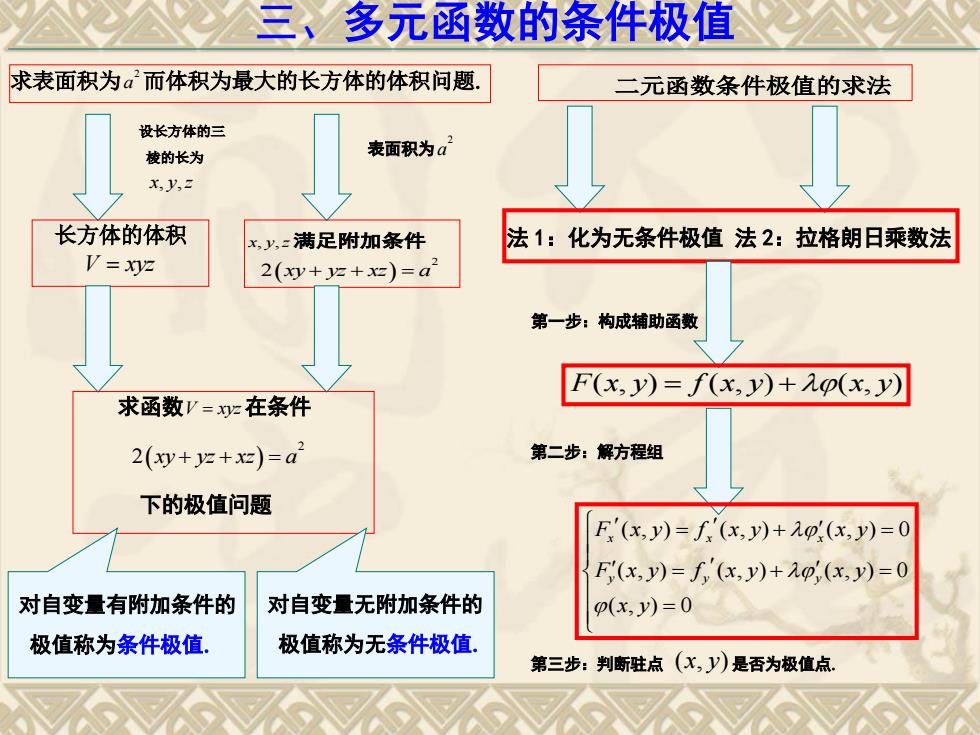
三、多元函数的条件极值 求表面积为而体积为最大的长方体的体积问题. 二元函数条件极值的求法 设长方体的三 棱的长为 表面积为a x,y,2 长方体的体积 x,y,=满足附加条件 法1:化为无条件极值法2:拉格朗日乘数法 V=xyz 2(y+z+x)=a2 第一步:构成辅助函数 F(x,y)=f(x,y)+p(x,y) 求函数V=z在条件 2(x++x)=a2 第二步:解方程组 下的极值问题 F'(x,y)=f'(x,y)+p(x,y)=0 F(x,y)=f'(x,y)+元0,(x,y)=0 对自变量有附加条件的 对自变量无附加条件的 p(x,y)=0 极值称为条件极值, 极值称为无条件极值。 第三步:判断驻点(X,y)是否为极值点
三、多元函数的条件极值 求表面积为 2 a 而体积为最大的长方体的体积问题 设长方体的三 棱的长为 x y z , , 长方体的体积 V xyz 表面积为 2 a x y z , , 满足附加条件 2 2 xy yz xz a 求函数 V xyz 在条件 2 2 xy yz xz a 下的极值问题 对自变量有附加条件的 极值称为条件极值 对自变量无附加条件的 极值称为无条件极值 二元函数条件极值的求法 法 1:化为无条件极值 法 2:拉格朗日乘数法 第一步:构成辅助函数 F x y f x y x y ( , ) ( , ) ( , ) 第二步:解方程组 ( , ) ( , ) ( , ) 0 ( , ) ( , ) ( , ) 0 ( , ) 0 x x x y y y F x y f x y x y F x y f x y x y x y 第三步:判断驻点 ( , ) x y 是否为极值点