
§9.3 二重积分的应用 体积的 面积的 计 算 计算 反常积分 的计算
§9.3 二重积分的应用 体积的 计 算 面积的 计 算 反常积分 的计算

曲顶柱体体积的计算 回顾: 二重积分的几何意义 注记1:求曲顶柱体体积的一般步骤 (1)如果fx,y)≥0,二重积分fx,y1o 第一步:画出曲顶柱体围成的几何草图 就是曲顶柱体的体积. 第二步:确定曲顶柱体的曲顶及区边表达式 (2)如果fx,y)<0,二重积分∬fx,yo 第三步:写出曲顶柱体的表达式(利用对称性) 第四步:选择坐标系,确定积分区间 就是曲顶柱体的体积的负值, (1)区域边界应尽量多为坐标轴 (3)如果f(x,y)在D的若干部分是正的 (2)被积函数关于坐标变量易分离 在其余部分是负的,那么f(x,y)在 第五步:确定积分顺序,并计算 D上的二重积分等于xoy面上方的曲 (1)积分区域分块越少越好 顶柱体体积减去xOy面下方的曲顶柱 (2)类此积分容易出算出
一、 曲顶柱体体积的计算 回顾: 二重积分的几何意义 (1)如果 f x y ( , ) 0 ,二重积分 f x y d D ( , ) 就是曲顶柱体的体积 (2)如果 f x y ( , ) 0 ,二重积分 f x y d D ( , ) 就是曲顶柱体的体积的负值 (3)如果 f x y ( , )在 D 的若干部分是正的 在其余部分是负的 那么 f (x, y)在 D 上的二重积分等于 xoy面上方的曲 顶柱体体积减去 xoy面下方的曲顶柱 注记 1: 求曲顶柱体体积的一般步骤 第一步:画出曲顶柱体围成的几何草图 第二步:确定曲顶柱体的曲顶及区边表达式 第三步: 写出曲顶柱体的表达式(利用对称性) 第四步: 选择坐标系,确定积分区间 (1)区域边界应尽量多为坐标轴 (2)被积函数关于坐标变量易分离 第五步: 确定积分顺序,并计算 (1)积分区域分块越少越好 (2)类此积分容易出算出

例1求球体x2+y2+z2≤4a2被圆柱体x2+y2≤2ar的公共部分的体积. 分析:(1)画出几何草图 (3)写出曲顶柱体的表达式(利用对称性) 由对称性可知:所求立体的体积是 V=4到∬4a2-x2-y, (4)选择坐标系(极坐标),确定积分区间 该立体在第一卦限部分体积的4倍 x=pcoso 个2 (2)找出曲顶柱体的曲顶表达式及区边 将y=psinp 带入区边 由x2+y2+z2≤4a2可知z2≤4a2-x2-y2 表达式中可得 D:0≤p≤2 acosp, 由x2+y2≤2am可知y2≤2ar-x2 D 0≤p号 x2a 因此立体在第一卦限部分的曲顶为 (5)确定积分顺序并计算 =4a2-x2-y2 V=4∬V4a2-p2 pdpdo 因此立体在第一卦限部分的区边为 dod-ppdp D:y=\2ax-x2,y=0
例 1 求球体 2 2 2 2 x y z a 4 被圆柱体 2 2 x y ax 2 的公共部分的体积. 分析:(1)画出几何草图 x y z O 2a D 2a (2)找出曲顶柱体的曲顶表达式及区边 由对称性可知:所求立体的体积是 该立体在第一卦限部分体积的 4 倍 由 2 2 2 2 x y z a 4 可 知 2 2 2 2 z a x y 4 2 2 2 z a x y 4 因此立体在第一卦限部分的曲顶为 由 2 2 x y ax 2 可知 2 2 y ax x 2 因此立体在第一卦限部分的区 边为 2 D y ax x : 2 , y 0 (3)写出曲顶柱体的表达式(利用对称性) D V a x y dxdy 2 2 2 4 4 , (4)选择坐标系(极坐标),确定积分区间 将 cos sin x y 带入区边 D a : 0 2 cos , 表达式中可得 0 2 (5)确定积分顺序并计算 2 2 4 4 D V a d d 2 cos 2 2 2 0 0 4 4 a d a d

例2求x2+y2=R,x2+2=R所围成的立体的体积 解:(1)显然x2+y2=R,x2+2=R2所围成的立体关于三坐标面对称, 因此立体的体积是它在第一卦限部分体积的8倍 x2+z2=R2 (2)x2+y=R,x2+z2=R所围成的立体在第一卦限部分 可以看做是以:=√R2-x为曲顶的柱体 R D (3)显然:=√R2-x在XO少面上四分之一的投影是一个圆 X2+y2=R2 0≤y≤√R-x,0≤x≤R,所以x+y=R,x2+:2=R所围成的立体在第一卦限部分 的体积就是函数:=√R-x在闭区域D:0≤y≤VR2-,0≤x≤R上的二重积分 因此所求立体的体积 V-8R-do-dopR-
例 2 求 2 2 2 2 2 2 x y R x z R , 所围成的立体的体积 x y z O D x 2y 2R 2 x 2z 2R 2 R 解:(1)显然 2 2 2 2 2 2 x y R x z R , 所围成的立体关于三坐标面对称, 因此立体的体积是它在第一卦限部分体积的 8 倍 (2) 2 2 2 2 2 2 x y R x z R , 所围成的立体在第一卦限部分 可以看做是以 2 2 z R x 为曲顶的柱体 (3)显然 2 2 z R x 在 xoy 面上四分之一的投影是一个圆 2 2 0 , 0 y R x x R, 所以 2 2 2 2 2 2 x y R x z R , 所围成的立体在第一卦限部分 的体积就是函数 2 2 z R x 在闭区域 2 2 D y R x x R : 0 , 0 . 上的二重积分 因此所求立体的体积 2 2 8 D V R x d 2 2 2 2 0 0 8 R R x dx R x dy

二、曲面面积的计算 闭区域D的面积O公式 直角坐标系下 极坐标系下 o-川a-d a-f∬do-pdpde D:0(x)≤y≤p,(x),a≤x≤b D:a≤p≤B,p(p)≤p≤p(p) o=广=直a-a(ej达 -de ide D:Oy)≤x≤w,y),c≤y≤d D:a≤p≤B,0≤p≤p(p) a-=-%0 o=p”p-iIT]
闭区域 D的面积 公式 直角坐标系下 极坐标系下 D D d dxdy D D d d d 1 2 D x y x a x b : ( ) ( ), 2 1 ( ) 2 1 ( ) ( ) ( ) b x b a x a dx dy x x dx 1 2 D: , ( ) ( ) 2 1 ( ) 2 2 2 1 ( ) 1 ( ) ( ) 2 d d d 1 2 D y x y c y d : ( ) ( ), 2 1 ( ) 2 1 ( ) ( ) ( ) d y c y dy dx y y dy D: , 0 ( ) ( ) 2 0 1 ( ) 2 d d d 二、 曲面面积的计算
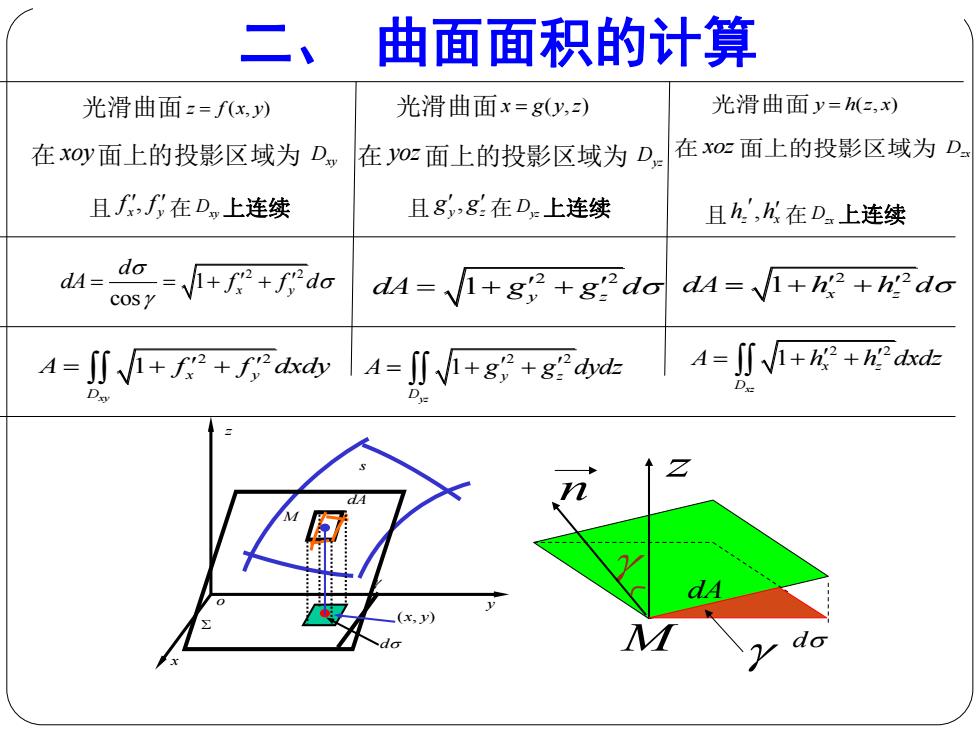
二 、曲面面积的计算 光滑曲面z=x,) 光滑曲面x=g(y,) 光滑曲面y=h(z,x) 在xoy面上的投影区域为D, 在or面上的投影区域为D,在oc面上的投影区域为D 且f,f在D,上连续 且8,8:在D,上连续 且h.',以在D上连续 dA=do ++da cosy dA=1+g3 +g.do dA=++h"do A=J∬V+f2+FcdA=j∬V+g+gk A=V+2+正 D dA x,y) do
二、 曲面面积的计算 光滑曲面 z f (x, y) 在 xoy面上的投影区域为 D xy 光滑曲面 x g(y,z) 在 yoz面上的投影区域为 D yz 光滑曲面 y h(z, x) 在 xoz 面上的投影区域为 D zx 且 , x y f f 在D xy 上连续 且 , y z g g 在D yz 上连续 且 , z x h h 在D zx 上连续 d (x, y) M dA x y z s o M dA z d n 2 2 1 cos x y d dA f f d 2 2 dA g g d 1 y z 2 2 dA h h d 1 x z 2 2 1 xy x y D A f f dxdy 2 2 1 yz y z D A g g dydz 2 2 1 xz x z D A h h dxdz

二、 曲面面积的计算 回顾: 光滑曲面z=f(x,y)在Oy面 第三步:确定曲面在坐标面上的投D。 上的投影区域为D. 第四步:求出偏导数 则该曲面的面积为. 第五步:代入曲面面积公式式 A=S5++dxdy D A=j∬+f+fdk D 注记2:求曲面面积的一般步骤 第六步:选择坐标系,确定积分区间 第一步:画出几何草图(利用对称性) 第七步:确定积分顺序,并计算 第二步:确定曲面表达式:=fx,)
二、 曲面面积的计算 回顾: 光滑曲面z f x y ( , )在 xoy 面 上的投影区域为 D xy 则该曲面的面积为 2 2 1 xy x y D A f f dxdy 注记 2: 求曲面面积的一般步骤 第四步:求出偏导数 第五步: 代入曲面面积公式式 第六步: 选择坐标系,确定积分区间 第七步: 确定积分顺序,并计算 第一步:画出几何草图(利用对称性) 第二步:确定曲面表达式z f x y ( , ) 第三步:确定曲面在坐标面上的投 D xy 2 2 1 xy x y D A f f dxdy

二 曲面面积的计算 例3求球面x2+y2+z2=ad2的表面积 在D,的边界:x2+y2=ad上不连续 分析(1)球面x2+y+2=a分为上下两 因此不能直接使用公式 半球面,由对称性可知所求的表 (4) 取闭区域D:x2+y≤b(0<b<为积分区域 面积是上球面的表面积的2倍 0z0z 显然x'在D上连续 (2)写出上球面的方程:=√层-x2- 则闭区域D上上半球面的表面积 及它在xOy上的投影Dm:x2+y2≤a 4-后 (3)求出x Va2-x2-y2' Va2-x2-y 则闭区域D上球面的表面积 0z 0z 判断ax'在D,r+y≤d上是否连续 4=2 lim 4
二、 曲面面积的计算 例 3 求球面 2 2 2 2 x y z a 的表面积 分析(1)球面 2 2 2 2 x y z a 分为上下两 半球面,由对称性可知所求的表 面积是上球面的表面积的 2 倍 (2)写出上球面的方程 2 2 2 z a x y 及它在 xoy 上的投影D xy 2 2 2 : x y a (3)求出 2 2 2 2 2 2 , z x z y x y a x y a x y 判断 , z z x y 在D xy 2 2 2 : x y a 上是否连续 在D xy 的边界 2 2 2 : x y a 上不连续. 因此不能直接使用公式 (4) 取闭区域 D1 : 222 x y b b a (0 ) 为积分区域 显然 , z z x y 在D1 上连续 则闭区域 D1 上上半球面的表面积 1 1 2 2 1 2 2 2 1 x y D D a A z z dxdy dxdy a x y 则闭区域 D xy 上球面的表面积 1 2 lim b a A A